Оценка погрешностей электрических измерений
Абсолютная погрешность измерений, производимых электроизмерительными приборами, оценивается исходя из класса точности приборов. Обозначение класса точности 0,2; 0,5; 1,0 2,0 и т. д. не только характеризует прибор в зависимости от системы, конструкции, качества материалов, точности градуировки и других факторов, но и указывает, что погрешность показаний прибора соответствующего класса в любом месте шкалы не должна превышать 0,2%; 0,5%; 1, 2 %.
Если обозначим через А'максимально возможное показание прибора, а через n номер класса прибора, то получим абсолютную погрешность прибора
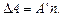
Например, вольтметр 0,2 класса (n — 0,002), шкала которого рассчитана на 5 В, имеет абсолютную погрешность:
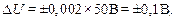
а амперметр класса 1,5, рассчитанный на максимальное показание 5 А, имеет абсолютную погрешность:
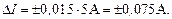
Так как абсолютная погрешность считается одинаковой по всей шкале данного электроизмерительного прибора, то относительная погрешность 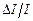 будет тем больше, чем меньше измеряемая величина. Например, если при помощи указанного амперметра измерить ток 4А, то относительная погрешность будет составлять 1,9 %, а при измерении силы тока 1А - 7,5 %.
будет тем больше, чем меньше измеряемая величина. Например, если при помощи указанного амперметра измерить ток 4А, то относительная погрешность будет составлять 1,9 %, а при измерении силы тока 1А - 7,5 %.
При точных измерениях следует пользоваться такими приборами, чтобы предполагаемое значение измеряемой величины составляло 70 - 80 % от максимального (номинального) значения. Поэтому применяют приборы, имеющие несколько пределов измерений; при работе с таким прибором его включают и цепь на тот предел измерений, который достаточно близок к предполагаемому значению измеряемой величины.
Вычислим погрешности на примере измерения внутреннего сопротивления элемента, электродвижущая сила которого 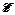 ,напряжение на полюсах U и величина тока в цепи I. Измерения проведены: вольтметром класса 0,5 (UN = 2,5 В) и амперметром класса 1,0 (IN = 1,5 А). Результаты измерений следующие:
,напряжение на полюсах U и величина тока в цепи I. Измерения проведены: вольтметром класса 0,5 (UN = 2,5 В) и амперметром класса 1,0 (IN = 1,5 А). Результаты измерений следующие:
E = 2 В, U = 1,3 В, I = 1,2 А.
Абсолютные погрешности измерений:
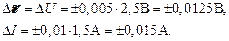
Внутреннее сопротивление определим из закона Ома для полной цепи:

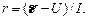
Прологарифмируем выражение (1)
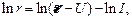
затем продифференцируем его, заменив d на 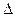 и знаки "-" на знаки "+" найдем относительную погрешность ε:
и знаки "-" на знаки "+" найдем относительную погрешность ε:
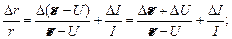
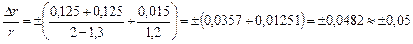 Эта погрешность, выраженная в процентах, составляет:
Эта погрешность, выраженная в процентах, составляет:
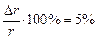
С помощью формулы (1) находим внутреннее сопротивление r и абсолютную погрешность 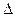 r:
r:
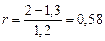 Ом
Ом
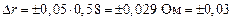 Ом.
Ом.
В практике физического эксперимента при количественных определениях физических величин сталкиваемся с необходимостью обработки полученных результатов.
Осуществление каждого измерения или отсчета влечет за собой появление ошибок (или погрешностей), зависящих от различных причин. Поэтому при измерении всякой физической величины перед экспериментатором стоят две задачи:
1) произвести измерение физической величины с возможно меньшим отклонением полученного результата от ее истинного значения;
2) дать оценку погрешности, полученной при этом измерении.
Так, измеряя удельное сопротивление материала образца, мы должны не просто указать его величину, равную, например, 10 Ом  см, а с учетом погрешностей измерений ± 0,1 %, записать:
см, а с учетом погрешностей измерений ± 0,1 %, записать:
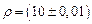 Ом
Ом  см.
см.
Измерения бывают:
1) прямые (или непосредственные), когда на шкале прибора сразу виден отсчет измеряемой величины;
2) косвенные, когда интересующая величина вычисляется по формуле с помощью других, доступных непосредственному физическому измерению величин.
К непосредственным измерениям относятся измерения линейных размеров образцов, измерения температуры, измерения ряда величин с помощью специальных приборов (непосредственный отсчет по шкале). Ошибки, возникающие в процессе измерения физических величин, разделяются на два класса:
1. Систематические ошибки, связанные с несовершенством измерительных приборов, с неправильной их установкой или использованием. К числу таких ошибок могут быть отнесены ошибки, возникающие вследствие смещения нулевой точки шкалы термометра или электроизмерительного прибора, изменения показания термопары в результате непостоянства температуры холодного конца (если он специально не термостатирован, а имеет температуру окружающей среды), изменение сопротивления подводящих проводов с температурой и т. д.
Систематические ошибки имеют при данных условиях всегда один и тот же знак, они изменяют измеряемую величину в одну и ту же сторону и устраняются путем тщательной регулировки, правильной установки приборов или путем введения специальных поправок.
2. Случайные ошибки - являются результатом влияния случайных факторов, неподдающихся предварительному учету. Случайные ошибки могут иметь разные знаки и способны как увеличивать, так и уменьшать получаемый результат. При наличии достаточно большого числа измерений случайные ошибки подчиняются статистическим закономерностям. Учет и оценка случайных ошибок составляют специальную главу теории вероятности, называемую "теорией ошибок".
В теории ошибок доказывается, что наиболее достоверным значением измеряемой величины является среднее арифметическое из результатов отдельных измерений, так как положительные и отрицательные случайные ошибки, равные по абсолютной величине, в среднем встречаются одинаково часто.
Если измеряется некоторая физическая величина a и произведено n измерений, в результате которых получены значения a1, a2, a3,..., an,то наиболее достоверное значение измеряемой физической величины a0 равно среднему арифметическому a0:
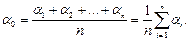
Разность между результатом отдельного измерения и средним арифметическим
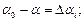
представляет абсолютную ошибку отдельного измерения. Эти ошибки могут иметь как положительное, так и отрицательное значение.
Средней абсолютной ошибкой измерения называют:
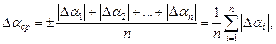
среднее арифметическое из абсолютных значений отдельных измерений.
В теории ошибок вводятся также понятия средней квадратичной и средней вероятной ошибки 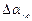 и
и 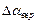 :
:
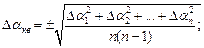
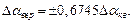
Окончательный результат записывается так:
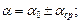
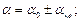
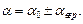
Для того, чтобы охарактеризовать точность измерений определяют относительную ошибку, равную отношению абсолютной ошибки к измеряемой величине. Эта ошибка может быть выражена в процентах. Так же определяют среднюю, среднюю квадратичную и среднюю вероятную относительные ошибки:
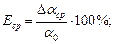
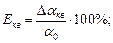
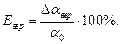
В теории ошибок доказывается, что значения случайных ошибок подчинены нормальному закону распределения, т. е. чем больше отклонение величины от ее наиболее вероятного значения, тем реже оно встречается. Поэтому, проведя целую серию измерений, можно увеличить точность полученного среднего значения измеряемой величины (табл. 2).
В качестве примера приведем результаты измерении толщины образца с помощью микрометра. Точность подобных измерений является определяющей при вычислении целого ряда величин: плотности, электропроводности и т.д.
Таблица 2
| Номер измерений | d, мм | 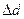 , мм , мм | 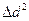 |
| 2,32 | +0,02 | 0,0004 | |
| 2,34 | 0,00 | 0,0000 | |
| 2,36 | -0,01 | 0,0004 | |
| 2,33 | +0,01 | 0,0001 | |
| 2,35 | -0,01 | 0,0001 | |
| 2,33 | +0,01 | 0,0001 | |
| 2,32 | +0,02 | 0,0004 | |
| 2,24 | 0,00 | 0,0000 | |
| 2,33 | +0,01 | 0,0001 | |
| 2,35 | -0,01 | 0,0001 |
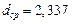 мм;
мм; 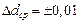 мм;
мм;
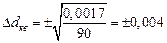 мм;
мм;
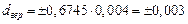 мм.
мм.
Соответственно относительные ошибки и окончательный результат:
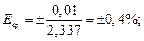
 мм,
мм,
или округляя: 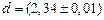 мм, чтобы абсолютная величина меняла последний знак результата:
мм, чтобы абсолютная величина меняла последний знак результата:
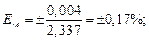
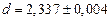 мм
мм
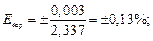
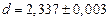 мм.
мм.
При количестве измерений меньшем десяти вычислять квадратичную и вероятную ошибку нельзя.
Во многих случаях лабораторных измерений приходится ограничиваться однократным измерением. Тогда абсолютные ошибки измерений оценивают по точности измерительных приборов.
Для электроизмерительных приборов класс точности указывается особо. Так как половину наименьшего деления шкалы еще можно оценить на глаз, то максимальная ошибка измерения принимается равной этой величине. Так, например, при отсутствии особых указаний в паспорте прибора, абсолютную ошибку термометра с наименьшей ценой деления в 1° принимают за 0,5°, микрометра с наименьшей ценой деления в 0,01 мм – за 0,005 мм и т. д.
Приведем для наглядности два примера:
1 пример. Ток величиной около 10 мА измеряется многопредельным амперметром М 104 с классом точности 0,5 на разных диапазонах.
В табл. 3 приведены значения абсолютных и относительных ошибок при измерениях на разных диапазонах.
Таблица 3
| Диапазон | Абсолютная ошибка | Запись результатов | Относительная ошибка |
| 0,015 А 15 мА | 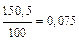 мА мА | (10 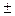 0,075) мА 0,075) мА | 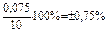 |
| 0,03 А 30 мА | 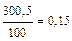 мА мА | (10 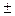 0,15) мА 0,15) мА | 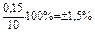 |
| 0,075 А 75 мА | 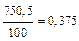 мА мА | (10 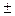 0,375) мА 0,375) мА | 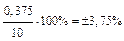 |
| 0,15 А 150 мА | 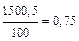 мА мА | (10 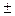 0,75) мА 0,75) мА | 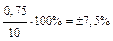 |
| 0,3 А 300 мА | 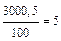 мА мА | (10 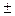 1,5) мА 1,5) мА | 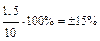 |
2 пример. С помощью амперметра со шкалой 0 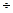 100 А производится измерение силы тока. Класс точности прибора 1,0. Абсолютная ошибка постоянная:
100 А производится измерение силы тока. Класс точности прибора 1,0. Абсолютная ошибка постоянная: 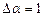 А.
А.
В табл. 4 приведены значения некоторых измеряемых величин, произведённых с помощью этого прибора с указанием абсолютной и относительной ошибок.
Таблица 4
| Показание, А | Запись, А | Относительная ошибка, % |
5 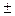 1 1 | 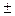 20 20 | |
10 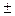 1 1 | 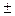 10 10 | |
23 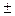 1 1 | 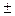 4 4 | |
50 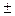 1 1 | 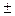 2 2 | |
75 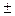 1 1 | 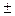 1,33 1,33 | |
100 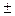 1 1 | 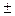 1 1 |
Очевидно, что при ответственных измерениях надо так подбирать шкалу измерительного прибора (на многопредельных приборах) или, соответственно, подбирать такой прибор, чтобы показания лежали во второй (большей) половине шкалы. У приборов с неоднородной шкалой рабочая часть шкалы начинается от 25 % номинального предела измерений.
Примечание: При работе на второй половине шкалы легко (в случае некоторой неосторожности) получить зашкаливание прибора, что ведет к его порче. Поэтому сначала рекомендуется проверить измеряемую величину на шкале, пределы которой значительно превышают ожидаемую величину, а затем менять диапазон.
Приведенная погрешность прибора (выражаемая в процентах) определяет класс точности прибора.
Существуют приборы следующих классов: 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0- с приведенными погрешностями, соответственно: ± 0,1 %; ± 0,2 %; ± 0,5 %; ± 1,0 %; ± 1,5 %; ± 2,5 %; ± 4,0 %.
Для приборов с односторонней шкалой (нуль слева) приведенная погрешность будет определяться по отношению к верхнему пределу измерений.
При двусторонней шкале (нуль посередине) за максимальное значение показаний принимается сумма абсолютных значений верхнего и нижнего предела измерений, а в случае отсутствия нуля на шкале в качестве максимального значения принимается разность между верхним и нижним пределом.
Для стрелочных гальванометров обычно указывается цена одного деления, так называемая постоянная гальванометра. Например, у гальванометра М-91 (А постоянная по току равна 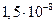 А/деление).
А/деление).
