Непрерывная случайная величина

Числовые характеристики непрерывной случайной величины (н.с.в.). Дискретная случайная величина может принимать значения некоторой числовой последовательности – конечной или бесконечной. Дискретность случайной величины, принимающей эти значения, будет состоять в том, что между любыми значениями 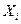и будет только конечное число членов этой последовательности, и в случае необходимости можно все эти промежуточные значения записать.

Поэтому закон распределения дискретной случайной величины можно задать в виде таблицы, в которой по порядку перечислены все или сколько угодно много возможных значений этой случайной величины.

Определение 14.1. Случайная величина, которая может принимать любое действительное значение на некотором промежутке или на всей числовой оси, называется непрерывной случайной величиной.

Исходя из определения н.с.в., которая принимает все конкретные значения некоторого числового промежутка реальных чисел, причем между любыми двумя такими значениям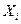и и имеется бесконечно много чисел, и все эти числа записать невозможно, как не пытаться. Например, эти числа нельзя пронумеровать, между любыми из них опять существует бесконечно много чисел.

Таким образом процесс нумерования окажется бесконечным, а это и обуславливает отсутствие возможности закон распределения непрерывной случайной величины представить в виде таблицы, которая применяется в случае дискретной случайной величины.

Пример 14.1. При вытачивании на станке детали цилиндрической формы ее диаметр принимает значения от 1,45 см до 1,55 см, то есть . Значит, может принять любое значение на отрезке и является непрерывной случайной величиной.

Функция распределения случайной величины. Закон распределения непрерывной случайной величины нельзя задать таблицей. В этом случае рассматривают событие , где 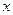– заданное действительное число. 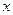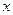Поскольку каждому значению соответствует один и только один промежуток , а каждому такому промежутку – одно и только одно событие вероятность которого , то есть вероятность того, что значение величины будет меньше числа , то выходит, что каждому значению 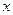соответствует одно и только одно значение . Значит, между 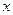и существует функциональная зависимость, которую обозначим 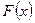, т.е. .

Определение 14.2. Функцией распределения или интегральной функцией распределения непрерывной случайной величины называется вероятность того, что примет значение меньше 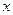, то есть .

Определение 14.3.Интегральной функцией распределения или функцией распределения случайной величины называется вероятность события { } , состоящего в том, что случайная величина примет значение, меньшее 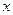, т.е.

.

Геометрически это равенство определяет вероятность попадания случайной величины левее точки 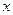, т.е. в интервал .

В дальнейшем под непрерывной случайной величиной будем понимать такую случайную величину , для которой интегральная функция распределения 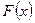непрерывна и дифференцируема на всей числовой оси .

Свойства функции распределения 1. 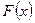– неубывающая функция.

В самом деле, пусть . Тогда событие представляет собой объединение двух событий: и . Так как эти события несовместны, то

.

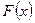Поскольку , то т.е. и Значит, функция – неубывающая.

2. .

Это свойство вытекает из определения, так как .

3.

Событие достоверное, поэтому .

4. .

Событие невозможное, поэтому .

Замечание 1.Когда известно, что случайная величина может принимать только значения промежутка , то достоверным событием является событие « », а невозможным – « ». В таком случае:

5. Если известна функция распределения ,товероятность попадания случайной величины на заданный интервал равна приращению функции распределения на этом интервале:

.

Рассмотрим события « » и « ». Эти события несовместны, тогда

, т.е.

.

Пример 14.2. Функция распределения случайной величины имеет вид

Найти вероятность того, что в результате испытания примет значение, заключенное в промежутке .

График функции F( x ) имеет вид (рис. 14.1):

Рис. 14.1

.

Ответ:

Замечание. Так как , то

,

то есть вероятности попадания значения величины в замкнутый или открытый интервал одинаковы.

Замечание. Интегральную функцию распределения можно составить и для дискретной случайной величины

,

но эта функция является разрывной.

Пусть задана функция

Изобразим график этой функции (рис. 14.2).

Рис. 14.2

Дифференциальная функция распределения непрерывной случайной величины или плотность распределения.Рассмотрим интегральную функцию распределения . Вероятность

Из курса элементарной математики известно, что

.

Действительно, – это доля вероятности , соответствующая единице измерения длины отрезка , то есть плотность этой вероятности на . Тогда плотность этой вероятности в точке будет равна

.

Для произвольной точки 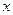имеем

Определение 14.4. Функцией плотности вероятностей или дифференциальной функцией распределения непрерывной случайной величины 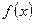называется производная интегральной функции распределения 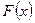, т.е.

Значит, функция распределения 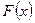представляет собой первообразную от функции плотности вероятностей .

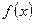Свойства дифференциальной функции 1. Это следует из определения 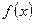как производной от неубывающей функции .

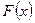2. .

По формуле Ньютона – Лейбница имеем

.

Геометрически (рис. 14.3) вероятность попадания непрерывной случайной величины в интервал представляет собой площадь криволинейной трапеции, ограниченной графиком функции плотности вероятностей , осью 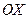и двумя прямыми и

Рис. 14.3

3.

Если все возможные значения 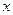принадлежат промежутку , то событие « » – есть достоверное событие, и поэтому .

4. ,

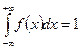то есть площадь, ограниченная кривой плотности и осью 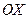при всех значениях, которые может принимать случайная величина , равна единице.

5. , т.к. .

6. .

Очевидно, и .

Замечание. В большинстве задач теории вероятностей закон распределения непрерывной случайной величины задается дифференциальной функцией распределения (функцией плотности) .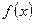

Пример 14.3. Плотность распределения случайной величины имеет вид

Найти вероятность того, что .

График функции 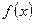имеет вид (рис. 14.4).

Рис. 14.4

Ответ:

Числовые характеристики непрывной случайной величины.Пусть непрерывная случайная величина распределена на промежутке с плотностью распределения : вне промежутка .

Определение 14.5. Математическим ожиданием непрерывной случайной величины называется число 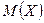, равное определенному интегралу

,

если он существует:

.

Если область распределения случайной величины не указана, то

,

если эти пределы существуют.

Определение 14.6. Дисперсией непрерывной случайной величины называется число, равное

,

или

,

если эти интегралы существуют.

Если область возможных значений случайной величины не указана, то

или

,

если эти интегралы существуют.

Определение 14.7. Средним квадратическим отклонением случайной величины называется число

Пример14.4. Случайная величина распределена на промежутке с плотностью распределения . Найти .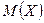

Ответ. .

Пример 14.5. Дифференциальная функция распределения случайной величины имеет вид

Найти дисперсию и среднее квадратическое отклонение непрерывной случайной величины .

.

Ответ.

Мода и медиана случайной величины.Кроме математического ожидания и дисперсии в теории вероятностей применяются еще и другие числовые характеристики случайной величины, которые отражают те или иные особенности распределения этой случайной величины.

Определение 14.8. Модой случайной величины называется ее наиболее вероятное значение, т.е. значение, для которого вероятность или плотность распределения 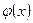достигает максимума и обозначается .

Определение 14.9. Медианой случайной величины называется такое ее значение, для которого выполняется равенство:

Геометрически прямая , перпендикулярная оси 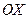, делит площадь фигуры под кривой распределения на две равные части:

Определение 14.10. Начальным моментом к-го порядка случайной величины называется математическое ожидание к-й степени этой величины и обозначается через , то есть

для дискретной случайной величины

а для непрерывной случайной величины

Определение 14.11. Центральным моментом к -го порядка случайной величины называется математическое ожидание к-ой степени отклонения случайной величины от ее математического ожидания и обозначается

или

, где .

Тогда для дискретной случайной величины имеем

а для непрерывной случайной величины получим

В том числе, при к =1 первый начальный момент случайной величины есть ее математическое ожидание, т.е.

;

при к = 2 второй центральный момент

есть дисперсия случайной величины .

Математическое ожидание или первый начальный момент характеризует среднее значение случайной величины или положение распределения случайной величины . Дисперсия 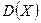или второй центральный момент характеризует степень рассеяния распределения относительно ее или меру разброса значений случайной величины относительно ее среднего значения .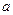

Определение 14.12.Коэффициентом асимметрии случайной величины называется отношение третьего центрального момента к кубу среднего квадратического отклонения и обозначается .

Третий центральный момент характеризует асимметрию или скошенность распределения случайной величины . Если , то распределение симметрично относительно .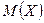

Рис. 14.5

На рисунке 14.5 показаны две кривые распределения I и II. Кривая I имеет положительную (правостороннюю) асимметрию а кривая II – отрицательную (левостороннюю)

Определение 14.13. Эксцессом случайной величины называется число равное отношению четвертого центрального момента к четвертой степени среднего квадратического отклонения минус 3, и обозначается

.

Четвертый центральный момент характеризует крутость распределения, т.е островершинность или плосковершинность кривой. Для нормальной кривой , т.е. (рис. 14.6, кривая II).

Рис. 14.6

Более островершинная кривая имеет (рис. 14.6, кривая I), более плосковершинная кривая имеет (рис. 14.6, кривая III).