Лекция 4. Математические понятия и методика их формирования.
План:
1. Понятие как форма мышления. Содержание и объем понятия.
2. Определение понятия, виды определений. Классификация понятий.
3. Методика изучения понятий в курсе средней школы (пропедевтика, введение, усвоение, закрепление, предупреждение ошибок).
.
1.Познание окружающего мира осуществляется в диалектическом единстве чувственной и рациональной форм мышления. К чувственным формам мышления относятся: ощущение, восприятие, представление. К рациональным формам мышления относятся: понятия, суждения, умозаключения. Ощущение и восприятие—первые сигналы действительности. На их основе образуются общие представления, а от них в результате сложной умственной деятельности мы переходим к понятиям.
Понятие — это форма мышления, в которой отражаются существенные признаки (свойства) объектов реального мира.
Свойство является существенным, если оно присуще этому объекту и без него оно не может существовать. Например, формальное понятие куба (различные кубы, размеры, цвета, материалы). При наблюдении их возникает восприятие объекта, следовательно, возникает представление об этих объектах в сознании. Затем, выделяя существенные признаки, формируется понятие.
Итак, понятие абстрагируется от индивидуальных черт и признаков отдельных восприятий и представлений, и является результатом обобщения восприятий и представлений очень большого количества однородных явлений и предметов.
Всякое понятие имеет две логические характеристики: содержание и объем.
Содержанием понятия называется совокупность существенных, взаимосвязанных признаков (свойств) объекта.
Объемом понятия называется совокупность объектов, обозначаемых одним и тем же термином (названием).
Например, термин (название) — трапеция.
Содержание понятия:
1) четырехугольник,
2) одна пара противолежащих сторон параллельна,
3) другая пара противолежащих сторон не параллельна,
4) сумма углов прилежащих к боковой стороне равна 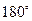 .
.
Объем понятия – все мыслимые трапеции.
Между содержанием понятия и объемом существует следующая связь: чем больше объем понятия, тем меньше его содержание, и наоборот. Так, например, объем понятия «равнобедренный треугольник» меньше объема понятия «треугольник». А содержание первого понятия больше содержания второго, ибо равнобедренный треугольник обладает не только всеми свойствами треугольника, но и особыми свойствами присущими только равнобедренным треугольникам (боковые стороны равны, углы при основании равны). Итак, если увеличить содержание, то уменьшится объем понятия.
Если объем одного понятия входит как часть в объем другого понятия, то первое понятие называют видовым, а второе родовым.
Например, ромб—это параллелограмм, у которого все стороны равны (Погорелов, 8 класс). Ромб - видовое, параллелограмм - родовое.
Квадрат—это прямоугольник, у которого все стороны равны (Погорелов, 8 класс). Квадрат - видовое, прямоугольник - родовое.
Но, квадрат—это ромб, у которого угол прямой.
То есть понятие рода и вида относительны.
Каждое понятие связано со словом-термином, которое соответствует данному понятию. В математике понятие часто обозначается символом (  ║). Термины и символы — это средства, которые служат для выражения и фиксирования математических понятий, для передачи и обработки информации о них.
║). Термины и символы — это средства, которые служат для выражения и фиксирования математических понятий, для передачи и обработки информации о них.
2. В содержание понятия о каком-либо математическом объекте входит много различных существенных свойств этого объекта. Однако чтобы распознать объект, установить принадлежит ли он к данному понятию или нет, достаточно проверить наличие у него некоторых существенных свойств.
Определение понятия — формулировка предложения, в котором перечисляются необходимые и достаточные признаки понятия. Таким образом, содержание понятия раскрывается через определение.
Виды определений понятий.
1.Определение через ближайший род и видовое отличие.

Подчеркнем, что в качестве видового отличия всегда берется несущественный признак родового понятия, который для определяемого понятия является уже существенным.
|
|
 |
Свойства объекта в таком определении раскрываются путем показа операций его конструирования.
Пример, треугольники называются равными, если у них соответствующие стороны и соответствующие углы равны (Погорелов, 7 класс). Это определение подсказывает учащимся, как построить треугольник равный данному.
3.Определения - условные соглашения. Те же конструктивные определения, но основанные на некотором соглашении. Такие определения используются в школьном курсе математики при расширении понятия числа.
Например, 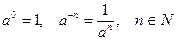 .
.
4. Индуктивные (рекурсивные). Указываются некоторые базисные объекты некоторого класса и правила, позволяющие получить новые объекты этого же класса.
Например. Числовая последовательность каждый член, которой, начиная со второго, равен предшествующему члену, сложенному с одним и тем же числом, называется арифметической прогрессией.
5. Отрицательные определения. Они не задают свойства объекта. Они выполняют как бы классификационную функцию. Например, скрещивающиеся прямые — это такие прямые, которые не принадлежат плоскости и не пересекаются.
6. Аксиоматическое определение. Определение через систему аксиом. Например, определение площади и объема.
Виды ошибок при определении понятий.
1) Определение должно быть соразмерно - в нём должно быть указано ближайшее родовое понятие к определяемому понятию (параллелограмм—это четырехугольник, параллелограмм—это многоугольник).
2) Определение не должно содержать «порочного круга» — первое определяется через второе, а второе через первое ( прямой угол равен девяносто градусов, один градус—это одна девяностая прямого угла).
3) Определение должно быть достаточным. В определении должны быть указаны все признаки, позволяющие однозначно выделить объекты определяемого понятия (смежными называются углы, которые в сумме дают 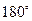 ).
).
4) Определение не должно быть избыточным, то есть в определении не должно быть указано лишних признаков определяемого понятия. Например, ромб—это параллелограмм, у которого все стороны равны (Погорелов, 8 класс). Это определение избыточно, ибо достаточно равенства двух смежных сторон.
5) Определение не должно быть тавтологией, то есть повторяющей в любой словесной форме ранее сказанное. Например, равными треугольниками называются треугольники, которые равны между собой.
Логическая структура видовых отличий.
1. Видовые отличия могут быть связаны союзом «и» — конъюнктивная структура определения.
2. Видовые отличия связаны союзом «или» — дизъюнктивная структура определения.
3. Видовые отличия связаны словами «если…., то …» — импликативная структура.
Если с содержанием понятия связано определение, то с объемом связана классификация.
Классификация – это распределение объектов какого-либо понятия на взаимосвязанные классы (виды, типы) по наиболее существенным признакам (свойствам). Признак (свойство), по которому происходит классификация (деление) понятия на виды (классы), называется основанием классификации.
При проведении классификации необходимо соблюдать следующие правила:
1) В качестве основания классификации можно брать лишь один общий признак всех объектов данного понятия, он должен оставаться неизменным в процессе классификации.
2) Каждый объект понятия должен попасть в результате классификации в один и только один класс.
3) Классификация должна быть соразмерной, то есть объединение классов объектов составляют объем понятия (нет объекта, который не попал бы ни в один класс).
4) Классификация должна быть непрерывной, то есть в процессе классификации необходимо переходить к ближайшему (к данному) родовому понятию (виду).
В настоящее время в школьных учебниках термин классификация не употребляется, требования не указываются. Но это не значит, что учитель не классифицирует понятия. Классифицировать можно числа, функции, алгебраические выражения, геометрические преобразования, многоугольники, многогранники. Её можно оформлять в виде схемы, таблицы.
Учащихся следует подготавливать к построению классификации постоянно. На первом этапе учащимся следует предлагать готовые схемы, таблицы. На втором заполнение этих схем, таблиц. На третьем самостоятельное конструирование.
Виды классификаций:
1. Классификация по видоизмененному признаку. Например, треугольник. Основание классификации: величина внутренних углов, члены: прямоугольные, остроугольные, тупоугольные.
2. Дихотомическая классификация (dicha и tome(греч)- «сечение на две части»). Оно представляет собой деление объема классифицируемого понятия на два противоречащих друг другу видовых понятия, одно из которых обладает данным признаком, а другое не обладает им.
Например, 
3. При формировании понятия следует соблюдать три этапа: введение, усвоение, закрепление.
I. Введение может осуществляться двумя путями:
а) конкретно-индуктивный—все признаки понятия рассматриваются на примерах или задачах, после чего вводится термин и определение.
б) абстрактно-дедуктивным—сразу дается определение, а потом на примерах обрабатываются признаки.
II. Усвоение.
Здесь прослеживаются две цели:
1) выучить определение.
2) Научить учащихся определять подходит ли объект под рассматриваемые понятия или нет. Этот этап осуществляется на специально составленных упражнениях.
Для реализации второй цели необходимо:
1) указывать систему необходимых и достаточных свойств объектов данного класса.
2) установить, обладает данный объект выделенными свойствами или нет.
3) заключить о принадлежности объекта к данному понятию.
III. Закрепление—решение более сложных задач, включающих рассматриваемые понятия.
Замечание 1. Формулируя определение понятия, следует обратить внимание на то, понятен ли учащимся смысл каждого слова, используемого в определении. В первую очередь следует обращать внимание на следующие слова: «каждый», «не более» и т.д.
Замечание 2. На этапе закрепления понятия следует предлагать задания не только на распознавание объекта, но и на отыскание следствий. Например, известно, что четырехугольник 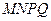 - трапеция (
- трапеция ( 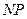 и
и 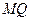 её основания). Назовите следствия, вытекающие из данных условий в силу определения трапеции.
её основания). Назовите следствия, вытекающие из данных условий в силу определения трапеции.
Необходимы комплексные упражнения, выполнение которых основано только на использовании существенных свойств понятия, но и на отыскании следствий.
Например. Известно, что некоторый луч исходит из вершины угла. Следует ли отсюда, что этот луч является биссектрисой угла? Если нет, то измените, условие так, чтобы из него следовало, что луч являлся бы биссектрисой данного угла.
Замечание 3. Многие определения в ШКМ содержат знаки существования и общности (первообразная, четная функция, периодическая функция и т.д.). Работа по усвоению таких определений обладает некоторой специфичностью.
Пример. Функция f называется четной, если для любого x из её области определения f(-x)=f(x), причем область определения симметрична относительно начала координат, то есть для любого x из области определения число (-x)также принадлежит области определения. (f четна на М) 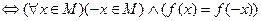 .
.
Из этого определения можно получить условие непринадлежности функции к понятию четной функции, которое можно записать так:
(f не являетсячетной на М) 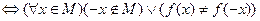 .
.
Теперь можно подобрать систему упражнений на усвоение данного понятия:
1) Является ли функция f четной на множестве М, если:
А) для любого 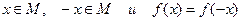 .
.
В) существует такой 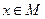 , что
, что 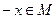 , а
, а 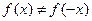 .
.
С) существует такой 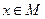 , что
, что 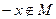 , а
, а 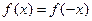 ?
?
2) Известно, что функция h является четной на множестве М. Что от сюда следует?
3) Известно, что существует такой 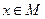 , что
, что 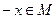 и
и 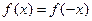 . Можно ли утверждать, что функция является четной на множестве М? Если нет, то измените, условие так, чтобы из него следовало, что функция f была бы четной на М.
. Можно ли утверждать, что функция является четной на множестве М? Если нет, то измените, условие так, чтобы из него следовало, что функция f была бы четной на М.
