Расчет сложных цепей при помощи уравнений Кирхгофа
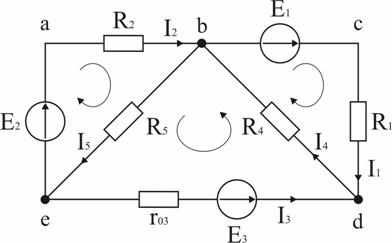
Задача 2. Рассчитать схему рис. 1.30, составив систему уравнений на основании законов Кирхгофа.
Исходные данные к задаче:
E1 = 60 В; E2 = 80 В; E3 = 70 В;
R1 = 20 Ом; R2 = 50 Ом; r03 = 5 Ом; R4 = 65 Ом; R5 = 85 Ом.
Анализ и решение задачи 2
1. Определение необходимого числа уравнений.
В схеме рис. 1.30 пять ветвей и для расчета токов в них надо составить пять уравнений. По первому закону Кирхгофа составляются уравнения для всех узлов, кроме одного (уравнение для него будет следствием предыдущих), по второму – для независимых контуров (в каждый последующий контур входит хотя бы одна ветвь, не вошедшая в ранее рассмотренные). Для данной схемы надо составить два уравнения по первому закону и три – по второму.
2. Составление и решение системы уравнений.
Для составления уравнений задаемся произвольно направлениями токов в ветвях и направлениями обхода контуров (рис. 1.30).
Уравнение для узла d: I1 + I3 - I4 = 0.
Уравнение для узла е: - I2 - I3 + I5 = 0.
Уравнение для контура bcd: I1R1 + I4R4 = E1.
Уравнение для контура abe: I2R2 + I5R5 = E2.
Уравнение для контура bde: I3r03 + I4 R4 + I5R5 = E3.
Подставив в уравнения численные значения величин, получим алгебраическую систему уравнений:
I1 + I3 - I4 = 0;
- I2 - I3 + I5 = 0;
20 I1 + 65 I4 = 60;
50 I2 + 85 I5 = 80;
5 I3 + 65 I4 + 85 I5 = 70.
Решение системы дает значения токов: I1 = 1,093 А; I2 = 0,911 А; I3 = –0,506 А; I4 = 0,587 А; I5 = 0,405 А.
5. Для цепи постоянного тока (см. рисунок) заданы величины сопротивлений резисторов, ЭДС и внутреннего сопротивления источника (см. таблицу). Определить величину тока I в ветви с источником.
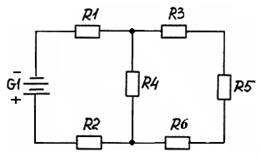
Таблица - Исходные данные к задаче №5
| № п/п | R1, Ом | R2, Ом | R3, Ом | R4, Ом | R5, Ом | R6, Ом | EG1, B | RG1, Ом |
6. Для цепи постоянного тока (см. рисунок) заданы величины сопротивлений резисторов, ЭДС и внутреннего сопротивления источников (см. таблицу). Определить токи во всех ветвях.
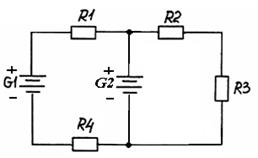
Таблица - Исходные данные к задаче №6
| № п/п | R1, Ом | R2, Ом | R3, Ом | R4, Ом | EG1, B | RG1, Ом | EG2, B | RG2, Ом |
Расчет цепи методом узлового напряжения
Задача 1. В схеме рис. 1.31 E1 = 60 В, E2 = 48 В, E3 = 6 В, R1 = 200 Ом, R2 = 100 Ом, r03 = 0,5 Ом, R3 = 9,5 Ом. Определить токи в ветвях схемы.
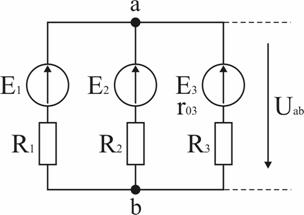
Анализ и решение задачи 1
1. Вычисление узлового напряжения. Для схемы с двумя узлами напряжение между ними можно подсчитать по формуле
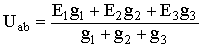 ,
,
где Еi – ЭДС i-й ветви, gi – ее проводимость 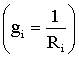 .
.
Подставляем числовые значения:
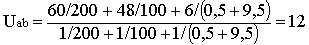 В.
В.
2. Расчет токов в ветвях
Токи определяем на основании закона Ома для ветви с источником: напряжение на зажимах источника равно его ЭДС минус падение напряжения на его внутреннем сопротивлении:
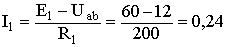 А;
А;
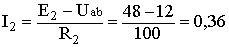 А;
А;
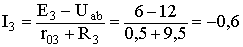 А.
А.
7.Для цепи, принципиальная электрическая схема которой изображена на рисунке, заданы величины сопротивлений резисторов, ЭДС и внутреннего сопротивления источников (см. таблицу). Определить токи во всех ветвях.
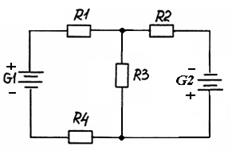
Таблица - Исходные данные к задаче №7
| № п/п | R1, Ом | R2, Ом | R3, Ом | R4, Ом | EG1, B | RG1, Ом | EG2, B | RG2, Ом |
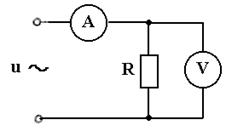
8. К источнику синусоидального напряжения промышленной частоты подключен резистор с сопротивлением R = 20 Ом (см. рисунок). Показания вольтметра равны 220 В. Определить показания амперметра и функцию мгновенного тока в цепи.
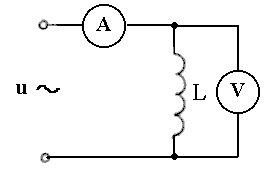
9. К источнику синусоидального напряжения промышленной частоты подключена катушка, сопротивление проводов которой RL = 2 Ом, а индуктивность L = 0,4 Гн (см. рисунок). Показания амперметра равны 1 А. Определить показания вольтметра и функцию мгновенного напряжения в цепи.
10. Цепь подключена к источнику синусоидального напряжения (см. рисунок). Сопротивление резистора R1= 20 Ом. Сопротивление проводов катушки RL = 2 Ом. Индуктивность катушки L = 0,5 Гн. Емкость конденсатора С = 100 мкФ. Общее напряжение цепи определяется выражением 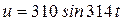 . Определить показания вольтметра и режим работы цепи.
. Определить показания вольтметра и режим работы цепи.
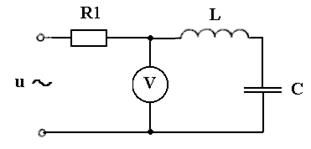
11. Цепь подключенакисточнику синусоидального напряжения промышленной частоты (см. рисунок). Действующее напряжение источника 220 В. Для своего варианта параметров, соответствующего номеру по журналу учебной группы (см. таблицу), определить показания измерительных приборов.
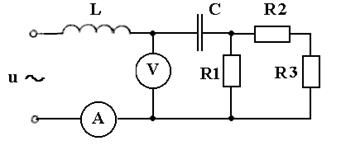
Таблица - Исходные данные к задаче №11
| № п/п | С, мкФ | L, мГн | R1, Ом | R2, Ом | R3, Ом |
12. Цепь подключенакисточнику синусоидального напряжения промышленной частоты (см. рисунок). Заданы показания вольтметра и параметры элементов цепи (см. таблицу). Определить показания амперметра.
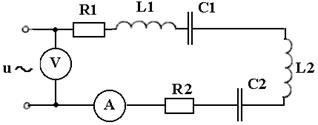
Рис. - Принципиальная электрическая схема цепи
Таблица - Исходные данные к задаче №12
| № , п/п | С1, мкФ | L1 мГн | С2, мкФ | L2, мГн | R1, Ом | R2, Ом | U, B |
13. Цепь подключенакисточнику синусоидального напряжения промышленной частоты (см. рисунок). Действующее напряжение источника 220 В. Заданы параметры элементов цепи (см. таблицу). Определить показания измерительных приборов.
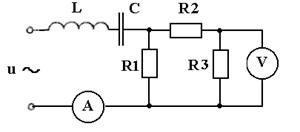
Таблица - Исходные данные к задаче №13
| № п/п | С, мкФ | L, мГн | R1, Ом | R2, Ом | R3, Ом |
14. К источнику синусоидального напряжения промышленной частоты с действующим значением U = 220 В подключена цепь, образованная последовательным соединением резистора, катушки индуктивности и конденсатора (см. рисунок). Сопротивление резистора R1= 20 Ом. Сопротивление проводов катушки RL = 2 Ом. Индуктивность катушки L = 0,5 Гн. Емкость конденсатора С = 100 мкФ. Определить показания вольтметра.
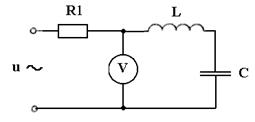
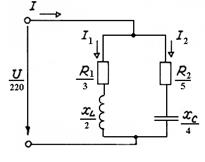
15. К источнику синусоидального напряжения подключена цепь, схема замещения которой показана на рисунке. Определить токи во всех ветвях, если R1= 3 Ом, R2 = 5 Ом, XL = 2 Ом, XС = 4 Ом, U=220 B.
16. Цепь подключенакисточнику синусоидального напряжения промышленной частоты (см. рисунок). Амперметр показывает ток 1 А. Заданы параметры элементов цепи (см. таблицу). Определить показания вольтметров. Сделать проверку методом векторных диаграмм.
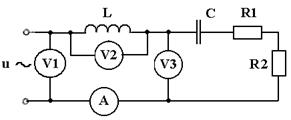
Таблица - Исходные данные к задаче №16
| № п/п | С, мкФ | L, мГн | RL, Ом | R1, Ом | R2, Ом |
17. Цепь подключенакисточнику синусоидального напряжения промышленной частоты (см. рисунок). Показания вольтметра - 220 В. Параметры элементов цепи указаны в таблице. Определить показания амперметров. Сделать проверку методом векторных диаграмм.
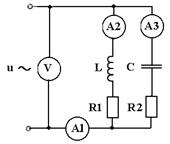
Таблица - Исходные данные к задаче №17
| № п/п | С, мкФ | L, мГн | R1, Ом | R2, Ом |
Задача 1. Электрическая цепь, показанная на рис. 6.8, питается от источника синусоидального тока с частотой 200 Гц и напряжением 120 В. Дано: R = 4 Ом, L = 6,37 мГн, C = 159 мкФ.
Вычислить ток в цепи, напряжения на всех участках, активную, реактивную, и полную мощности. Построить векторную диаграмму, треугольники сопротивлений и мощностей.
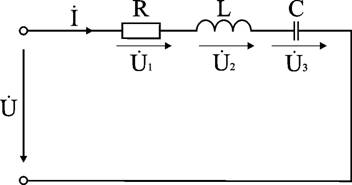
Анализ и решение задачи 1
1. Вычисление сопротивлений участков и всей цепи
Индуктивное реактивное сопротивление
XL = 2πf L = 2×3,14×200×6,37·10-3 Ом.
Емкостное реактивное сопротивление
XC = 1 / (2πf C) = 1 / (2×3,14×200×159·10-6) Ом.
Реактивное и полное сопротивления всей цепи:
X = XL - XC = 3 Ом; 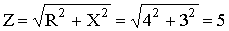 Ом.
Ом.
2. Вычисление тока и напряжений на участках цепи
Ток в цепи
I = U / Z = 120 / 5 А.
Напряжения на участках:
U1 = R I = 96 В; U2 = XL I = 192 В; U3 = XC I = 120 В.
3. Вычисление мощностей
Активная мощность
P = R I2 = U1 I = 2304 Вт.
Реактивные мощности:
QL = XL I2 = U2 I = 4608 ВАр; QC = XC I2 = U3 I = 2880 ВАр.
Полная мощность цепи
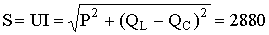 ВА.
ВА.
4. Расчет цепи методом комплексных чисел
Запишем в комплексном виде сопротивление каждого элемента и всей цепи
R = 4ej0° = 4 Ом; XL = 8e+j90° = j8 Ом; XC = 5e-j90° = -j5 Ом.
Z = R + j(XL - XC) = 4 + j(8 - 5) Ом.
На комплексной плоскости в масштабе: в 1 см – 2 Ом, построим треугольник сопротивлений (рис. 6.9. а).
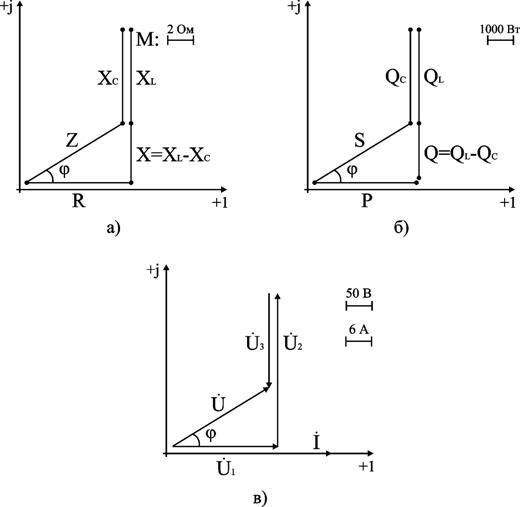
Из треугольника определим величину полного сопротивления Z и угол фазового сдвига φ
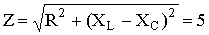 Ом;
Ом;
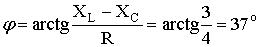 .
.
В показательной форме полное сопротивление всей цепи запишется в виде
Z = Ze+jφ = 5e+j37°Ом.
Примем начальную фазу приложенного к цепи напряжения за нуль и определим по закону Ома ток в данной цепи
Í = Ú / Z = 120e+j0° / 5e+j37° А.
Следовательно, в данной цепи ток отстает по фазе от напряжения на угол φ. Зная величину тока I, определим мощности для отдельных элементов и всей цепи.
P = 2304 Вт; QL = 4608 ВАр; QC = 2880 ВАр.
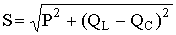 .
.
Треугольник мощностей в масштабе: в 1 см – 1000 Вт (ВАр); (ВА), построим (рис. 6.9. б) на основе выражения для полной мощности
S2 = P2 + (QL - QC)2.
Для построения векторных диаграмм по току и напряжениям примем начальную фазу тока равной нулю, т.к. ток I в данной схеме является одним и тем же для всех элементов в цепи.
Í = Ie+j0° / 24e+j0°А.
Запишем выражения для напряжений в комплексной форме
Ú1 = R Í = 96e+j0° В; Ú2 = XL Í = 192e+j90°В;
Ú3 = XC Í = 120e-j90° В; Ú = Z Í = 120e+j37° В.
Выберем масштабы для векторной диаграммы: в 1 см – 6 А; в 1 см – 50 В. Векторная диаграмма напряжений строится на основе второго закона Кирхгофа для данной цепи
Ú = Ú1 + Ú2 + Ú3.
Векторная диаграмма цепи показана на рис. 6.9. в. При последовательном соединении элементов построение диаграммы начинают с вектора тока Í, по отношению к которому ориентируются вектора напряжений на участках цепи: напряжение на активном сопротивлении Ú1 совпадает с ним по направлению, напряжение на индуктивности Ú2 опережает его на 90°, на емкости отстает на 90°. Полное напряжение Ú строится как их векторная сумма.
18. Составить уравнения баланса токов и напряжений для цепи, изображенной на рисунке
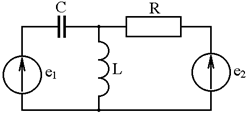
Независимой проверкой является уравнение баланса мощностей: сумма мощностей источников равна сумме мощностей, расходуемых в резистивных элементах схемы. Т.к. элемент схемы с ЭДС может работать как в режиме источника, так и в режиме потребителя, соответствующее слагаемое в левой части уравнения берется с плюсом, если Е и I совпадают по направлению (источник), и с минусом, если направления противоположны (потребитель).
Мощности элементов схемы с ЭДС:
E1I1+ E2I2 - E3I3 = 60 * 1 * 1,093 + 80 * 0,911 - 70 * 0,506 = 104,04 Вт.
Мощности, расходуемые в резистивных элементах схемы:
I12R1 + I22R2 + I32r03 + I42R4+ I52R5 = 1,0932 * 20 + 0,9112 * 50 + 0,5062 * 5 + 0,5872 * 65 + 0,4052 * 85 = 103,01 Вт
SEI = SP Баланс мощностей сошелся, следовательно задача решена верно.
19. Составить уравнения баланса токов и напряжений для цепи, изображенной на рисунке
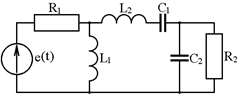
20. Составить уравнения по методу контурных токов, записать выражения для собственных и взаимных сопротивлений цепи
https://www.youtube.com/watch?v=42OUspeT0Zc
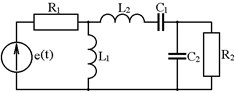
21. Составить уравнения по методу узловых напряжений, записать выражения для собственных и взаимных проводимостей цепи
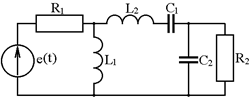
22. Последовательный колебательный контур имеет следующие параметры: 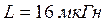 ,
, 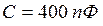 ,
, 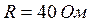 . Определить резонансную частоту
. Определить резонансную частоту 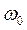 , характеристическое сопротивление
, характеристическое сопротивление 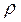 , добротность
, добротность 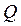 , затухание
, затухание 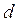 , полосу пропускания
, полосу пропускания 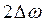 , сопротивление контура на резонансной частоте.
, сопротивление контура на резонансной частоте.
Резонанс токов возможен в цепи, содержащей параллельно соединенные индуктивности и емкости (Рис. 9)
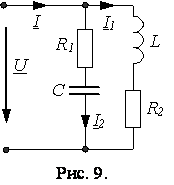
http://edu.tltsu.ru/er/book_view.php?book_id=2fc&page_id=3457
Условие резонанса токов:

Угловая резонансная частота:
 ,
,
где характеристическое сопротивление
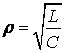 ;
;
добротность контура
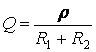 ;
;
сопротивление контура при резонансе токов
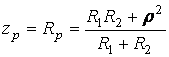 ;
;
ток неразветвленной части цепи при резонансе
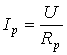 ;
;
полоса пропускания определяется из условия, что ток на частотах f1 и f2, соответствующих границы полосы пропускания, уменьшается в 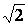 ;
;
абсолютное значение полосы пропускания:
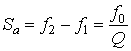 ;
;
относительное значение полосы пропускания:
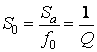 .
.
Пример 2.3.1
Электрическая цепь состоит из последовательно соединенных активного сопротивления 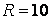 Ом, катушки индуктивностью
Ом, катушки индуктивностью 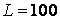 мкГн и конденсатора емкостью
мкГн и конденсатора емкостью 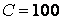 пФ.
пФ.
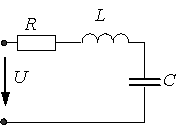
Определить резонансную частоту 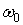 , характеристическое сопротивление ρ, затухание и добротность контура. Чему равны ток, расходуемая в цепи мощность, напряжение на индуктивности и емкости, если контур включен на напряжении 1 В? Вычислить абсолютное значение полос пропускания контура.
, характеристическое сопротивление ρ, затухание и добротность контура. Чему равны ток, расходуемая в цепи мощность, напряжение на индуктивности и емкости, если контур включен на напряжении 1 В? Вычислить абсолютное значение полос пропускания контура.
Решение:
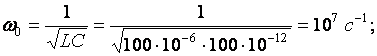
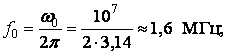
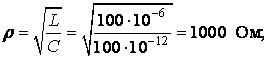
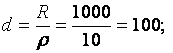
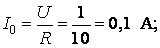
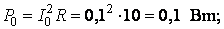
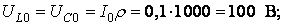
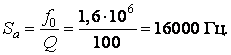
Пример 2.3.2
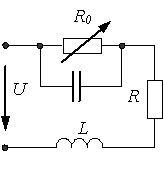
На зажимах цепи поддерживается постоянное по действующему значению напряжение 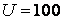 В,
В, 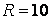 Ом,
Ом, 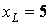 Ом,
Ом, 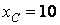 Ом.
Ом.
Определить 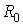 , при котором цепь будет находиться в резонансе.
, при котором цепь будет находиться в резонансе.
Решение:
Условие резонанса напряжений
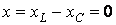 ,
,

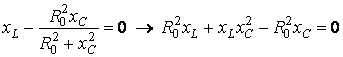 ;
;
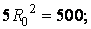
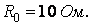
Ток при резонансе
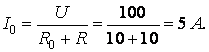
23. Параллельный колебательный контур имеет следующие параметры: 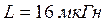 ,
, 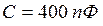 ,
, 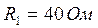 ,
, 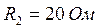 . Определить резонансную частоту
. Определить резонансную частоту 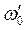 , характеристическое сопротивление
, характеристическое сопротивление 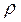 , добротность
, добротность 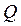 , затухание
, затухание 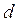 , полосу пропускания
, полосу пропускания 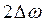 , сопротивление контура на резонансной частоте.
, сопротивление контура на резонансной частоте.
24. К последовательному колебательному контуру с параметрами L=2 мГн; С=1,5 нФ; R=32 Ом подключен источник гармонической ЭДС. Определить: абсолютную, относительную и обобщённую расстройки на частоте 100кГц, найти модуль и аргумент входного комплексного сопротивления контура на этой частоте.
25. К последовательному колебательному контуру с параметрами L=0,5 мГн; С=2,5 нФ; R=52 Ом подключен источник гармонической ЭДС. Определить: абсолютную, относительную и обобщённую расстройки на частоте 92кГц, найти модуль и аргумент входного комплексного сопротивления контура на этой частоте.
26. К последовательному колебательному контуру с параметрами L=2,5 мГн; С=3,5 нФ; R=62 Ом подключен источник гармонической ЭДС. Определить: абсолютную, относительную и обобщённую расстройки на частоте 88кГц, найти модуль и аргумент входного комплексного сопротивления контура на этой частоте.
27. Определить напряжение на катушке с активным сопротивлением R=3 Ом, и индуктивным XL=4 Ом, если ток в ней 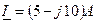 . Определить полную, активную и реактивную мощности катушки.
. Определить полную, активную и реактивную мощности катушки.
28. Определить напряжение на катушке с активным сопротивлением R=4 Ом, и индуктивным XL=40 Ом, если ток в ней 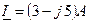 . Определить полную, активную и реактивную мощности катушки.
. Определить полную, активную и реактивную мощности катушки.
29. Коэффициент А-формы несимметричного четырёхполюсника А = 2 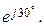 Укажите, чему равно отношение U2/U1 ЧП в режиме ХХ?
Укажите, чему равно отношение U2/U1 ЧП в режиме ХХ?
 2
2 
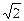
 1
1  0,5
0,5  0
0
30. Укажите соотношения входного и выходного сопротивлений ЧП в режиме согласования с нагрузкой и несогласования с источником?
 Z2н = Z2с
Z2н = Z2с  Z2н ¹ Z2с
Z2н ¹ Z2с  Z2н = Z2с
Z2н = Z2с  Z2н ¹ Z2с
Z2н ¹ Z2с
Z1с¹ Zи Zи ¹ Z1с Zи = Z1с Zи = Z1с
31. Укажите, чему равно отношение напряжений U2/U1 в режиме ХХ для Т-образного ЧП, в продольные ветви которого включены индуктивные элементы L, а в поперечную - ёмкостный элемент С?

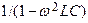

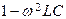

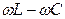
 1
1 
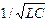
32. Укажите, чему равно характеристическое сопротивление Z1с ЧП, если известны результаты опытов ХХ и КЗ: Z1Х = 5 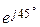 Ом; Z1К = 5
Ом; Z1К = 5 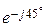 Ом; Z2Х = 2
Ом; Z2Х = 2 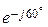 Ом?
Ом?
 5
5 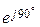
 5
5 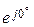
 5
5 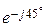
 2
2 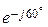
 0
0
33. Укажите, чему равен коэффициент С А-формы симметричного Т-образного ЧП, в продольные ветви которого включены сопротивления, равные 3 + j4 Ом, а в поперечную ветвь - элемент, сопротивление которого равно j5 Ом?
 0,2
0,2 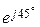 См
См  0,2 См
0,2 См  j0,2 См
j0,2 См  -j См
-j См  -j0,2 См.
-j0,2 См.
34. Укажите выражение собственной постоянной ослабления (в дБ) симметричного ЧП при его согласованном включении.

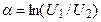

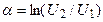

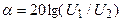

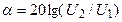
35. Укажите, можно ли по найденным из опытов ХХ и КЗ входным сопротивлениям пассивного ЧП определить параметры Т- и П-образной схем замещения ЧП?
 Да
Да  Нет
Нет
36. Укажите размерность коэффициента D в А-форме записи уравнений ЧП.
 Ом
Ом  Безразмерный
Безразмерный  См
См  Ом/с
Ом/с
37. Укажите, какие коэффициенты А-формы записи уравнений несимметричного ЧП можно рассчитать при коротком замыкании на выходе ЧП при известных параметрах элементов и схеме их соединения?
 Только А
Только А  С и D
С и D  А и D
А и D  B и С
B и С  B и D
B и D
38. Укажите, выражение А×D – B×C = 1 есть уравнение связи коэффициентов несимметричного пассивного ЧП?
 Да
Да  Нет
Нет
39. Изобразите АЧХ фильтра нижних частот и АЧХ фильтра верхних частот на них покажите полосы пропускания, полосы затухания и частоты среза.
40. Изобразите АЧХ полосового пропускающего фильтра и на ней покажите полосу пропускания, полосу затухания и частоты среза.
41. Изобразите АЧХ полосового заграждающего фильтра и на ней покажите полосу пропускания, полосу затухания и частоты среза.
42. Определите вид звена электрического фильтра, схема которого приведена на рисунке
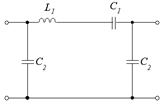
43. Изобразить примерный вид АЧХ фильтра, представленного на рисунке и определить его назначение.
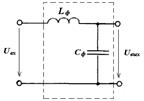
44. Изобразить примерный вид АЧХ фильтра, представленного на рисунке и определить его назначение.
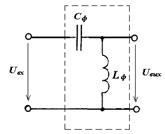
45. Изобразить примерный вид АЧХ фильтра, представленного на рисунке и определить его назначение.
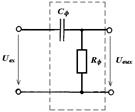
46. Качественно изобразить функцию переходного тока в цепи после коммутации, определить постоянную времени и время переходного процесса в цепи, параметры и схема замещения которой показаны на рисунке.
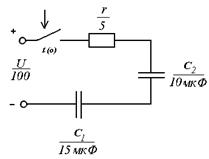
47. Качественно изобразить функцию переходного тока в цепи после коммутации, определить постоянную времени и время переходного процесса в цепи, параметры и схема замещения которой показаны на рисунке.
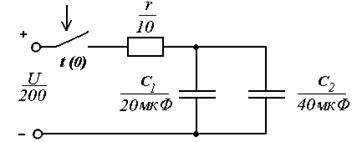
48. Качественно изобразить функцию переходного тока в цепи после коммутации, определить постоянную времени и время переходного процесса в цепи, параметры и схема замещения которой показаны на рисунке.
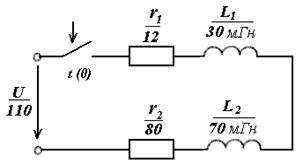
49. Постройте операторную схему замещения и, используя законы Кирхгофа в операторной форме, составьте уравнение электрического равновесия, схема замещения которой приведена на рисунке.
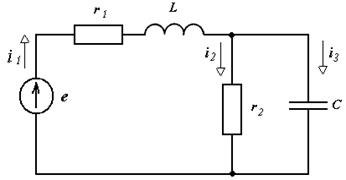
50. Постройте операторную схему замещения и, используя законы Кирхгофа в операторной форме, составьте уравнение электрического равновесия, схема замещения которой приведена на рисунке.
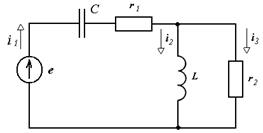
51. Каков порядок составления математической модели (уравнений состояния) нелинейной цепи?
52. Каков алгоритм моделирования нелинейной цепи в пакете прикладных программMATHCAD?
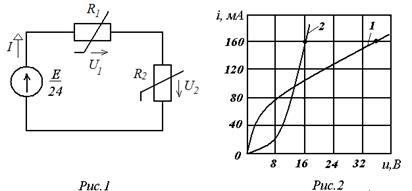
53. Найдите дифференциальные сопротивления нелинейных резисторов R1 и R2 (рис.1), ВАХ которых приведены на рис. 2 (кривые 1 и 2). Рабочая точка для R1 при U1 = 8 B и I1 = 80mA; рабочая точка для R2 при U2 = 12 B и I2 = 80mA.
54. ВАХ нелинейного резистивного элемента описывается выражением i = au2. Покажите, что гармоническое напряжение u = Um cos ωt, приложенное к элементу, вызывает в нем негармонический ток.
55. Первичные параметры однородной воздушной линии связи имеют значения: r0 = 90 Ом/км L0 = 2,22 · 10-3 Гн/км; g0 = 0,0557 · 10-3 См/км; С0 = 0,1 · 10-6 Ф/км. Определить волновое сопротивление линии (Zв= ?)
56. В однородной линии связи при частоте f = 1 КГц комплексное продольное сопротивление на единицу длины линии Z0 = 100 e j82º, Ом/км, а поперечная комплексная проводимость Y0 = 0,4 · 10-3 е j82º Cм/км. Определить комплексный коэффициент распространения волны (γ = ?), коэффициент затухания (α =?) и коэффициент фазы (β =?).
Рассмотрены на заседании кафедры,
протокол № ___ от _____________ .
Доцент кафедры «Радиоэлектроника»
к.т.н. доцент Н.В.Руденко
