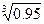Застосування диференціала до наближених обчислень
ГЕОМЕТРИЧНИЙ ТА МЕХАНІЧНИЙ ЗМІСТ ПОХІДНОЇ.ДОТИЧНА ДО КРИВОЇ.
Механічний зміст похідної: похідна S`(t) є величиною миттєвої швидкості в момент t тіла, що рухається за законом S=S(t)/
Геометричний зміст похідної:похідна f`(x) дорівнює кутовому коефіцієнту дотичної до графіка функції у=f(x) в точці з абсцисою х.
Рівняння дотичної до графіка функції у=f(x) у точці з абсцисою 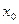 має вигляд
має вигляд
У= 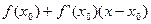
ЗАВДАННЯ САМОСТІЙНОЇ РОБОТИ
1.В якій точці дотична до графіка функції у= 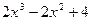 паралельна осі абсцис.
паралельна осі абсцис.
2.При якому значенні а крива у= 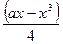 перетинає вісь Ох під кутом
перетинає вісь Ох під кутом 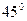 .
.
3.Скласти рівняння дотичної до параболи у= 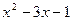 в точці (3;4).
в точці (3;4).
4.Два тіла рухаються прямолінійно : одне згідно закону 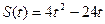 ,а друге – згідно закону
,а друге – згідно закону 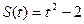 .Знайти момент часу, коли швидкості цих тіл будуть рівними.
.Знайти момент часу, коли швидкості цих тіл будуть рівними.
ЗВ'ЯЗОК МІЖ НЕПЕРЕРВНІСТЮ ТА ДИФЕРЕНЦІЙОВНІСТЮ ФУНКЦІЙ .
ТЕОРЕМА. Якщо функція у=f(х) диференційовна в деякій точці 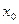 , то вона в цій точці
, то вона в цій точці
неперервна.
НАСЛІДОК.З цієї теореми випливає , що неперервність функції є необхідною умовою
Диференційовності функції . Це означає, що в точках розриву функція не
має похідних , тобто вона не диференційовна.
ОСНОВНІ ТЕОРЕМИ ДИФЕРЕНЦІАЛЬНОГО ЧИСЛЕННЯ . ПРАВИЛО ЛОПІТАЛЯ.
Теорема Лагранжа. Якщо функція у=f(x) неперервна на [a,b] і має похідну в усіх точках
інтервала (а;b) , то всередині цього інтервалу існує хоч би одна точка с
( а <c<b) така ,що виконується рівність
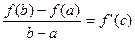 .
.
Теорема Ролля. Якщо функція у=f(x) неперервна на відрізку [a;b] ,диференційовна в усіх
внутрішніх точках цього відрізка ,а на його кінцях приймає рівні значен-
ня .то похідна f`(x) дорівнює нулю хоч би в одній внутрішній точці с
(a<c<b) цього відрізка.
Правило Лопіталя. Нехай f(x) та g(x)-неперервні та мають похідні в усіх х 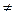 а з околу точ-
а з околу точ-
ки х=а ,а в точці а рівні нулю або нескінченності.Тоді границя відно-
шення функцій дорівнює границі відношення їх похідних ,якщо остання
існує, тобто
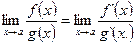 .
.
Якщо відношення 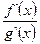 знову є невизначеністю вигляду
знову є невизначеністю вигляду 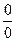 або
або 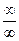 і похідні f`(x) та
і похідні f`(x) та
g`(x) задовільняють умовам правила Лопіталя , то для обчислення границі можна засто-совувати правило Лопіталя вдруге і т. д.
Приклад. Обчислити 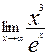 .
.
В данному випадку 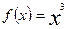 та
та 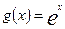 задовольняють умовам правила Лопіталя .Відно-
задовольняють умовам правила Лопіталя .Відно-
шення їх є невизначеністю вигляду 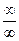 при х
при х 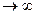 . Застосувавши правило Лопіталя,
. Застосувавши правило Лопіталя,
одержуємо:
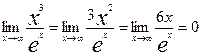 .
.
ЗАВДАННЯ САМОСТІЙНОЇ РОБОТИ.
Обчислити границі:
1. 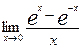
2. 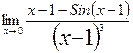
3. 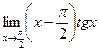
4. 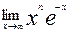
Застосування диференціала до наближених обчислень

Головна частина приросту функції , яка лінійно залежить від приросту аргумента,називається диференціалом функції , позначається dy і обчислюється згідно
формули dy=f`( 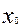 )
) 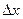 .
.
Диференціал використовується для обчислення наближеного значення приросту функції
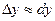 та наближеного значення фукції f(x+
та наближеного значення фукції f(x+ 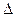 x)
x) 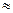 f(x)+dу.
f(x)+dу.
Приклад. Користуючись поняттям диференціала функції , знайти наближене значення
приросту функції f(x)= 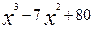 при зміні аргумента х від 5 до 5,01.
при зміні аргумента х від 5 до 5,01.
Розв’язування. 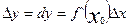 , f`(x)=
, f`(x)= 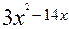 , f`( 5)=
, f`( 5)= 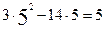 ,
, 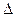 х=5,01-5=0,01
х=5,01-5=0,01
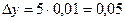 .
.
Приклад.Знайти наближене значення функції у= 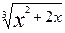
 при х=2,004.
при х=2,004.
Розв’язування. f(x+ 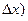 =f(2,004)=f(2+0,004)
=f(2,004)=f(2+0,004) 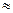 f(2)+dу
f(2)+dу 
f(2)= 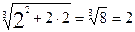
 , f`(x)=
, f`(x)= 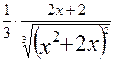 , f`(2)=
, f`(2)= 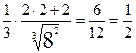
dу= 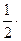 0,004=0,002 f(2,004)=2+0,002=2,002.
0,004=0,002 f(2,004)=2+0,002=2,002.
Література. В.Т.Лисичкин , И.Л.Соловейчик. Математика.
В.В.Барковський , Н.В.Барковська . Математика для економістів.
ІНДИВІДУАЛЬНІ СЕМЕСТРОВІ ЗАВДАННЯ
Знайти наближене значення приросту функції при заданій зміні аргументу
1. у= 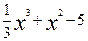 від 3 до 3.1
від 3 до 3.1
2. у= 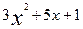 при х=3 і
при х=3 і 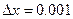
3.у= ln x при х=10 і 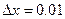
4.у= 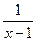 при х=2 і
при х=2 і 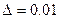
5. у= 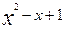 при х=3 і
при х=3 і 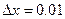
6. у= 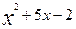 при х=1 і
при х=1 і 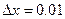
7. у= 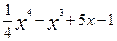 від 1 до 1.02
від 1 до 1.02
8. у= 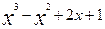 при х=2 і
при х=2 і 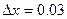
9. у= 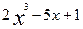 при х=3 і
при х=3 і 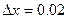
10. у= 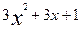 при х=2 і
при х=2 і 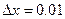
Обчислити значення функцій
11. у= 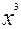 при х=10.03
при х=10.03
12. у= 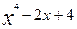 при х=3.002
при х=3.002
13. у= 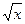 при х=24.99
при х=24.99
14. у= 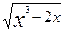 при х= 1.96
при х= 1.96
15. 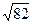
16. 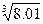 24.
24. 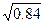
17. 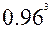 25.
25. 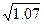
18. 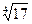 26.
26. 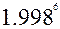
19. 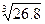 27.
27. 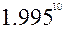
20. 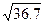 28.
28. 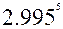
21. 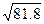 29.
29. 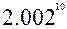
22. 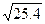 30.
30. 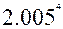
23.