Матрица ұғымы және түрлері

Анықтама. Сандардан немесе қандай да бір басқа элементтерден тұратын тікбұрышты кестені матрица деп атайды да, оны екі жағынан жақша немесе қос түзу сызықтармен шектеп жазады.

Мысалға, матрицалар төмендегідей:

, ,

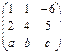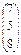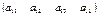
түрлерінде жазылады.

Анықтауыштардағы сияқты матрицалар да жатық жолдардан және тік бағаналардан тұрады. Сондықтан да матрицаның элементтерінің орындарын жатық жол және тік бағана нөмірлері арқылы ажырататын боламыз. Ал матрицаның анықтауыштан айырмашылығы – анықтауыш сияқты бір санға тең болмайтындығында.

Матрицаның қысқаша бір ғана әріппен 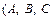т.с.с.) белгілеп жазуға болады, әрине бір әріппен жазылған матрицаны кестие деп түсінуіміз керек.

Егер матрицаның элементтерін 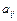арқылы белгілейтін болсақ, онда жалпы түрде 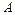матрицасы деп мына

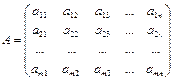
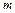жатық жолдан және 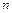тік бағанадан тұратын тікбұрышты кестені ұғамыз.

Анықтауыш сияқты матрицаның элементтерін де екі индекс арқылы жазған қолайлы. Оның біріншісі – жатық жол нөмірін, ал екіншісі – тік бағана нөмірін көрсететін болады. Матрицада жалпы мөлшер ұғымын ғана пайдалануға болады. Тек 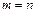болған жағдайда ғана матрица реті айтылады.

Егер матрицаның мөлшері 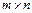, яғни 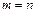болса, она ондай матрицаны квадрат матрица деп атайды.

Матрицаның жатық жолдары мен тік бағаналарының орындарын ауыстыруға болады. Осындай әрекет нәтижесінде шыққан матрицаны транспозицияланған матрица деп атайды да, оны 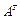түрінде белгілейді.

Мысалы, берілген матрица

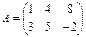
болса, онда транспозицияланған матрица

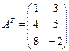
болады.

Егер берілген матрица 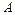өзінің транспозицияланған матрицасымен дәл келетін болса, яғни

,

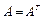Онда мұндай матрица симметриялы матрица деп аталады. Матрицаның бұл шартын

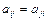
түрінде жазуға болады.

Матрицалардың барлық түрлерінің ішінде тек квадрат матрианың ғана анықтауышы болады және оны 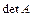не , не 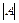түрінде жазады. Егер 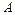квадрат матриа болса, онда

,

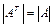Демек анықтауыштың шамасы оны транспозициялаудан өзгермейді.