Множественная регрессия и корреляция

Решение Тестовых заданий

Парная регрессия и корреляция

1. Наиболее наглядным видом выбора уравнения парной регрессии является:

а) аналитический;

б) графический;

в) экспериментальный (табличный).

Ответ: б) графический.

В парной регрессии выбор вида математической функции 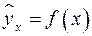может быть осуществлен тремя методами:

1) графическим;

2) аналитическим, т.е. исходя из теории изучаемой взаимосвязи;

3) экспериментальным.

При изучении зависимости между двумя признаками графический метод подбора вида уравнения регрессии достаточно нагляден. Он основан на поле корреляции.

2. Рассчитывать параметры парной линейной регрессии можно, если у нас есть:

а) не менее 5 наблюдений;

б) не менее 7 наблюдений;

в) не менее 10 наблюдений.

Отчет: б) не менее 7 наблюдений

Считается, что число наблюдений должно в 7-8 раз превышать число рассчитываемых параметров при переменной 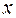. Это означает, что искать линейную регрессию, имея менее 7 наблюдений, вообще не имеет смысла. Если вид функции усложняется, то требуется увеличение объема наблюдений, ибо каждый параметр при 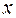должен рассчитываться хотя бы по 7 наблюдениям.

3. Суть метода наименьших квадратов состоит в:

а) минимизации суммы остаточных величин;

б) минимизации дисперсии результативного признака;

в) минимизации суммы квадратов остаточных величин.

Ответ: б) минимизации дисперсии результативного признака

Классический подход к оцениванию параметров линейной модели множественной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака 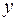от расчетных 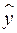минимальна:

.

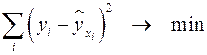4. Коэффициент линейного парного уравнения регрессии:

а) показывает среднее изменение результата с изменением фактора на одну единицу;

б) оценивает статистическую значимость уравнения регрессии;

в) показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%.

Ответ: а) показывает среднее изменение результата с изменением фактора на одну единицу

Параметр 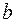называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу.

Возможность четкой экономической интерпретации коэффициента регрессии сделала линейное уравнение регрессии достаточно распространенным в эконометрических исследованиях.

На основании наблюдений за 50 семьями построено уравнение регрессии , где – потребление, – доход. Соответствуют ли знаки и значения коэффициентов регрессии теоретическим представлениям?

а) да;

б) нет;

в) ничего определенного сказать нельзя.

Ответ: а) да (пример рассматривали на паре с доходами и расходами)

6. Суть коэффициента детерминации 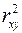состоит в следующем:

а) оценивает качество модели из относительных отклонений по каждому наблюдению;

б) характеризует долю дисперсии результативного признака 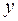, объясняемую регрессией, в общей дисперсии результативного признака;

в) характеризует долю дисперсии 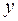, вызванную влиянием не учтенных в модели факторов.

Ответ: б) характеризует долю дисперсии результативного признака у, объясняемую регрессией, в общей дисперсии результативного признака

Квадрат индекса корреляции носит название индекса детерминации и характеризует долю дисперсии результативного признака 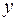, объясняемую регрессией, в общей дисперсии результативного признака:

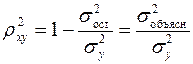, (1.22)

т.е. имеет тот же смысл, что и в линейной регрессии; .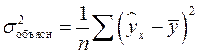

7. Качество модели из относительных отклонений по каждому наблюдению оценивает:

а) коэффициент детерминации ;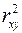

б) 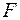-критерий Фишера;

в) средняя ошибка аппроксимации .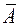

Ответ: а) коэффициент детерминации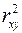

Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции 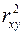, называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака 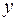, объясняемую регрессией, в общей дисперсии результативного признака:

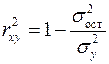, (1.7)

где , .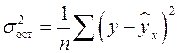

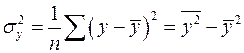8. Значимость уравнения регрессии в целом оценивает:

а) 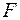-критерий Фишера;

б) 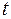-критерий Стьюдента;

в) коэффициент детерминации .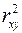

Ответ: а) F-критерий Фишера

Оценка значимости уравнения регрессии в целом производится на основе 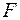-критерия Фишера, которому предшествует дисперсионный анализ. В математической статистике дисперсионный анализ рассматривается как самостоятельный инструмент статистического анализа.

9. Классический метод к оцениванию параметров регрессии основан на:

а) методе наименьших квадратов:

б) методе максимального правдоподобия:

в) шаговом регрессионном анализе.

Ответ: в) шаговом регрессионном анализе

Отбор факторов, включаемых в регрессию, является одним из важнейших этапов практического использования методов регрессии. Подходы к отбору факторов на основе показателей корреляции могут быть разные. Они приводят построение уравнения множественной регрессии соответственно к разным методикам. В зависимости от того, какая методика построения уравнения регрессии принята, меняется алгоритм ее решения на ЭВМ.

Наиболее широкое применение получили следующие методы построения уравнения множественной регрессии:

1. Метод исключения – отсев факторов из полного его набора.

2. Метод включения – дополнительное введение фактора.

3. Шаговый регрессионный анализ – исключение ранее введенного фактора.

При отборе факторов также рекомендуется пользоваться следующим правилом: число включаемых факторов обычно в 6–7 раз меньше объема совокупности, по которой строится регрессия. Если это соотношение нарушено, то число степеней свободы остаточной дисперсии очень мало. Это приводит к тому, что параметры уравнения регрессии оказываются статистически незначимыми, а 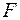-критерий меньше табличного значения.

10. Остаточная сумма квадратов равна нулю:

а) когда правильно подобрана регрессионная модель;

б) когда между признаками существует точная функциональная связь;

в) никогда.

Ответ: в) никогда

Согласно основной идее дисперсионного анализа, общая сумма квадратов отклонений переменной 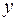от среднего значения 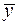раскладывается на две части – «объясненную» и «необъясненную»:

,

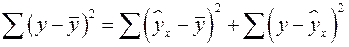где 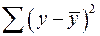– общая сумма квадратов отклонений; 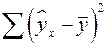– сумма квадратов отклонений, объясненная регрессией (или факторная сумма квадратов отклонений); 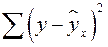– остаточная сумма квадратов отклонений, характеризующая влияние неучтенных в модели факторов.

11. Объясненная (факторная) сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:

а) ;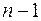

б) ;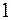

в) .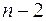

Ответ: б)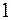

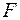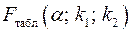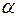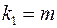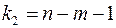Фактическое значение -критерия Фишера (1.9) сравнивается с табличным значением при уровне значимости и степенях свободы и . При этом, если фактическое значение 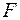-критерия больше табличного, то признается статистическая значимость уравнения в целом.

Для парной линейной регрессии 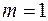, поэтому

.

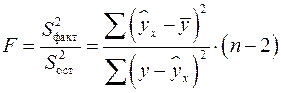12. Остаточная сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:

а) ;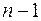

б) ;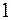

в) .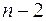

Ответ: в) .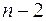

Величина стандартной ошибки совместно с 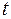-распределением Стьюдента при 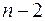степенях свободы применяется для проверки существенности коэффициента регрессии и для расчета его доверительного интервала.

Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т.е. определяется фактическое значение 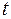-критерия Стьюдента: 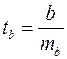которое затем сравнивается с табличным значением при определенном уровне значимости 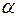и числе степеней свободы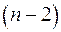

13. Общая сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:

а) ;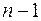

б) ;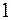

в) .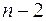

Ответ: а)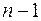

Общая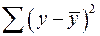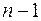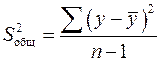

14. Для оценки значимости коэффициентов регрессии рассчитывают:

а) 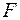-критерий Фишера;

б) 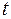-критерий Стьюдента;

в) коэффициент детерминации .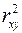

Ответ: в) коэффициент детерминации .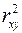

Индекс детерминации 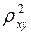можно сравнивать с коэффициентом детерминации 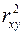для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем величина 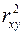меньше 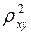. А близость этих показателей указывает на то, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию. Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции 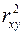, называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака 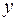, объясняемую регрессией, в общей дисперсии результативного признака:

,

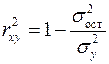где , .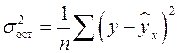

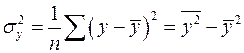Соответственно величина 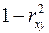характеризует долю дисперсии 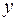, вызванную влиянием остальных, не учтенных в модели, факторов.

15. Какое уравнение регрессии нельзя свести к линейному виду:

а) ;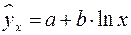

б) :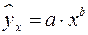

в) .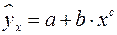

Ответ: в) .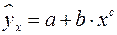

К внутренне нелинейным моделям можно отнести следующие модели: ,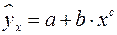

16. Какое из уравнений является степенным:

а) ;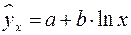

б) :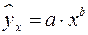

в) .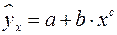

Ответ: б) :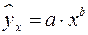

Существуют регрессии, нелинейные по оцениваемым параметрам, например

– степенная – .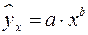

17. Параметр 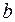в степенной модели является:

а) коэффициентом детерминации;

б) коэффициентом эластичности;

в) коэффициентом корреляции.

Ответ: б) коэффициентом эластичности;

Широкое использование степенной функции связано с тем, что параметр 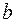в ней имеет четкое экономическое истолкование – он является коэффициентом эластичности. (Коэффициент эластичности показывает, на сколько процентов измениться в среднем результат, если фактор изменится на 1%.) Формула для расчета коэффициента эластичности имеет вид:

.

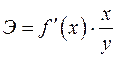Так как для остальных функций коэффициент эластичности не является постоянной величиной, а зависит от соответствующего значения фактора 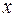, то обычно рассчитывается средний коэффициент эластичности:

.

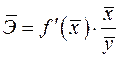18. Коэффициент корреляции 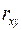может принимать значения:

а) от –1 до 1;

б) от 0 до 1;

в) любые.

Ответ: а) от –1 до 1

Линейный коэффициент корреляции находится в пределах: 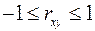. Чем ближе абсолютное значение 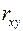к единице, тем сильнее линейная связь между факторами (при 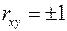имеем строгую функциональную зависимость). Но следует иметь в виду, что близость абсолютной величины линейного коэффициента корреляции к нулю еще не означает отсутствия связи между признаками. При другой (нелинейной) спецификации модели связь между признаками может оказаться достаточно тесной.

19. Для функции 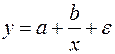средний коэффициент эластичности имеет вид:

а) ;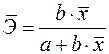

б) ;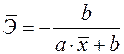

в) .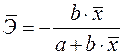

Ответ: б)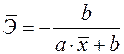

Вид функции,	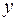Первая производная,	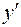Средний коэффициент эластичности,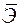

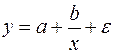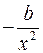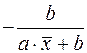20. Какое из следующих уравнений нелинейно по оцениваемым параметрам:

а) ;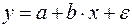

б) ;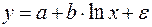

в) .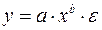

Ответ: в) .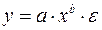

Среди нелинейных моделей наиболее часто используется степенная функция 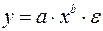, которая приводится к линейному виду логарифмированием:

;

;

,

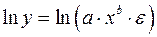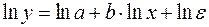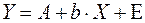где 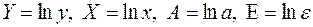. Т.е. МНК мы применяем для преобразованных данных:

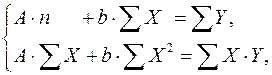
а затем потенцированием находим искомое уравнение.

Множественная регрессия и корреляция

1. Добавление в уравнение множественной регрессии новой объясняющей переменной:

а) уменьшает значение коэффициента детерминации;

б) увеличивает значение коэффициента детерминации;

в) не оказывает никакого влияние на коэффициент детерминации.

Ответ: б) увеличивает значение коэффициента детерминации

При дополнительном включении в регрессию фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться.

2. Скорректированный коэффициент детерминации:

а) меньше обычного коэффициента детерминации;

б) больше обычного коэффициента детерминации;

в) меньше или равен обычному коэффициенту детерминации;

Ответ: в) меньше или равен обычному коэффициенту детерминации

Скорректированный коэффициент множественной детерминации определяет тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов и поэтому может сравниваться по разным моделям с разным числом факторов.

В рассмотренных показателях множественной корреляции (индекс и коэффициент) используется остаточная дисперсия, которая имеет систематическую ошибку в сторону преуменьшения, тем более значительную, чем больше параметров определяется в уравнении регрессии при заданном объеме наблюдений . Если число параметров при равно 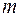и приближается к объему наблюдений, то остаточная дисперсия будет близка к нулю и коэффициент (индекс) корреляции приблизится к единице даже при слабой связи факторов с результатом. Для того чтобы не допустить возможного преувеличения тесноты связи, используется скорректированный индекс (коэффициент) множественной корреляции.

Скорректированный индекс множественной корреляции содержит поправку на число степеней свободы, а именно остаточная сумма квадратов 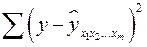делится на число степеней свободы остаточной вариации 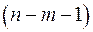, а общая сумма квадратов отклонений 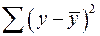на число степеней свободы в целом по совокупности .

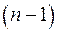Формула скорректированного индекса множественной детерминации имеет вид:

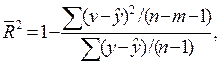
3. С увеличением числа объясняющих переменных скорректированный коэффициент детерминации:

а) увеличивается;

б) уменьшается;

в) не изменяется.

Ответ: б) уменьшается

Поскольку 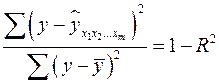, то величину скорректированного индекса детерминации можно представить в виде:

.

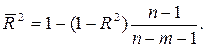Чем больше величина 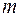, тем сильнее различия 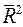и .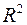

4. Число степеней свободы для остаточной суммы квадратов в линейной модели множественной регрессии равно:

а) ;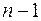

б) ;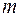

в) .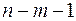

Ответ: в)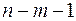

Компоненты дисперсии	Сумма квадратов	Число степеней свободы	Дисперсия на одну степень свободы
Остаточная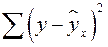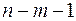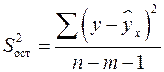

5. Число степеней свободы для общей суммы квадратов в линейной модели множественной регрессии равно:

а) ;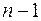

б) ;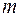

в) .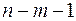

Ответ: а)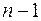

Компоненты дисперсии	Сумма квадратов	Число степеней свободы	Дисперсия на одну степень свободы
Общая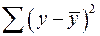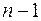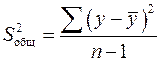

6. Число степеней свободы для факторной суммы квадратов в линейной модели множественной регрессии равно:

а) ;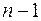

б) ;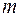

в) .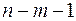

Ответ: б) m

Компоненты дисперсии	Сумма квадратов	Число степеней свободы	Дисперсия на одну степень свободы
Факторная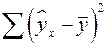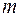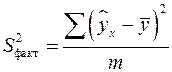

7. Множественный коэффициент корреляции 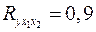. Определите, какой процент дисперсии зависимой переменной 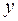объясняется влиянием факторов 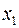и :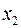

а) 90%;

б) 81%;

в) 19%.

Ответ: а) 90%

Процентное выражение дисперсии зависимой переменной y вычисляется:

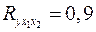; 0,9*100=90%

8. Для построения модели линейной множественной регрессии вида 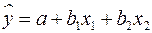необходимое количество наблюдений должно быть не менее:

а) 2;

б) 7;

в) 14.

Ответ: а) 2

В линейной множественной регрессии 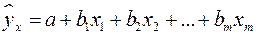параметры при 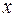называются коэффициентами «чистой» регрессии. Они характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне.

9. Стандартизованные коэффициенты регрессии :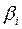

а) позволяют ранжировать факторы по силе их влияния на результат;

б) оценивают статистическую значимость факторов;

в) являются коэффициентами эластичности.

Ответ: а) позволяют ранжировать факторы по силе их влияния на результат

Ранжирование факторов, участвующих во множественной линейной регрессии, может быть проведено через стандартизованные коэффициенты регрессии ( 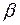-коэффициенты).

10. Частные коэффициенты корреляции:

а) характеризуют тесноту связи рассматриваемого набора факторов с исследуемым признаком;

б) содержат поправку на число степеней свободы и не допускают преувеличения тесноты связи;

в) характеризуют тесноту связи между результатом и соответствующим фактором при элиминировании других факторов, включенных в уравнение регрессии.

Ответ: в) характеризуют тесноту связи между результатом и соответствующим фактором при элиминировании других факторов, включенных в уравнение регрессии.

Частные коэффициенты корреляции характеризуют тесноту связи между результатом и соответствующим фактором при элиминировании (устранении влияния) других факторов, включенных в уравнение регрессии.

11. Частный 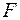-критерий:

а) оценивает значимость уравнения регрессии в целом;

б) служит мерой для оценки включения фактора в модель;

в) ранжирует факторы по силе их влияния на результат.

Ответ: б) служит мерой для оценки включения фактора в модель

Оценка значимости уравнения регрессии в целом производится на основе 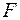-критерия Фишера, которому предшествует дисперсионный анализ. В математической статистике дисперсионный анализ рассматривается как самостоятельный инструмент статистического анализа. В эконометрике он применяется как вспомогательное средство для изучения качества регрессионной модели.

12. Несмещенность оценки параметра регрессии, полученной по МНК, означает:

а) что она характеризуется наименьшей дисперсией;

б) что математическое ожидание остатков равно нулю;

в) увеличение ее точности с увеличением объема выборки.

Ответ: б) что математическое ожидание остатков равно нулю

Несмещенность оценки означает, что математическое ожидание остатков равно нулю. Если оценки обладают свойством несмещенности, то их можно сравнивать по разным исследованиям.

13. Эффективность оценки параметра регрессии, полученной по МНК, означает:

а) что она характеризуется наименьшей дисперсией;

б) что математическое ожидание остатков равно нулю;

в) увеличение ее точности с увеличением объема выборки.

Ответ: а) что она характеризуется наименьшей дисперсией

Оценки считаются эффективными, если они характеризуются наименьшей дисперсией. В практических исследованиях это означает возможность перехода от точечного оценивания к интервальному.

14. Состоятельность оценки параметра регрессии, полученной по МНК, означает:

а) что она характеризуется наименьшей дисперсией;

б) что математическое ожидание остатков равно нулю;

в) увеличение ее точности с увеличением объема выборки.

Ответ: в) увеличение ее точности с увеличением объема выборки

Состоятельность оценок характеризует увеличение их точности с увеличением объема выборки

15. Укажите истинное утверждение:

а) скорректированный и обычный коэффициенты множественной детерминации совпадают только в тех случаях, когда обычный коэффициент множественной детерминации равен нулю;

б) стандартные ошибки коэффициентов регрессии определяются значениями всех параметров регрессии;

в) при наличии гетероскедастичности оценки параметров регрессии становятся смещенными.

Ответ: в) при наличии гетероскедастичности оценки параметров регрессии становятся смещенными.

16. При наличии гетероскедастичности следует применять:

а) обычный МНК;

б) обобщенный МНК;

в) метод максимального правдоподобия.

Ответ: а) обычный МНК

При использовании обобщенного МНК с целью корректировки гетероскедастичности коэффициент регрессии 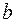представляет собой взвешенную величину по отношению к обычному МНК с весом .

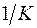17. Фиктивные переменные – это:

а) атрибутивные признаки (например, как профессия, пол, образование), которым придали цифровые метки;

б) экономические переменные, принимающие количественные значения в некотором интервале;

в) значения зависимой переменной за предшествующий период времени.

Ответ: а) атрибутивные признаки (например, как профессия, пол, образование), которым придали цифровые метки;

Чтобы ввести такие переменные в регрессионную модель, им должны быть присвоены те или иные цифровые метки, т.е. качественные переменные преобразованы в количественные. Такого вида сконструированные переменные в эконометрике принято называть фиктивными переменными.

18. Если качественный фактор имеет три градации, то необходимое число фиктивных переменных:

а) 4;

б) 3;

в) 2.

Ответ: в) 2

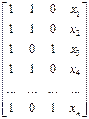
Предполагая при параметре 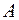независимую переменную, равную 1, имеем следующую матрицу исходных данных:

В рассматриваемой матрице существует линейная зависимость между первым, вторым и третьим столбцами: первый равен сумме второго и третьего столбцов. Поэтому матрица исходных факторов вырождена. Выходом из создавшегося затруднения может явиться переход к уравнениям

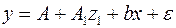
или

,

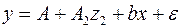т.е. каждое уравнение включает только одну фиктивную переменную 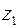или 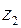.