Уравнения движения центра масс самолета

Самолет движется в воздухе по действием аэродинамической силы 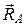, силы тяги двигателей 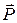и силы тяжести 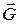. С аэродинамической силой и ее проекциями на оси различных систем координат мы познакомились при изучении основ аэродинамики. Сила тяги создается силовой установкой самолета. Вектор 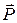обычно располагается в базовой плоскости самолета и образует некоторый угол с осью 0X связанной системы координат, но для простоты мы будем полагать, что этот угол равен нулю, а сам вектор 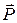приложен в центре масс.

Полет самолета можно условно разбить на несколько этапов: взлет, набор высоты, горизонтальный полет, снижение и посадка. Самолет также может совершать вираж и другие маневры. На некоторых этапах полета движение самолета может быть как установившимся, так и неустановившимся. При установившемся движении самолет летит с постоянной скоростью, при неизменных углах атаки, крена и скольжения. Ниже мы будем рассматривать только установившееся движение на этапах горизонтального полета, набора высоты и снижения.

Установившийся горизонтальный полет – это прямолинейный полет с постоянной скоростью на постоянной высоте (см. рис. 39). Уравнения движения центра масс самолета запишутся в этом случае следующим образом:

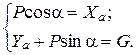(48)

Поскольку угол атаки a мал (при этом cos a » 1, а sin a » 0), то можно записать:

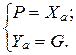(49)

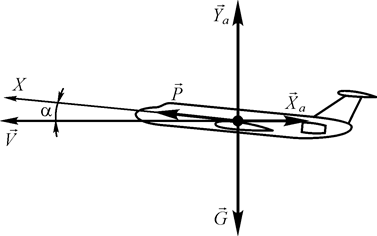
Рис. 39. Схема сил, действующих на самолет в установившемся

горизонтальном полете

Если первое из этих равенств не будет выполняться, то скорость самолета будет либо увеличиваться, либо уменьшаться, т.е. не будет выполняться условие установившегося движения. Если же подъемная сила не равна силе тяжести, то самолет будет либо подниматься, либо снижаться, а это значит, что не будет выполняться условие горизонтального полета. Из этого равенства, зная формулу подъемной силы (35), можно получить величину скорости, необходимую для выполнения горизонтального полета V_г.п.

Учитывая, что G = mg (где m – масса самолета, а g – ускорение свободного падения), можно записать:

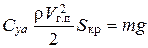, (50)

откуда:

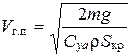(51)

Из этой формулы видно, что скорость горизонтального полета зависит от массы самолета, плотности воздуха r (которая зависит от высоты полета), площади крыла S_кр и коэффициента подъемной силы C_ya. Поскольку C_ya напрямую зависит от угла атаки a, то каждому значению скорости горизонтального полета будет соответствовать единственное значение угла атаки. Поэтому для обеспечения установившегося горизонтального полета с требуемой скоростью летчик задает определенную тягу двигателей и величину угла атаки.

Установившийся набор высоты – прямолинейное движение самолета вверх с постоянной скоростью. Схема сил, действующих на самолет при установившемся наборе высоты с углом наклона траектории q, показана на рис. 40.

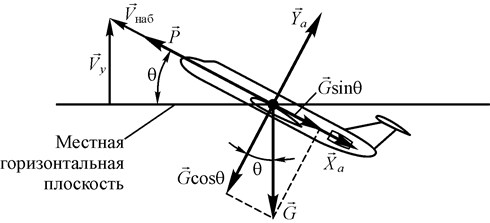
Рис. 40. Схема сил, действующих на самолет при установившемся

наборе высоты (угол атаки принят малым и не показан)

В этом случае уравнения движения примут вид:

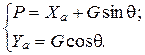(52)

Необходимо отметить, что при наборе высоты тяга двигателей P уравновешивает не только силу лобового сопротивления X_a, как в горизонтальном полете, но и составляющую силы тяжести Gsinq. Подъемная сила Y_a при этом требуется меньшая, поскольку Gcosq < G.

Важной характеристикой самолета является его скороподъемность – вертикальная скорость набора высоты V_y. Из рис. 40 видно, что:

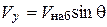. (53)

Установившееся снижение – прямолинейное движение самолета вниз с постоянной скоростью. На рис. 41 показана схема сил, действующих на самолет при снижении.

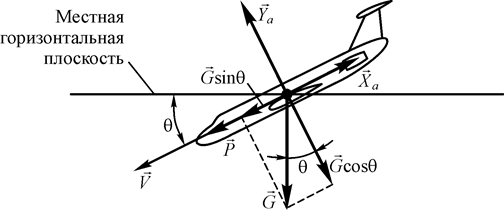
Рис. 41. Схема сил, действующих на самолет при установившемся

снижении (угол атаки принят малым и не показан)

Уравнения движения для установившегося снижения имеют вид:

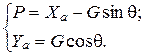(54)

Если мы поделим первое уравнение системы (54) на второе, то получим:

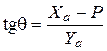. (55)

Из уравнения (55) видно, что установившееся снижение возможно только, если тяга меньше лобового сопротивления (P < X_a). Обычно снижение происходит при малых значениях тяги (при тяге малого газа), поэтому можно принять, что P » 0. Такой режим полета называется планированием. В этом случае:

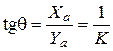. (56)

Важной характеристикой является дальность планирования L_пл с заданной высоты H_пл. Легко видеть, что:

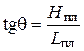, (57)

откуда:

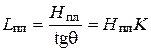. (58)

Из формулы (58) видно, что чем выше аэродинамическое качество самолета, тем больше будет дальность планирования.