Входное и выходное сопротивление четырехполюсника
Методы расчета параметров четырехполюсника:
1) Используя методы теории цепей, исключая параметры внутренних узлов и контуров схемы из уравнений;
2) По физическому смыслу – из опытов холостого хода и короткого замыкания.
Пример:
Рассчитаем Y-параметры П-образного четырехполюсника:
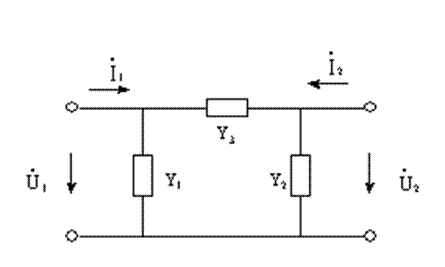
При коротком замыкании выхода:
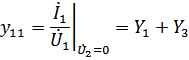
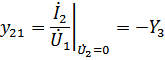
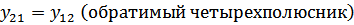
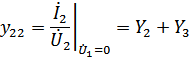
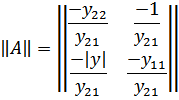
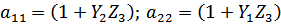
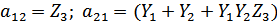
Для T-образной схемы параметры сопротивлений будут дуальными:
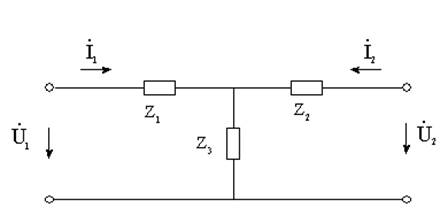
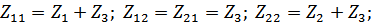
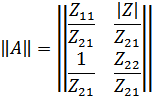
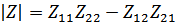
Получаем:
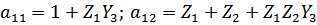
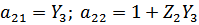
1.6 Соединения четырехполюсников.
Схема четырехполюсника сложной структуры может быть составлена из нескольких четырехполюсников более простой структуры путем соединения их выводов.
а) каскадное усиление
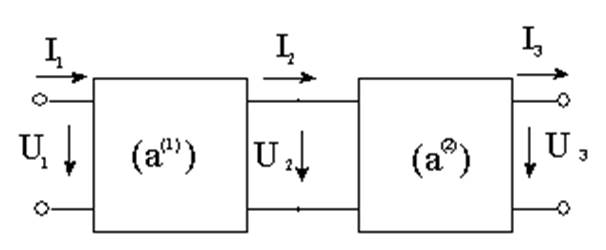
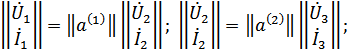
то есть
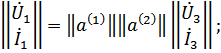
то есть
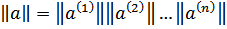
б) параллельное соединение
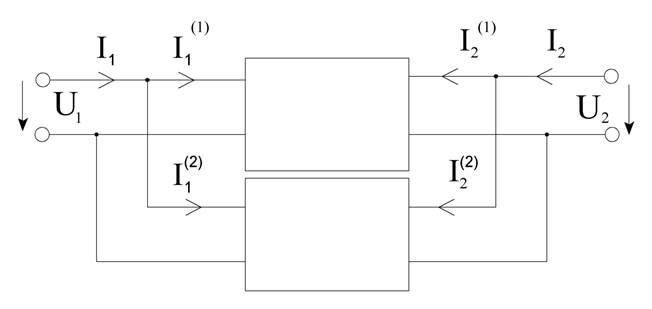
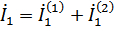
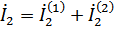
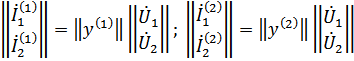
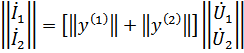
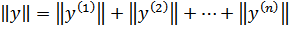
в) последовательное соединение
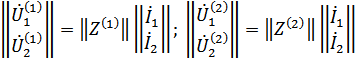
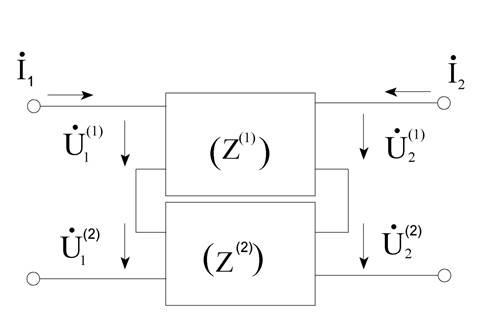
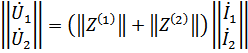
В общем случае
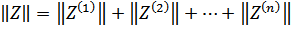
Анализ сложной схемы можно производить путем ее разбиения на более простые по структуре четырехполюсники.
Пример:
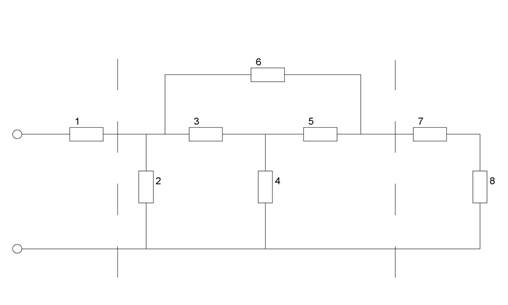
Средняя часть схемы: параллельно соединенный Т-образный четырехполюсник (3-4-5) и неуравновешенного четырехполюсника, состоящего из ветви (6) (выводы на входе и выходе нижние соединены между собой). К ним каскадно соединены два Г-образных четырехполюсника.
1.2 Функции передачи и функции входного сопротивления нагруженных четырехполюсников.
Изобразим схему нагруженного четырехполюсника
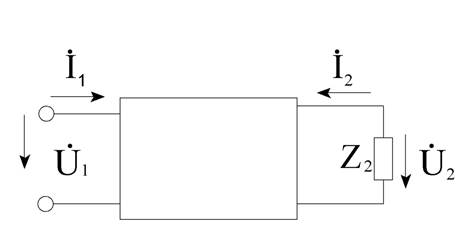
Z2 – двухполюсник нагрузки:
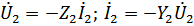
Функция передачи по напряжению
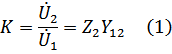
где 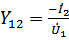 - передаточная проводимость четырехполюсника.
- передаточная проводимость четырехполюсника.
Функция передачи по току:
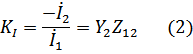
где 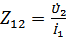 - передаточное сопротивление
- передаточное сопротивление
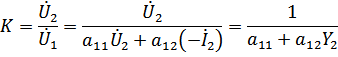
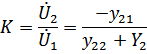
(связь a и y параметров)
Аналогично:
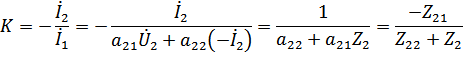
где 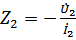
Функции передачи нагруженного четырехполюсника определяются только двумя его параметрами передачи
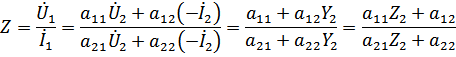
В частных случаях короткого замыкания (Z2=0) и разрыва (Y2=0) выхода четырехполюсника получаем входное сопротивление и входную проводимость
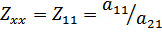
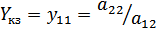
Функции цепи (то есть входные или передаточные), представляющей из себя четырехполюсник, состоящий из конечного числа элементов со сосредоточенными параметрами, является рациональной дробью от комплексной частоты:
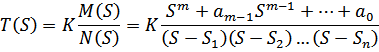
где Sk – полюса функции цепи или частоты собственных колебаний цепи. Докажем это.
Дифференциальное уравнение, связывающее напряжение и ток во входном контуре линейной цепи общего вида:
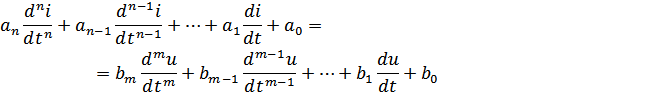
Пример: колебательный контур
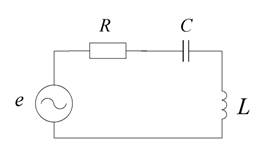
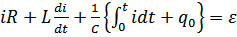
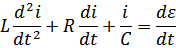
Комплексы напряжения и тока цепи:
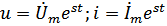
где S=α+jω – комплексная частота.
Они являются комплексными представлениями действительных сигналов в цепи:
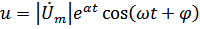
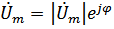
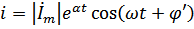
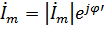
Подставляя u и i в уравнение, получим:
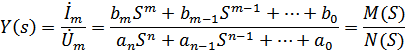
то есть комплексная функция цепи, в частности – входная проводимость, является рациональной дробью.
В зависимости от вида источника сигнала следует различать два случая свободного режима в цепи:
1) Режим короткого замыкания входных зажимов (при действии источника напряжения)
2) Режим разрыва входных зажимов (при действии источника тока)
В первом случае:
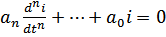 или
или
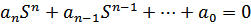 или
или
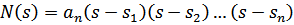
где Sk – корни характеристического уравнения, представляющие частоты собственных колебаний в режиме короткого замыкания входных зажимов.
Пример:
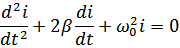
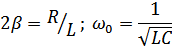
Подставим: 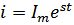
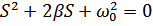
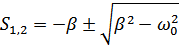
Если 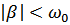
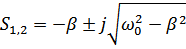
Собственные частоты (комплексные)
Для входного контура можно менять роли реакции и функции возбуждения. Поэтому во втором случае свободного режима
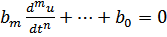 или
или
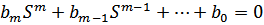 или
или
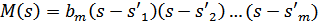
где s’k – корни характеристического уравнения, представляющие частоты собственных колебаний в режиме разрыва входных зажимов.
Вывод: комплексная функция цепи позволяет определять не только реакцию цепи в установившемся режиме, но также- и характеристическое уравнение свободного режима(её знаменатель содержит в себе частоты собственных колебаний цепи).
Перепишем выражение для комплексной входной проводимости:
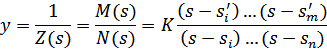
K= 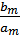
Частоты собственных колебаний цепи при разрыве: 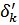 и коротком замыкании
и коротком замыкании 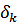 входных зажимов принято называть нулями и полюсами функции.
входных зажимов принято называть нулями и полюсами функции.
Нули входной проводимости являются полюсами входного сопротивления и обратно.
Проводимость передачи: 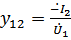
Определяем ток выхода при действии источника напряжения на входе.
Сопротивление передачи: 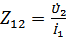
Определяем напряжение выхода при действии источника тока на входе.
Свободными режимами для них будут соответственно, режимы короткого замыкания и разрыва входных режимов.
Поэтому полюсы проводимости передачи совпадают с полюсами входной проводимости, а полюсы сопротивления передачи- совпадать с полюсами входного сопротивления, то есть с нулями входной проводимости.
Нули же функций передачи представляют те частоты, при которых передаваемый от входа к выходной ветви сигнал в виде тока или напряжения обращается в нуль.
Пример:
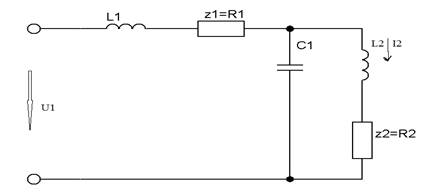
Ток и напряжение на выходе обращаются в нуль при тех s когда сопротивления последовательных ветвей стремится к бесконечности, а сопротивление параллельных ветвей стремится к нулю, соответственно:
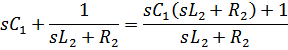

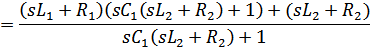
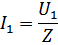
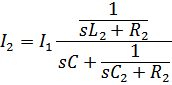
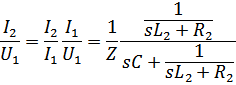
передаточная проводимость.
1.4. Характеристические параметры четырехполюсника: входное и выходное сопротивление, постоянная передачи.
Для расчета цепей каскадного соединения 4-полюсников вместо рассмотренных параметров можно использовать характеристические параметры, вводимые из теории цепей с распределёнными параметрами.
Для симметричных 4-полюсников вводятся два таких параметра: характеристическое сопротивление 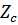 и характеристическая постоянная передачи
и характеристическая постоянная передачи 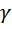 .
.
Характеристическое сопротивление представляет собой такое комплексное сопротивление, при включении которого в качестве нагрузки входное сопротивление 4-полюсника становится равным нагрузочному сопротивлению:
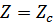
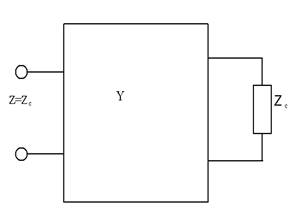
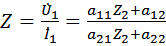
У нас 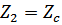 ,
, 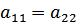
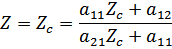
Т.е.
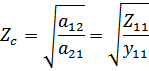
Вывод: характеристическое сопротивление равно среднему геометрическому из сопротивлений короткого замыкания и холостого хода:
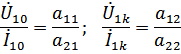
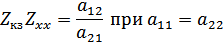
Характеристическая постоянная передачи 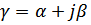 определяется функцией передачи 4-полюсника в режиме характеристической нагрузки; величина, обратная функции передачи напряжений или токов при
определяется функцией передачи 4-полюсника в режиме характеристической нагрузки; величина, обратная функции передачи напряжений или токов при 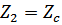 , принимается равной:
, принимается равной:
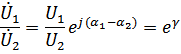
Постоянная передачи представляет собой натуральный логарифм от отношения комплексов напряжений(токов) на входе и выходе 4-полюсника:
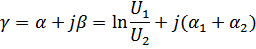
Её вещественная часть- характеристическое затухание α- представляет собой измеренное в логарифмическом масштабе отношение модулей напряжений(токов) на входе и выходе 4-полюсника, а мнимая составляющая 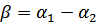 равна углу сдвига фазы между входным и выходным напряжениями(токами).
равна углу сдвига фазы между входным и выходным напряжениями(токами).
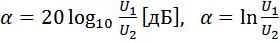
Было:
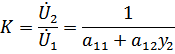
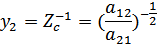
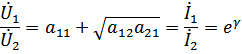
Т.е. постоянная передачисимметричного 4-полюсника для токов и напряжений одинакова и равна:
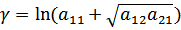
Характеристическое сопротивление и постоянная передачи полностью определяют поведение 4-полюсника, когда входное сопротивление и сопротивление нагрузки равны 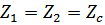 .
.
Выразим параметры передачи через характеристические параметры, называемые вторичными.
Было:
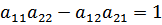
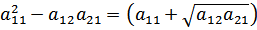
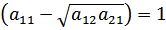
Но 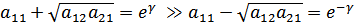
Сложение и вычитание даёт:
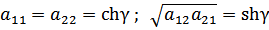
Но 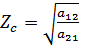
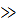
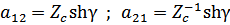
Запишем уравнение симметричного 4-полюсника через характеристические параметры:
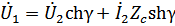
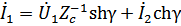
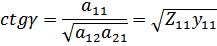
Гиперболический котангенс постоянной передачи равен квадратному корню из отношения сопротивлений холостого хода и короткого замыкания.
Под режимом согласования при каскадном соединении 4-полюсников понимают случай, когда характеристическое сопротивление на выходе предыдущего каскада равно характеристическому сопротивлению на входе последующего каскада, и сопротивление нагрузки равно характеристическому сопротивлению последнего каскада.
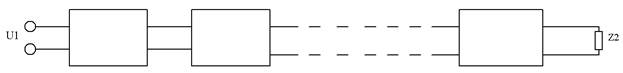
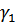
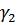
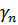
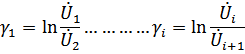
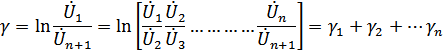
Т.е. затухание и фаза равны суммам затуханий и фаз отдельных звеньев.
В случае несимметричного 4-полюсника необходимо ввести три характеристических параметра: двахарактеристических сопротивления 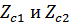 (входа и выхода) и постоянную передачи.
(входа и выхода) и постоянную передачи.


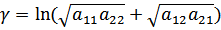
Характеристическое сопротивление представляется иррациональными выражениями. Их нельзя получить с помощью цепей, состоящих из конечного числа сосредоточенных элементов; сопротивление Z является рациональной дробью.
