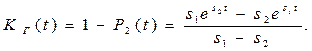Кафедра ИТАС

Контрольная работа

по дисциплине

«Надежность, эргономика и качество АСОИУ»

Выполнил: студент группы АСУ-01-з

Пименова Д.Н.

Проверил: Липатов И.Н.

Пермь 2006

Определение количественных характеристик надежности

по статистическим данным об отказах изделия.

Задача 1.9 В течение 1000 час из 10 гироскопов отказало 2. За интервал времени 1000 - 1100 час. отказал еще один гироскоп. Требуется определить f*(t), l*(t) при t =1000 час.

Решeниe.

f*(t) - статистическая оценка частоты отказов изделия

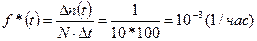
где Dn(t) - число отказавших изделий на участке времени (t, t+Dt);

Dt - интервал врeмени.

l*(t)- статистическая оценка интенсивности отказов изделия

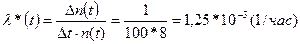
где n(t)- число изделий, не отказавших к моменту времени t; Dn(t) - число отказавших изделий на участке времени (t, t+Dt) .

Аналитическое определение количественных характеристик надёжности изделия.

Задача 2.8 Время работы изделия подчинено нормальному закону с параметрами m_t = 8000 час., s_t =1000 час. Требуется вычислить количественные характеристики надежности p(t) , f(t) , l(t) , m_t для t=8000 час.

Решeниe.

Воспользуемся формулами

,

,

,

,

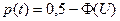
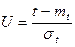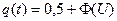
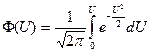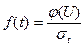
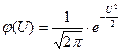для p(t), f(t), l(t),m_t.

1. Вычислим вероятность безотказной работы

p(t)=0.5-Ф(U) ; U=(t-m_t)/s_t ;

U=(8000-8000)/1000=0; Ф(0)=0;

p(8000)=0.5-0=0.5.

2. Определим частоту отказа f(t)

.

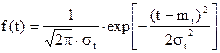Введем обозначение

.

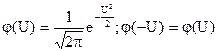Тогда

f(t)=j(U)/s_t ; U=(t-m_t)/s_t ;

f(8000)=j(0)/1000=0,3989/1000=39.89*10^-5 1/час.

3. Рассчитаем интенсивность отказов l(t)

l(t)=f(t)/p(t);

l(8000)=f(8000)/p(8000)=39.89·10^-5 /0.5=79.78·10^-5 1/час.

4. Среднее время безотказной работы элемента m_t =1/l=8000 час.

Последовательное соединение элементов в систему.

Задача 3.10 Система управления состоит из 6000 элементов, средняя интенсивность отказов которых l_ср. = 0,16*10^-6 1/час. Необходимо определить вероятность безотказной работы в течении t = 50 час и среднее время безотказной работы.

Решeниe.

Интенсивность отказов системы по формуле 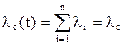будет

l_с=l_ср*n=0,16*10^-6*6000=0,96*10^-3 1/час.

Тогда на основании формулы

Р_c(t)= е^-lct

имеем

Р_c(50)= е^{-0,96*0,001*50} = е^-0,048 »0,953.

определим среднее время безотказной работы m_tc:

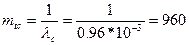часов.

Расчет надежности системы с постоянным резервированием.

Задача 4.6 В радиопередатчике, состоящем из трех равнонадежных каскадов (n=3) применено общее постоянное дублирование всего радиопередатчика. Интенсивность отказов каскада равна l=5*10^-4 1/час. Определить P_c(t), m_tc, f_c(t), l_c(t) радиопередатчика с дублированием.

Решeниe.

В данном случае n=3; l_i=l ; l₀=nl=3l;m=1.

По формуле P_c(t)=1-(1-e^-l0t)^m+1 имеем

Р_с(t)=1-(1-e^-3lt)^m+1;

.

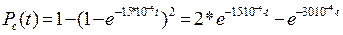Определим m_tс. Из формулы 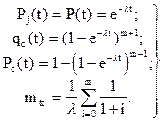имеем

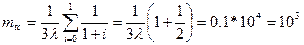час.

Определим частоту отказов f_c(t). Получим

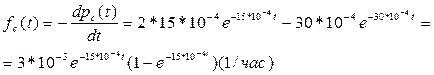
Определим интенсивность отказов l_с(t). Имеем:

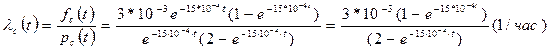
Резервирование замещением в режиме облегченного (теплого) резерва и в режиме ненагруженного (холодного) резерва.

Задача 5.6Схема расчета надежности системы приведена на рис. 5, где А,Б,В,Г – блоки системы. Определить вероятность безотказной работы P_c(t) системы.

А Б В Г

Рис. 5

Решeниe.

Вероятность безотказной работы системы равна:

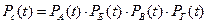
блок А – без резервирования (n=2);

блок Б – резервирование замещением в режиме ненагружаемого резерва;

блок В - без резервирования (n=1);

блок Г – режим постоянного резервирования (m=2).

Для блока А вероятность безотказной работы равна:

,

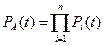где 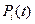- вероятности безотказной работы i-го элемента блока А.

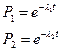
Тогда .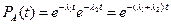

Для блока Б вероятность безотказной работы равна:

.

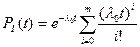Из условия задачи:

,

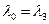m = 1.

Тогда .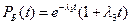

Для блока В вероятность безотказной работы равна:

,

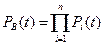где 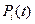- вероятности безотказной работы i-го элемента блока В.

.

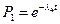Тогда .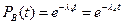

Для блока Г вероятность безотказной работы равна:

,

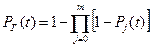где P_j - вероятности безотказной работы элемента резервного элемента j

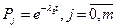
m =2.

Тогда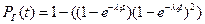

Найдем вероятности безотказной работы системы:

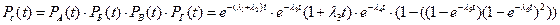
Ответ: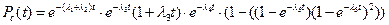

Расчет надежности системы с поэлементным резервированием.

Задача 6.7В телевизионном канале связи, состоящем из приемника и передатчика, применено раздельное дублирование передатчика и приемника. Передатчик и приемник имеют интенсивности отказов l_п=2*10^-3 1/час и l_пр=1*10^-3 1/час соответственно. Схема канала представлена на рис. 6. Требуется определить вероятность безотказной работы канала P_c(t) , среднее время безотказной работы m_tc, частоту отказов f_c(t) , интенсивность отказов l_с(t).

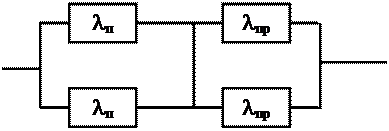Рис. 6

Решeниe.

Вероятность безотказной работы системы равна:

,

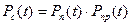где P_п(t), P_пр(t) - вероятности безотказной работы передатчика и приемника (с резервированием).

Для передатчика вероятность безотказной работы равна:

,

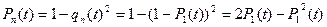где P₁ - вероятности безотказной работы резервного элемента передатчика.

Для приемника вероятность безотказной работы равна:

,

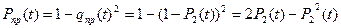где P₂ - вероятности безотказной работы резервного элемента передатчика.

Найдем вероятность безотказной работы системы:

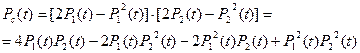
Из условия задачи:

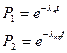
Тогда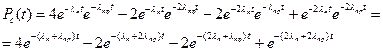

Подставим исходные данные:

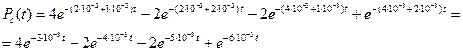
Найдем частоту отказов.

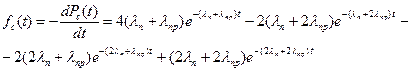
Подставим исходные данные:

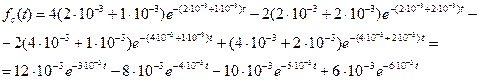
Найдем интенсивность отказов:

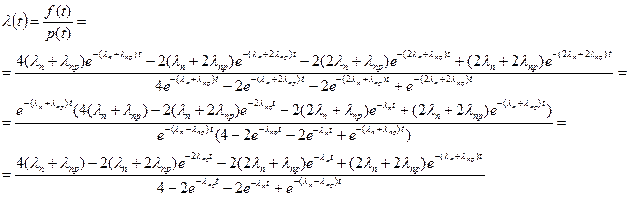
Подставим исходные данные:

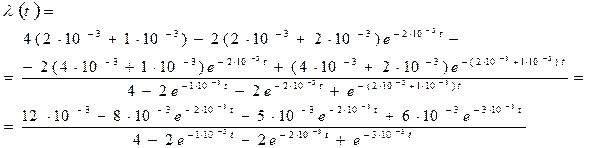
Найдем среднее время безотказной работы:

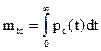
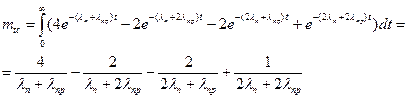
Подставим исходные данные:

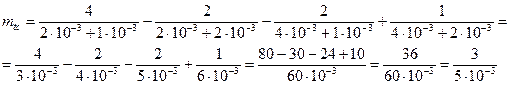
Ответ:

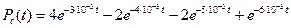
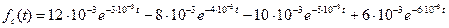
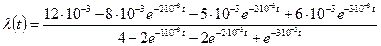
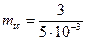
Резервирование с дробной кратностью и постоянно включенным резервом.

Задача 7.5Автомобильный двигатель имеет l=4 свечи зажигания по одной на каждый цилиндр. Интенсивность отказов свечи l=10^-3 1/час, а длительность работы двигателя в течение всего путешествия t=20 час. Предполагается, что автомобиль может ехать также при одном неработающем цилиндре. Необходимо определить вероятность безотказной работы двигателя P_c(t), среднее время безотказной работы двигателя m_tc , частоту отказов f_c(t), интенсивность отказов l_c(t) двигателя. Какова вероятность того, что автомобиль доставит туристов в пункт назначения без замены свечей?

Решeниe.

Найдем вероятность безотказной работы устройства P_c (t) :

,

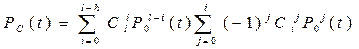где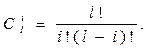

Р_о(t) - вероятность безотказной работы основной системы или любой резервной системы; l - общее число основных и резервных систем; h - число систем, необходимых для нормальной работы.

Из условия задачи:

l = 4

h = 3

Тогда

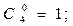
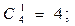
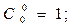
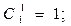
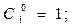
Будем предполагать, что для любой отдельно взятой системы справедлив экспоненциальный закон надежности, т.е.

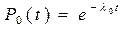
Тогда

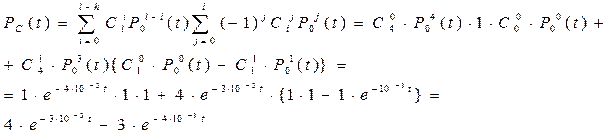
Для данных нашей задачи 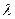t = 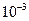*20=0,02.

Тогда

P_c(20)= .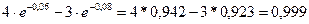

Среднее время безотказной работы на основании формулы (7.4) будет:

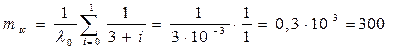час.

Определим частоту отказов f_c(t). Имеем

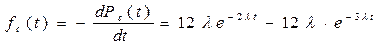
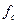(20)= 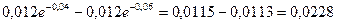(1/час)

Определим интенсивность отказов l_с(t). Получим

.

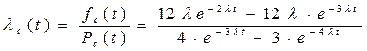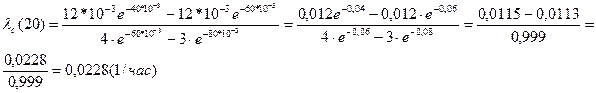
Скользящее резервирование при экспоненциальном законе надежности.

Задача 8.5Бортовая аппаратура спутника включает в себя аппаратуру связи, командную и телеметрическую системы, систему питания и систему ориентации. Аппаратура связи состоит из двух работающих ретрансляторов и одного ретранслятора в ненагруженном резерве. Переключающее устройство предполагается абсолютно надежным. Командная система имеет постоянное резервирование. Системы питания, ориентации и телеметрии резерва не имеют. Заданы интенсивности отказа: каждого комплекта ретранслятора - l ₁ , командной системы - l ₂ , системы телеметрии - l ₃ , системы питания - l ₄ и системы ориентации - l ₅ . Требуется определить вероятность безотказной работы P_c(t) бортовой аппаратуры спутника. Логическая схема для расчета надежности бортовой аппаратуры спутника представлена на рис. 8. Здесь I - аппаратура ретранслятора, II - командная система, III - остальные системы.

I II III

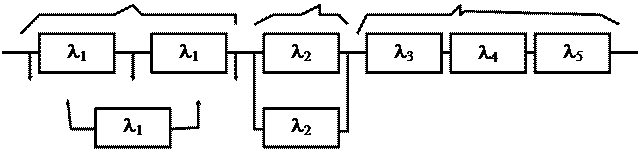Рис. 8

Решeниe.

Вероятность безотказной работы системы равна:

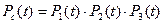
блок 3 – без резервирования (n=3);

блок 1 – резервирование замещением в режиме ненагружаемого резерва;

блок 2 – режим постоянного резервирования (m=1).

Для блока 1 вероятность безотказной работы равна:

.

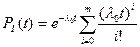Из условия задачи:

,

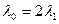m = 1.

Тогда .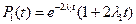

Для блока 2 вероятность безотказной работы равна:

,

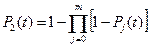где P_j - вероятности безотказной работы элемента резервного элемента j

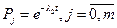
m =1.

Тогда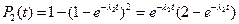

Для блока 3 вероятность безотказной работы равна:

,

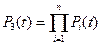где 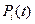- вероятности безотказной работы i-го элемента блока 3.

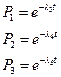
Тогда .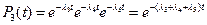

Найдем вероятности безотказной работы системы:

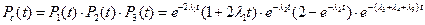
Ответ: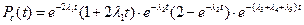

Расчет показателей надежности резервированных устройств с учетом восстановления.

Задача 9.11Система связи содержит одно устройство, предназначенное для выполнения задачи и одно устройство в нагруженном резерве. Интенсивность отказов каждого устройства равна l 1/час , восстановления - m 1/час . Ремонт устройств производится независимо друг от друга. Определить функцию готовности.

Решeниe.

2l l

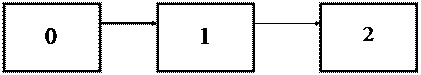
m 2m

Рис. 9

Вычислительное устройство в любой момент времени может находиться в одном из следующих состояний:

0 - оба блока работоспособны;

1 - один блок неработоспособен;

2 - оба блока неработоспособны.

Схема состояний устройства представлена на рис.9. Определяем вероятность непрерывной безотказной работы в течении времени t . Система дифференциальных уравнений, полученная по схеме состояний, имеет следующий вид:

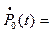-lP₀(t) + mP₁(t) ;

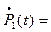lP₀(t) - (l + m)P₁(t) ;

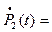lP₁(t) .

Начальные условия:

P₀(0) = 1 ; P₁(0) = P₂(0) = 0 .

При помощи преобразования Лапласа получаем систему алгебраических уравнений относительно изображений:

(s+l)P₀(s) - mP₁(s) = 1 ;

-lP₀(s) + (s + l + m)P₁(s) = 0 ;

-lP₁(s) + sP₂(s) = 0 .

Путем решения этой системы либо подстановкой, либо по правилу Крамера получим

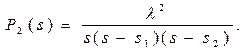
Раскладывая P₂(s) на элементарные дроби и производя обратное преобразование Лапласа, определяем вероятность P₂(t) попадания за время (0 , t) в состояние 2

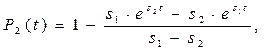
где обозначено

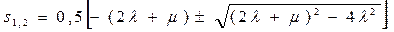
Следовательно, вероятность непрерывной безотказной работы вычислительного устройства за время (0 , t) равна