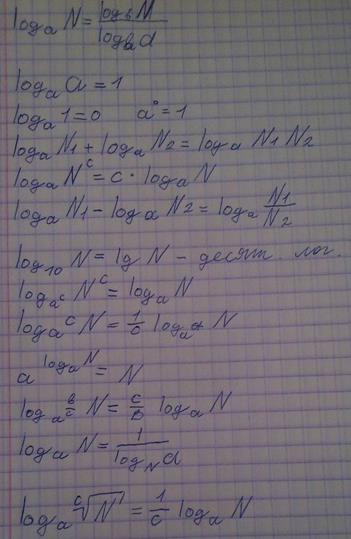Свойства степени с рациональным показателем
Свойства степеней
Основные свойства степеней с целым показателем:
am *an = a(m+n);
am : an = a(m-n) ( при a не равном нулю);
(am)n = a(m*n);
(a*b)n = an *bn;
(a/b)n = (an)/(bn) (при b не равном нулю);
a1 = a;
a0 = 1 ( при a не равном нулю);
Эти свойства будут справедливы для любых чисел a, b и любых целых чисел m и n. Стоит отметить также следующее свойство:
Если m>n, то am > an, при a>1 и am
Можно обобщить понятие степени числа на случаи, когда в качестве показателя степени выступают рациональные числа. При этом хотелось бы, чтобы выполнялись все выше перечисленные свойства или хотя бы часть из них.
Например, при выполнении свойства (am)n = a(m*n) выполнялось бы следующее равенство:
(a(m/n))n = am.
Это равенство означает, что число a(m/n) должно являться корнем n-ой степени из числа am.
Степенью некоторого числа a (большего нуля) с рациональным показателем r = (m/n), где m – некоторое целое число, n – некоторое натурально число большее единицы, называется число n√(am). Исходя из определения: a(m/n) = n√(am).
Для всех положительных r будет определена степень числа нуль. По определению 0r = 0. Отметим также, что при любом целом, любых натуральных m и n, и положительном а верно следующее равенство: a(m/n) = a((mk)/(nk)).
Например: 134(3/4) = 134(6/8) = 134(9/12).
Из определения степени с рациональным показателем напрямую следует тот факт, что для любого положительного а и любого рационального r число ar будет положительным.
Тождественные преобразования выражений, содержащих степень с рациональным показателем.
Степени с действительными показателями
Пусть дано положительное число 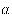 и произвольное действительное число
и произвольное действительное число 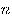 . Число
. Число 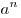 называется степенью, число
называется степенью, число 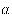 — основанием степени, число
— основанием степени, число 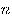 — показателем степени.
— показателем степени.
По определению полагают:
-
 .
. -
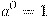 .
. -
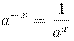 ,
, 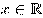 .
.
Если 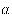 и
и 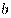 — положительные числа,
— положительные числа, 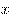 и
и 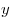 — любые действительные числа, то справедливы следующие свойства:
— любые действительные числа, то справедливы следующие свойства:
-
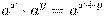 .
. -
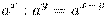 .
. -
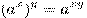 .
. -
 .
. -
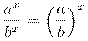 .
. -
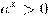 .
.
Свойства степени с действительным показателем
Свойства степени с действительным показателем
На степени с действительными показателями переносятся все свойства степеней с рациональными показателями.
1) 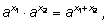
2) 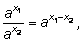
3) 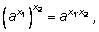
4) 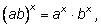
5) 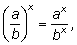
6) 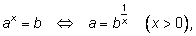
7) 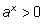 при любом действительном x,
при любом действительном x,
8) пусть 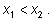 Если
Если 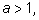 то
то 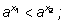 если
если 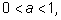 то
то 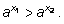
Понятие логарифма числа
Логарифмом числа
B по основанию a называется показатель степени, в которую надо возвести основание a, чтобы получилось число b.
Обозначение:
loga b.
Читаем: "логарифм от b по основанию a".
Основное логарифмическое тождество
Это основное логарифмическое тождество.
Это тождество следует из определения логарифма: так как логарифм – это показатель степени (n), то, возводя в эту степень число а, получим число b.
Основные свойства логарифмов
Основные свойства логарифмов