Погрешности косвенных измерений

Задача ставится так: пусть искомая величина z определяется через другие величины a, b, c, ..., полученные при прямых измерениях

z = f (a, b, c,...) (1.11)

Необходимо найти среднее значение функции и погрешность ее измерений, т.е. найти доверительный интервал

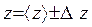(1.12)

при надежности a и относительную погрешность .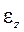

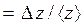Что касается 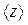, то оно находится путем подстановки в правую часть (11) вместо a, b, c,... их средних значений

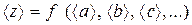. (1.13)

Абсолютная погрешность косвенных измерений 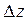является функцией абсолютных погрешностей прямых измерений и вычисляется по формуле

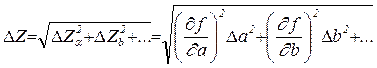(1.14)

Здесь 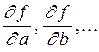частные производные функции f по переменным a, b, …

Если величины a, b, c, ... в функцию Z = f (a, b, c,...) входят в виде сомножителей в той или иной степени, т. е. если

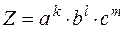, (1.15)

то сначала удобно вычислить относительную погрешность

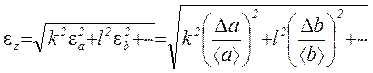, (1.16)

а затем абсолютную

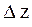
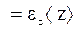(1.17)

Формулы для Dz и e_z приводятся в справочной литературе.

Примечания.

1. При косвенных измерениях в расчетные формулы могут входить известные физические константы (ускорение свободного падения g, скорость света в вакууме с и т. д.), числа типа 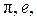дробные множители 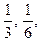... . Эти величины при вычислениях округляются. При этом, естественно, в расчет вносится погрешность 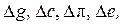‒ погрешность округления при вычислениях, которая должна учитываться.

Принято считать, что погрешность округления приближенного числа равна половине единицы того разряда, до которого это число было округлено. Например,p = 3,14159... . Если взять p= 3,1, то Dp = 0,05, если p = 3,14, то Dp = 0,005 ... и т.д. Вопрос о том, до какого разряда округлять приближенное число, решается так: относительная ошибка, вносимая округлением, должна быть того же порядка или на порядок меньше, что и максимальная из относительных ошибок других видов. Таким же образом оценивается абсолютная ошибка табличных данных. Например, в таблице указано r = 13,6×10³ кг/ м³, следовательно,Dr = 0,05×10³ кг/м³.

Ошибка значений универсальных постоянных часто указывается вместе с их принятыми за средние значения: (с = 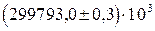м/c, где Dс = 0,3×10³ м/c.

2. Иногда при косвенных измерениях условия опыта при повторных наблюдениях не совпадают. В этом случае значение функции z вычисляется для каждого отдельного измерения, а доверительный интервал вычисляется через значения z так же, как при прямых измерениях (все погрешности здесь входят в одну случайную погрешность измерения z). Величины, которые не измеряются, а задаются (если они есть) должны быть указаны при этом с достаточно большой точностью.

Порядок обработки результатов измерений

Прямые измерения

1. Вычислить среднее значение для n измерений

.

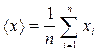2. Найти погрешности отдельных измерений .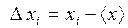

3. Вычислить квадраты погрешностей отдельных измерений и их сумму: .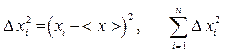

4. Задать надежностьa (для наших целей принимаем a = 0,95) и по таблице определить коэффициенты Стьюдента t_a,nи t_a,¥.

5. Произвести оценку систематических погрешностей: приборной Dх_пр и ошибки округления при измеренияхDх_окр= D/2 (D ‒ цена деления прибора) и найти полную погрешность результата измерений (полуширину доверительного интервала):

.

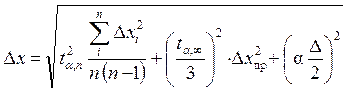6. Оценить относительную погрешность

.

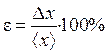7. Окончательный результат записать в виде

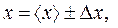ε = … % при a = ...

Косвенные измерения

1. Для каждой величины, измеренной прямым способом, входящей в формулу для определения искомой величины 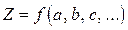, провести обработку, как указано выше. Если среди величин a, b, c, ... есть табличные константы или числа типа p, е,..., то при вычислениях 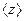округлять их следует так (если это возможно), чтобы вносимая при этом относительная ошибка была на порядок меньше наибольшей относительной ошибки величин, измеренных прямым способом.

Определить среднее значение искомой величины

z = f (<a>,<b>,<c>,...).

3. Оценить полуширину доверительного интервала для результата косвенных измерений

,

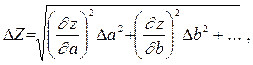где производные 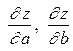... вычисляются при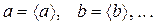

4. Определить относительную погрешность результата

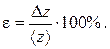
5. Если зависимость z от a, b, c,... имеет вид 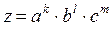, где k, l, m ‒ любые действительные числа, то сначала следует найти относительную ошибку

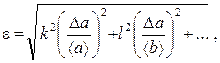
а затем абсолютную .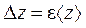

6. Окончательный результат записать в виде

z = <z> ± Dz , ε = …% при a=… .

Примечание:

При обработке результатов прямых измерений нужно следовать следующему правилу: численные значения всех рассчитываемых величин должны содержать на один разряд больше, чем исходные (определенные экспериментально) величины.

При косвенных измерениях вычисления 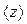производить по правилам приближенных вычислений:

Правило 1. При сложении и вычитании приближенных чисел необходимо:

а) выделить слагаемое, у которого сомнительная цифра имеет наиболее высокий разряд;

б) все остальные слагаемые округлить до следующего разряда (сохраняется одна запасная цифра);

в) произвести сложение (вычитание);

г) в результате отбросить последнюю цифру путем округления (разряд сомнительной цифры результата при этом совпадает со старшим из разрядов сомнительных цифр слагаемых).

Пример: 5,4382·10⁵ – 2,918·10³ + 35,8 + 0,064.

В этих числах последние значащие цифры сомнительные (неверные уже отброшены). Запишем их в виде 543820 – 2918 + 35,8 + 0,064.

Видно, что у первого слагаемого сомнительная цифра 2 имеет наиболее высокий разряд (десятки). Округлив все другие числа до следующего разряда и сложив, получим

543820 – 2918 + 36 + 0 = 540940 = 5,4094·10⁵.

Правило 2. При умножении (делении) приближенных чисел необходимо:

а) выделить число (числа) с наименьшим количеством значащих цифр (ЗНАЧАЩИЕ – цифры отличные от ноля и ноли стоящие между ними);

б) округлить остальные числа так, чтобы в них было на одну значащую цифру больше (сохраняется одна запасная цифра), чем выделенном по п. а;

в) перемножить (разделить) полученные числа;

г) в результате оставить столько значащих цифр, сколько их было в числе (числах) с наименьшим количеством значащих цифр.

Пример: .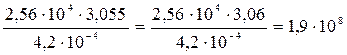

Правило 3. При возведении в степень, при извлечении корня в результате сохраняется столько значащих цифр, сколько их в исходном числе.

Пример: .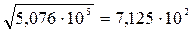

Правило 4. При нахождении логарифма числа мантисса логарифма должна иметь столько значащих цифр, сколько их в исходном числе:

Пример: .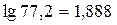

В окончательной записиабсолютной погрешности следует оставлять только одну значащую цифру. (Если этой цифрой окажется 1, то после нее сохраняют еще одну цифру).

Среднее значение округляется до того же разряда, что и абсолютная погрешность.

Например: V = (375,21 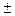0,03) см³ = (3,7521 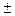0,0003) см³.

I = (5,530 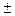0,013) А, A = 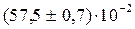Дж.

Порядок выполнения работы

Определение диаметра цилиндра.

1. Штангенциркулем измерить 7 раз (в разных местах и направлениях) диаметр цилиндра. Результаты записать в таблицу.

№ п/п	di , мм	di - <d>	(di -<d>)2	hi, мм	hi - < h>	(hi - <h>)2
	23,4 23,8 24,0 23,3 23,6 23,5 23,3	-0,2 0,2 0,6 -0,3 0,0 -0,1 -0,3	0,04 0,04 0,36 0,09 0,01 0,09	58,0 58,2 58,3 58,2 58,1 58,3 58,3	0,0 0,0 -0,1 0,0 0,1 -0,1 -0,1	0,04 0,01 0,01 0,01 0,01
Сумма	164,9		0,63	407,6		0,08
Среднее значение	23,6			58,2

2. Вычислить среднее значение диаметра:

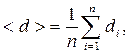
где n - число измерений, i - номер измерения.

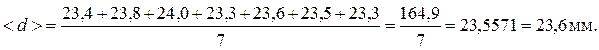
3. Вычислить Dd_i = (d_i - <d>), Dd_i²и 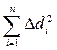и записать в таблицу.

Например: Dd₁= (23,4 – 23,6) = ‒0,2; 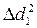= (‒0,2)² = 0,04

4. Задавшись надежностью a (от 0,90 до 0,97), по таблице выбрать коэффициенты Стьюдента t_a,n и t_a,¥. По ГОСТу в большинстве случаев a = 0,95, n = 7. Тогда t_a,n = 2,45, t_a,¥ = 1,96.

5. Определить приборную погрешность Dd_пр. Для микрометраDd_пр = D/2 (D - цена деления микрометра, равная обычно 0,01 мм). Для штангенциркуля Dd_пр = D, D - “цена” деления нониуса. Если нониус штангенциркуля имеет 10 делений, то Dd_пр = D = 0,1 мм.

6. Вычислить абсолютную ошибку (полуширину доверительного интервала) в определении диаметра цилиндра:

.

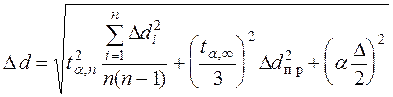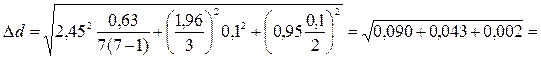
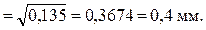
d = (23,6 ± 0,4) мм.

7. Вычислить относительную погрешность диаметра.

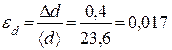или e_d = 1,7%