Гомоскедастичность и гетероскедастичность остатков модели регресиии

Гетероскедастичность

Случайной ошибкой называется отклонение в линейной модели множественной регрессии:

εi=yi–β0–β1x1i–…–βmxmi

В связи с тем, что величина случайной ошибки модели регрессии является неизвестной величиной, рассчитывается выборочная оценка случайной ошибки модели регрессии по формуле:

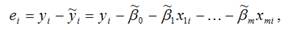
где ei – остатки модели регрессии.

Термин гетероскедастичность в широком смысле понимается как предположение о дисперсии случайных ошибок модели регрессии.

При построении нормальной линейной модели регрессии учитываются следующие условия, касающиеся случайной ошибки модели регрессии:

6) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:

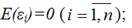
7) дисперсия случайной ошибки модели регрессии постоянна для всех наблюдений:

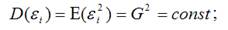
8) между значениями случайных ошибок модели регрессии в любых двух наблюдениях отсутствует систематическая взаимосвязь, т. е. случайные ошибки модели регрессии не коррелированны между собой (ковариация случайных ошибок любых двух разных наблюдений равна нулю):

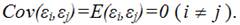
Второе условие

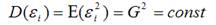
означает гомоскедастичность (homoscedasticity – однородный разброс) дисперсий случайных ошибок модели регрессии.

Под гомоскедастичностью понимается предположение о том, что дисперсия случайной ошибки βi является известной постоянной величиной для всех наблюдений.

Но на практике предположение о гомоскедастичности случайной ошибки βi или остатков модели регрессии ei выполняется не всегда.

Под гетероскедастичностью (heteroscedasticity – неоднородный разброс) понимается предположение о том, что дисперсии случайных ошибок являются разными величинами для всех наблюдений, что означает нарушение второго условия нормальной линейной модели множественной регрессии:

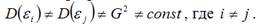
Гетероскедастичность можно записать через ковариационную матрицу случайных ошибок модели регрессии:

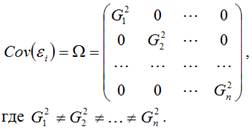
Тогда можно утверждать, что случайная ошибка модели регрессии βi подчиняется нормальному закону распределения с нулевым математическим ожиданием и дисперсией G2Ω:

εi~N(0; G2Ω),

где Ω – матрица ковариаций случайной ошибки.

Если дисперсии случайных ошибок

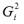
модели регрессии известны заранее, то проблема гетероскедастичности легко устраняется. Однако в большинстве случаев неизвестными являются не только дисперсии случайных ошибок, но и сама функция регрессионной зависимости y=f(x), которую предстоит построить и оценить.

Для обнаружения гетероскедастичности остатков модели регрессии необходимо провести их анализ. При этом проверяются следующие гипотезы.

Основная гипотеза H0 предполагает постоянство дисперсий случайных ошибок модели регрессии, т. е. присутствие в модели условия гомоскедастичности:

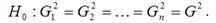
Альтернативная гипотеза H1 предполагает непостоянство дисперсиий случайных ошибок в различных наблюдениях, т. е. присутствие в модели условия гетероскедастичности:

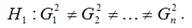
Гетероскедастичность остатков модели регрессии может привести к негативным последствиям:

1) оценки неизвестных коэффициентов нормальной линейной модели регрессии являются несмещёнными и состоятельными, но при этом теряется свойство эффективности;

2) существует большая вероятность того, что оценки стандартных ошибок коэффициентов модели регрессии будут рассчитаны неверно, что конечном итоге может привести к утверждению неверной гипотезы о значимости коэффициентов регрессии и значимости модели регрессии в целом.

Гомоскедастичность

Гомоскедастичность остатков означает, что дисперсия каждого отклонения одинакова для всех значений x. Если это условие не соблюдается, то имеет место гетероскедастичность. Наличие гетероскедастичности можно наглядно видеть из поля корреляции.

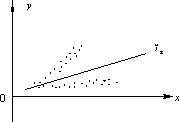
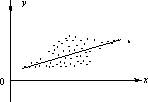
Т.к. дисперсия характеризует отклонение то из рисунков видно, что в первом случае дисперсия остатков растет по мере увеличения x, а во втором – дисперсия остатков достигает максимальной величины при средних значениях величины x и уменьшается при минимальных и максимальных значениях x. Наличие гетероскедастичности будет сказываться на уменьшении эффективности оценок параметров уравнения регрессии. Наличие гомоскедастичности или гетероскедастичности можно определять также по графику зависимости остатков от теоретических значений 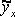.