Лекция №7. Айнымалы тоқ және оның параметрлері: периоды, жиілігі және т.б

Уақытша диаграммалар.

Жоспар

1. Айнымалы тоқ туралы мағлұмат
2. Айнымалы тоқтың параметрлері: периоды, жиілігі және т.б.
3. Уақытша диаграммалар

Айталау

§ Электр тоғы, металдардағы электр тоғы, сұйықтардағы электр тоғы, газдардағы электр тоғы, вакуумдегі электр тоғы және т.б. Тұрақты тоқ- бағыты және шамасы іс-жүзінде уақыт өтсе де өзгермейтін тоқ.

Айнымалы тоқ, (ағылшынша alternating current – айнымалы тоқ) – бағыты мен шамасы периодты түрде өзгеріп отыратын электр тоғы. Ал техникада айнымалы тоқ деп тоқ күші мен кернеудің период ішіндегі орташа мәні нөлге тең болатын периодты тоқ болады. Айнымалы тоқ байланыс құрылғыларында (радио, теледидар, телефон т.б.) кеңінен қолданылады.

Айнымалы токты пайдаланудың ең алғаш рет 1875 жылы орыс ғалымы П.Н.Яблочков ұсынды. Айнымалы ток Яблочков шырағындағы көмірдің біркелкі жануын қамтамасыз етті және шамдардың бір электр энергиясы көзінен қоректенуіне жол ашты.

Электр энергиясы қажеттілігінің өсуіне байланысты оны алыс қашықтыққа жеткізу мәселесі алға қойылды. Бұл мәселенің шешімі электр энергиясын таратуды, ол үшін әртүрлі кернеуді табуды талап етті. Үнемділік жағынан алғанда, электр энертиясын алыс қашықтықтарға жеткізудегі тиімдісі – жоғары кернеу, ал қабылдағыштарға беру кезінде қауіпсіздік ережелерін сақтау үшін төменгі кернеу қажет болды.

Кернеуді бұдан былай түрлендіру үшін, айнымалы токты түрлендіретін құрылғы, яғни қарапайым трансформаторлар қажет болды, оны да өзінің шырақтары үшін Яблочков ойлап тапты.

Одан кейін атақты орыс инженері және ғалымы М.О.Доливо – Добровольскийдің басшылығымен үш фазалы жүйе ойлап шығарылды. М.О.Доливо – Добровольскийдің арқасында айнымалы ток кеңінен тарады. 1889 жылы ол бірінші рет фазалы қозғалтқыш және үш фазалы тізбектің барлық тетіктерін жасап шығарды. 1891 жылы ол электр энергиясын үш фазалы токпен 175 шақырым қашықтыққа жеткізуді іске асырды.

Айнымалы токты электротехника саласында кеңінен пайдалану орталықтандырылған түрде электр энергиясын өндіруді, алыс қашықтыққа жеткізуді, оны таратуды және қабылдауды игерген кезеңнен басталды.

Айнымалы токқа қатысты ұғымдармен танысайық.

Айнымалы ток деп уақытқа байланысты шамасы мен бағыты өзгеріп отыратын токты айтамыз. Айнымалы токтың кез келген аз уақыт мезгіліндегі мәнін лездік ток деп атайды, оны i әрпімен белгілейді. Лездік токтың (і) зарядқа және уақытқа қатысты екендігі мына қатынастан көрінеді:

i = dq / dt. (1)

0 – ден t – ға дейінгі уақыт аралығында айнымалы ток мынандай заряд тасиды:

q = ∫ i dt.

Халықаралық СИ жүйесі бойынша ток күшінің бірлігі ретінде ампер (А) алынған. Бұл жүйеде заряд ампер – секундпен немесе кулонмен өлшенеді. 1 кулон (Кл) заряд 6,29 * 10¹⁸ электрон зарядына тең. Егер ток күші 1 ампер болса, онда бұл - өткізгіштің көлденең қимасы арқылы секундына 6,29 * 10¹⁸ электрон ағып өтеді деген сөз.

Егер лездік токтың уақытқа тәуелділігі белгілі болса, i = F(t) және оның бағыты көрсетілсе, онда токты белгілі деп есептеуге болады. Айнымалы токтың пішіні әртүрлі, соның ішінде көп тарағандарының бірі – периодты токтар.

Периодты токтар деп токтың лездік мәндері бірдей уақыт аралықтарында қайталанып отыратын токтарды айтамыз. Ал тоқтың лездік мәні қайталанып отыратын ең аз уақыты сол токтың периоды деп аталады, оны Т әрпімен белгілейді. Периодтық ток үшін:

i = F(t) = F(t+T) (2)

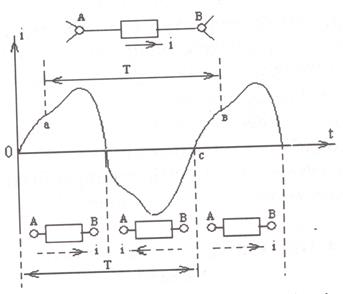
1 – сурет. Айнымалы тоқ графигі

1 – суретте электр тізбегінің АВ бөлігі көрсетілген және периодты ток үшін мысал ретінде токтың уақытқа тәуелділігі келтірілген: і = F(t). Стрелка токтың оң бағытын көрсетеді i›0 i‹0 болған жағдайда токтың нақты бағыттары үзік сызықты стрелкамен көрсетілген.

Қисық сызық бойындағы кесінділер ‹‹а›› мен ‹‹в››, ‹‹0›› және ‹‹с›› аралықтарын токтың бір период кезіндегі толық циклі дейміз.

Периодқа кері шаманы жиілік дейміз, ол ƒ әрпімен белгіленеді және герцпен (Гц) өлшенеді:

ƒ = 1 / T (Гц) (3)

Электротехникада қолданылатын айнымалы токтардың жиілік ауқымы (диапазоны) өте кең. Ол ондаған герцтен миллиард герцке дейін барады. Еуропа электр энергетикасында стандарт жиілік тағайындалған (өндірістік 50 Гц, ал АҚШ пен Жапонияда 60 Гц). Байланыс техникасында жиілігі жоғары (100кГц-тен 30 ГГц-ке дейін) айнымалы тоқ пайдаланылады.

Жоғарыда сөз болған және жаңадан енгізілген анықтамалардың барлығы бұдан былай да кернеу, ЭҚК, магнит ағындары үшін пайдаланыла береді. Кернеу және ЭҚК жайында сөз еткенде, сұлбада олардың оң бағытын стрелкамен немесе әріптің төмен жағына қойылған индекс арқылы белгілеу керек.

Электр энергетикасында қарапайым гармоникалық немесе синусоидалық токтар пайдаланылады, яғни токтың уақытқа тәуелділігі синусоидалық функция болады. Радиотехникада, автоматикада, телемеханикада және есептеу техникасында синусоидалы емес периодты токтарды пайдаланған кезде біраз қиындықтарға кездесеміз. Олар: электр энергиясы шығынының ұлғаюы, тізбектің кейбір бөліктерінде кернеудің едәуір пайда болуы, электр байланыстарының (телеграф, телефон) жұмысатарына кедергі келтіретін бұрмалаушы жағдайлардың тууы.

Синусоидалық емес периодты токтар дегеніміз - әртүрлі жиіліктегі синусоидалық тоқтардың жиынтығы.

Электр тізбектерінің осы құбылыстары бізден синусоидалық токтарды түбегейлі зерттеп - білуді талап етеді.

Тұрақты және айнымалы тоқтың графиктік кескіні(уақытша диаграммалар)

Графиктік әдіс уақытқа тәуелді айнымалы шамалардың өзгеру процесін көрнекті көрсетуге мүмкіндік береді.

2-суретте тұрақты тоқ графигі көрсетілген. Тоқ оң мәндерге ие болады. 3-суретте айнымалы тоқтың графигі бейнеленген. О осі төмен нүктелер теріс мәндерге ие болады.

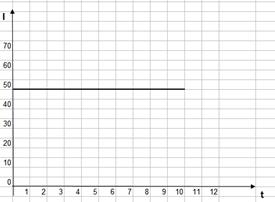
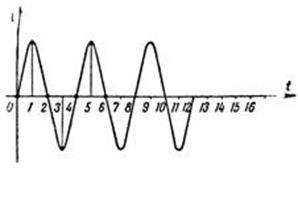
Сурет – 2. Тұрақты тоқ

Сурет – 3. Айнымалы тоқ

2-Суретте тұрақты тоқтың шамасы 50 мА. Бағыты және шамасы бойынша уақыт өткен сайын тоқ шамасы 50 мА болып қала береді.

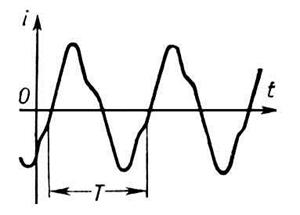
Айнымалы тоқтың периодтық i(t) графигі

Өндірілуі

Айнымалы тоқ айнымалы кернеу арқылы өндіріледі. Тоқ жүріп тұрған сым төңірегінде пайда болатын айнымалы электрлі магниттік өріс айнымалы тоқ тізбегінде энергия тербелісін тудырады, яғни энергия магнит немесе электр өрісінде периодты түрде бірде жиналып, бірде электр энергиясы көзіне қайтып отырады. Энергияның тербелуі айнымалы тоқ тізбектерінде реактивті тоқ тудырады, ол сым мен тоқ көзіне артық ауырлық түсіреді және қосымша энергия шығынын жасайды. Бұл – айнымалы тоқ энергиясын берудегі кемшілік. Айнымалы тоқ күші сипаттамасының негізіне айнымалы тоқтың орташа жылулық әсерін, осындай тоқ күші бар тұрақты тоқтың жылулық әсерімен салыстыру алынған. Айнымалы тоқ күшінің осындай жолмен алынған мәні әсерлік мән деп аталады әрі ол период ішіндегі тоқ күші мәнінің математикалық орташа квадратын көрсетеді. Айнымалы тоқтың әсерлік кернеу мәні де осы сияқты анықталады. Тоқ күші мен кернеудің осындай әсерлік мәндері айнымалы тоқтың амперметр және вольтметрі арқылы өлшенеді.

Таралуы, түрленуі

Айнымалы тоқтың үш фазалық жүйесі жиі қолданылады. Тұрақты тоққа қарағанда айнымалы тоқтың генераторлары мен қозғалтқыштарының құрылымы қарапайым. Айнымалы тоқ әуелі шала өткізгіштер арқылы, ал одан кейін шала өткізгішті инверторлар көмегімен жиілігі реттелмелі басқа айнымалы тоққа түрлендіріледі.

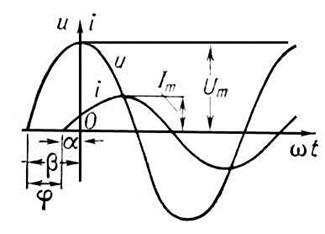
Айнымалы тоқ күшінің лездік мәні (i) синусойдалық заңға сәйкес белгілі бір уақыт (t) ішінде мынадай заң бойынша өзгереді:

i(t)=I_msin(wt+a), мұндағы I_m-тоқ амплитудасы, ω = 2πf – тоқтың бұрыштық жиілігі, a - бастапқы фаза.

Сондай жиіліктегі кернеу де синусойдалық заң бойынша өзгереді:

u(t)=U_msin(wt+b), мұндағы U_m- кернеу амплитудасы, b - бастапқы фаза.

Мұндай айнымалы тоқтың әсерлік мәндері мынаған тең болады:

I = I_m/ 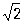» 0,707 I_m, U = U_m/ 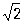» 0,707 U_m.

Айнымалы тоқ тізбегінде индуктивтілік не сыйымдылықтың болуына байланысты тоқ күші (i) мен кернеу (u) арасында y=b-a фаза ығысуы пайда болады.

Айнымалы тоқтың параметрлері

1.Лездік мәні – белгілі уақытқа сәйкес келетін тоқтың шамасы

2. Амплитуда– максимал лездік мәні (айнымалы тоқ жететін мәні).

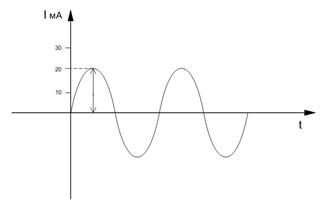
Мұнда амплитуда 20 мА

3. Период - айнымалы тоқ өзгерісінің толық тербеліс жасауға кеткен уақыт Т - әрпімен белгіленеді

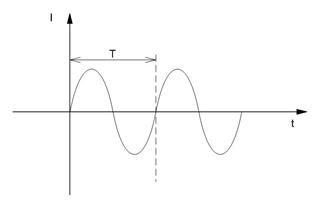
Айнымалы тоқта бір периодта бір тербеліс жасалады, яғни период толық бір тербеліс жасауға кеткен уақыт. Бір тербеліс тоқтың екі қозғалысынан тұрады.

4. Жиілік– айнымалы тоқтың бір секундтағы тербеліс саны

Жоғары жиілігі f әрпімен белгіленеді.Дыбыстық жиілігі F әрпімен белгіленеді.Жиіліктің өлшем бірлігі герц болып табылады, шартты белгісіГц. Егер тоқ секундына бір тербеліс жасаса, онда жиілігі 1Гц-ке тең.

Практикада жиіліктің қысқаша өлшем бірліктері қолданылады - килогерц и мегагерц

1 кГц=1*10³Гц; 1мГц= 1*10⁶ Гц

Анықтама бойынша период пен жиілік бір-біріне қарама қарсы шамалар, яғни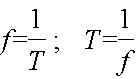

4. Фаза –тербелістің берілген амплитудасы кезінде тербелмелі жүйенің кез келген уақыт мезетіндегі күйін анықтайды.

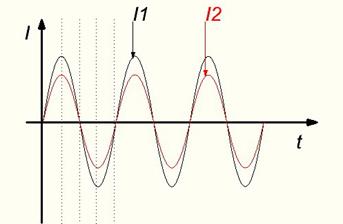
Айнымалы шамалар фаза бойынша сәйкес келуі мүмкін.

Мұнда тоқтар I1 және I2 фаза бойынша сәйкес келеді

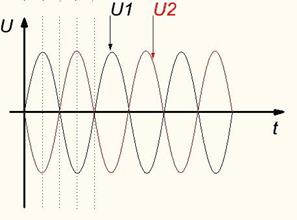
Мұнда кернеу U1 және U2 қарсы фазада болады.

Фаза бойынша жылжуды градуспен көрсетеді. Барлық период 360⁰, себебі период шеңбер бойынша магнит өрісінде өткізгіштің бір толық айланысын алады.

Бұл яғни олар біруақытта нөлдік және максимал мәндеріне қарама-қарсы бағытта жетеді.

Егер айнымалы шамалар фаза бойынша сәйкес келмесе, онда фаза бойынша жылжытылған.

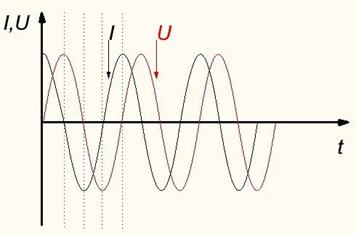
Мұнда кернеу тоқтан 90⁰ –қа қалса, онда тоқ және кернеу фаза бойынша 90⁰ –қа жылжытылған.

Басында тоқ максимумға жетті, ал кернеу нөлде тұр.

Кернеу максимумға 90⁰ –тан кейін жетеді.

Фаза бойынша жылжу грек әрпімен φ белгіленеді, мысалы φ=90⁰ .

Айнымалы тоқ генераторының роторы неғұрлым тез айналса, соғұрлым ЭҚК немесе тоқтың өзгеру периоды аз болады.

Айнымалы тоқтың максималды мәні (ЭҚК немесе кернеу) оның амплитудасы немесе тоқтың амплитудалық мәні деп аталады.

Im, Em және Um — тоқтың, ЭҚК-тің және кернеудің амплитудалары.

i = I_m sin(wt+y_i);

e = E_msin(wt+y_e);

u = U_m sin(wt+y_u);

Өндірістік жиілікті айнымалы тоқтың энергия көзі ретінде электр машиналы генераторлар пайдаланылады, оған айналмалы қозғалыс беретін бірінші қозғалтқыштар: бу машиналары, гидравликалық турбиналар және т.б. қозғалтқыштар жатады. Генератордың айналмайтын бөлігі статордан және айналатын бөлігі ротордан тұрады. Көпшілік жағдайда роторда электромагнит орналасады. Ротор орамдары щеткалар мен сақиналар арқылы тұрақты тоқ көзінен қоректенеді. Ротор айналған кезде осы магниттік ағын статордың өткізгіштерін қиып өтеді, яғни оларда ЭҚК пайда болады.

Е= Blu мұндағы В – саңылаудағы магниттік индукция, l - өткізгіштіктің актив ұзындығы, u – магниттік өрістің өткізгішке қатысты орын ауыстыру жылдамдығы;

800-ден 8000 Гц дейінгі жиіліктер, бұдан да жоғары жиіліктегі айнымалы тоқты тек электрондық генераторлардан алады.

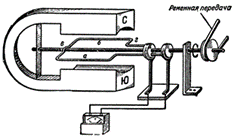
Айнымалы тоқ генераторының қарапайым схемасы

Мұндай құрылғы айнымалы ЭҚК – тің көзі болып табылады.

Айнымалы ЭҚК графигінің құрылымы

Лекция №8. Бір фазалы синусойдалы тоқ. Синусоидалы айнымалы ток тізбегі. Негізгі анықтамалар. Синусоидалы шамалардың әсерлі мәндері. Векторлы диаграмма әдісі.

6.1. Синусоидалы айнымалы ток тізбегі. Негізгі анықтамалар

Техникада қоректендіру көзі ретінде электр энергиясын машинамен және машинасыз түрлендіру қолданылады. Тұрақты тоқ генераторына қарағанда айнымалы тоқ генераторын жасау өте қарапайым, сенімдірек және арзан. Оларда тұрақты реттеуді қажет ететін және арнайы қызмет көрсетуді қажет ететін коллектор жоқ. Көбіне өте қарапайым және сенімді айнымалы тоқ қозғалытқыштары, әсіресе асинхронды двигательдер пайдаланылады.

Ұшатын аппарат бортында синусоидалы айнымалы токты электр тізбегін қолдану құралдар мен агрегаттар (тартпаларының) жетектерінің айналу жиілігін тұрақтандыруды қамтамасыз етеді. Жоғары жиіліктегі электр тоғын қолдана отырып, өте үлкен айналу жиілігін алуға және массасы мен электр құрылғының негізгі элементтерінің шектік көлемін анағұрлым жеңілдетуге азайтуға болады. Айнымалы тоқ тізбегінің тағы бір артықшылығы оны трансформаторлауға (мүлдем өзгертуге немесе ауыстыруға) мүмкіншілік бар.

Синусоидалы шамалардың лездік мәндері мына формулалармен анықталады:

,

,

,

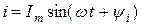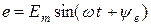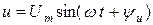мұндағы 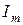, , 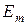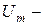тоқтың, ЭҚК-тің және кернеудің амплитудалары;

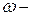бұрыштық жиілік;

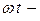фазалық бұрыш;

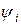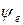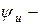, , тоқтың, ЭҚК-тің және кернеудің алғашқы фазалары.

Сызықтық жиілік бұрыштық жиілікпен және периодпен мына қатынастармен байланысқан , .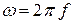

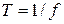6.2. Синусоидалы шамалардың әсерлі мәндері

Синусоидалы тоқтың жылулық және электродинамикалық іс-әрекетін сипаттау үшін синусоидалы тоқтың әсерлі мәндері деген түсінік енгізіледі.

Синусоидалы тоқтың әсерлі мәні айнымалы жылулық немесе механикалық іс-әрекетке эквивалентті өндірілетін тұрақты тоқтың мәні болып табылады.

Бір период уақыт аралығында тұрақты тоқтың жылулық әсері

.

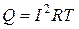Осы уақыт аралығында сол кедергідегі айнымалы тоқтың әсерлі шамасы сондай жылу мөлшерін өндіреді, яғни

.

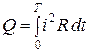Бұл жағдайда айнымалы тоқтың әсерлі мәнін мына қатынастан анықтауға болады

,

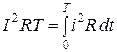яғни .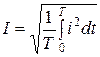

Синусоидалы шаманың әсерлі мәні бір периодтағы осы шаманың орташа квадраттық мәні болып табылады. Егер тоқ синусоидамен өзгеретін болса, яғни 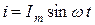, онда

.

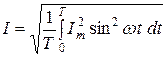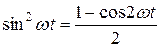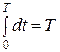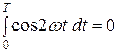, , екенін ескере отырып,

.

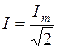Синусоидалы шаманың әсерлі мәні оның амплитудалық мәнінен 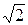есе кіші

, , .

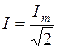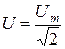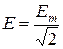Кирхгофтың бірінші және екінші заңдары тоқ пен ЭҚК-тің лездік мәндері үшін де дұрыс, яғни

, .

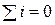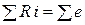6.3. Векторлық диаграмма әдісі

Векторлық диаграмма әдісі синусоидалы шамалардың алгебралық қосындыларын векторлық анализ ережесіне сәйкес векторлармен геометриялық іс-әрекетпен алмастыруға мүмкіндік береді.

Векторлық диаграмма әдісінің мәнісі мынада:

· әрбір синусоидалы шамаға осы шаманың векторы сәйкес келеді;

· синусоидалы шама векторының бағыты алғашқы фазамен анықталады;

· синусоидалы шама векторының модулі әсерлі мәнге немесе осы шаманың амплитудасына пропорционал;

· бірдей бұрыштық жиіліктегі синусоидалы шама векторын кәдімгі векторды геометриялы түрде қосуға болады

Бұрыштың оң бағыты сағат тілінің жүрісіне қарама-қарсы есептеледі.

Сонымен, егер 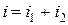тоқты анықтау қажет болса, онда Кирхгофтың І – заңына сәйкес (6.1 – сурет) мынадай алгебралық әрекет жүргіземіз:

,

,

.

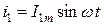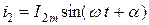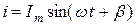Тоқтың алғашқы фазасы мен амплитудасын анықтау өте қиын. Векторлық диаграмма әдісіне сәйкес бұл тоқты міндетті түрде масштабпен құрылатын векторлық диаграмма (6.2 – сурет) көмегімен анықтау тіпті оңай.

6.1 – сурет 6.2 – сурет

6.4. Символдық әдіс

Синусоидалы тоқ тізбегін есептеу үшін символдық әдіс те қолданылады.

Символдық әдіс вектормен жүргізілетін геометриялық іс-әрекетті алгебралыққа ауыстыруға мүмкіндік береді. Сондай-ақ айнымалы тоқ тізбегін есептеуді тұрақты тоқ тізбегін есептейтін әдіспен жүргіземіз.

Символдық әдіс былай жүргізіледі:

а) әрбір 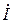вектор тік бұрыш координат жүйесі өсінд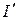е және 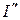құраушыларға жіктеледі (6.3 –сурет);

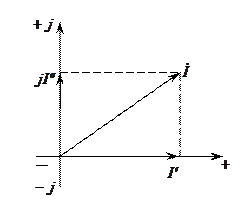
6.3 – сурет

б) абсцисса өсін нақты мәндер өсі деп атайды және «+», «–» таңбаларымен белгіленеді. Ордината өсін жорамал мәндер өсі деп атайды. Жорамал өстегі вектор құраушысын 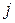ерекше символымен белгілейді. Сондықтан бұл әдіс символдық деп аталады. 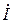векторы мынаған тең:

;

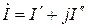в) әрбір векторды 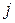символына көбейту осы векторды сағат тілінің жүрісіне қарама-қарсы 90⁰ – қа бұрады. 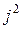- қа көбейту векторды 180⁰ – қа бұрады, яғни 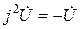, осыдан 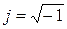. 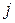символы - бұл жорамал бірлік;

г) вектор комплексті шама сияқты комплексті жазықтықта қарастырылады. Сондықтан бұл әдісті «комплексті шамалар әдісі» деп те атайды.

6.5. Айнымалы тоқтың комплексті түрде жазылуы.

Комплексті түрдегі әсерлі мәндер үстіне нүкте қойылған негізгі әріптік белгілеу арқылы жазылады. Комплексті шамаларды жазудың үш түрі қолданылады:

а) алгебралық түрі ;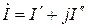

б) тригонометриялық түрі ;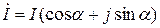

в) көрсеткіштік түрі .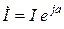

Соңғысы Эйлер формуласынан шығады .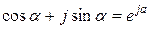

Бір түрден екіншісіне өту үшін мына қатынастар қолданылады

, ,

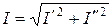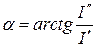мұндағы 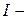комплекс модулі; 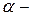алғашқы фаза.

Лекция №9. Бірфазалы синусойдалы тоқ тізбегін есептеу әдістері. Бір фазалы айнымалы тоқ. Активті, индуктивті және сыйымдылықты кедергілері бар айнымалы тоқ тізбегі

7.1. Активті кедергісі бар айнымалы тоқ тізбегі

Егер 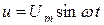синусоидалы кернеуге резисторлы элемент қоссақ (7.1 – сурет), онда тізбекте лездік тоқ пайда болады:

.

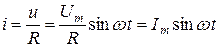Сонымен мынадай қорытынды жасауға болады: синусоидалы кернеуге қосылған активті кедергісі бар тізбектегі тоқ синусоидалы болып табылады және кернеумен фаза бойынша сәйкес келеді.

Мұндай тізбектің векторлы диаграммасы 7.2 – суретте кескінделген.

Тоқ векторы кернеу векторымен бағыты бойынша сәйкес келеді (фаза бойынша ығысу нөлге тең).

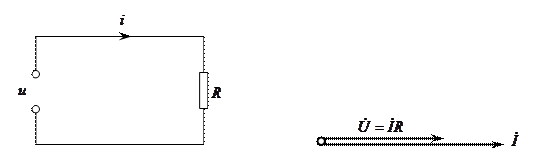
7.1 – сурет 7.2 – сурет

Мұндай тізбек үшін Ом заңының амплитудалық мәнінің, әсерлі мәнінің және комплексті түрдегі жазылулары төмендегідей

, , .

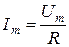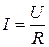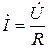Өткізгіштің бетіне тоқты ығыстырып шығару құбылысымен байланысқан айнымалы тоқ өткізгіштерінің өсуін ескеру қажет. Беттік эффект

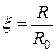
коэффициентін енгізу арқылы ескеріледі, мұндағы

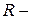тұрақты тоққа қосылған өткізгіштің кедергісі,

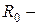айнымалы тоққа қосылған осы өткізгіштің кедергісі.

7.2. Индуктивті кедергісі бар айнымалы тоқ тізбегі

Егер индуктивті элементі бар тізбекте 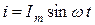синусоидалы тоқ өтетін болса, онда өздік индукцияның ЭҚК-і

.

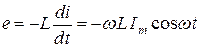Кирхгофтың ІІ-заңы бойынша

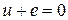
кернеуді мына қатынаспен жазуға болады

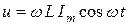
немесе ,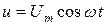

мұндағы .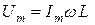

Сонымен синусоидалы кернеуге қосылған индуктивті кедергісі бар тізбектегі тоқ синусоидалы болады және ол кернеуден периодтың төрттен біріне артта қалады.

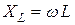шамасының өлшем бірлігі кедергінікіндей және индуктивті кедергі деп аталады. Индуктивті кедергі активтіден өзгеше болады және реактивті кедергі деп аталады. Комплексті индуктивті кедергі мына қатынаспен анықталады

.

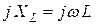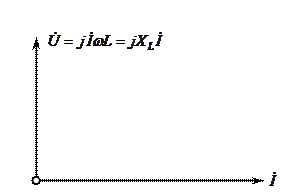Бұл тізбектің векторлық диаграммасы 7–3 суретте келтірілген. Кернеу векторы тоқ векторынан 90⁰ – қа озып кетеді ( 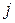символы тоқ векторын периодтың төрттен біріне сағат тіліне қарама-қарсы бұру қажет екенін көрсетеді).

Индуктивті элементі бар тізбек үшін Ом заңының амплитудалық мәнінің, әсерлі мәнінің және комплексті түрдегі жазылулары төмендегідей

, , .

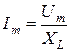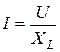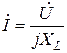7–3 сурет

7.3. Сыйымдылықты кедергісі бар айнымалы тоқ тізбегі

Егер синусоидалы тоқ тізбегінде идеаль сыйымдылықты элемент болса, онда тоқ мына заңмен өзгереді

.

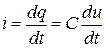Егер 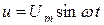, онда 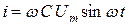немесе ,

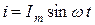мұндағы .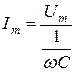

Сыйымдылықты синусоидалы кернеуге қосқан кезде синусоидалы тоқ тұрақталады және ол кернеуден периодтың төрттен біріне озып кетеді.

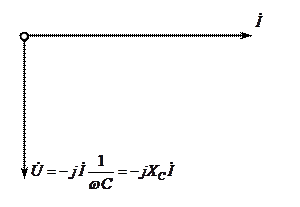
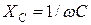шамасының өлшем бірлігі кедергінікіндей және сыйымдылықты кедергі деп аталады. Сыйымдылықты кедергі индуктивті кедергі сияқты реактивті кедергі болып табылады. Индуктивті кедергі тоқ пен индуктивті элементтің жиілігінің жоғарылауымен бірге өседі. Тұрақты тоқ тізбегіндегі индуктивтілікте реактивті кедергі болмайды. Тұрақты тоқтағы 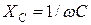сыйымдылықты кедергі шексіздікке тең және айнымалы тоқ пен сыйымдылық элемент жиілігінің жоғарылауымен кемиді.

Тізбектің векторлық диаграммасы 7–4 суретте келтірілген. Тоқ векторының 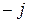- ға көбейтіндісі осы вектордың 90⁰ – қа сағат тілінің бағытымен бұрылуын көрсетеді.

7–4 сурет

Сыйымдылықты элементі бар тізбек үшін Ом заңының амплитудалық мәнінің, әсерлі мәнінің және комплексті түрдегі жазылулары төмендегідей

, , .

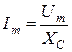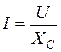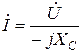Лекция №10. Көпфазалы айнымалы тоқ тізбегі. Айнымалы тоқтың тармақталмаған және тармақталған тізбектері. Кедергілер мен өткізгіштіктер ұшбұрышы. Кедергілер мен өткізгіштіктер арасындағы қатынастар.

8.1. Айнымалы тоқтың тармақталмаған тізбектері

Элементтерді тізбектей қосқан кезде (8–1 сурет) кернеудің лездік және комплексті мәндері мына қатынастармен жазылады

,

.

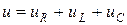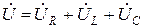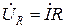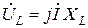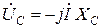, , болғандықтан векторлық диаграмма 8–2 суретте көрсетілген түрдегідей болады.

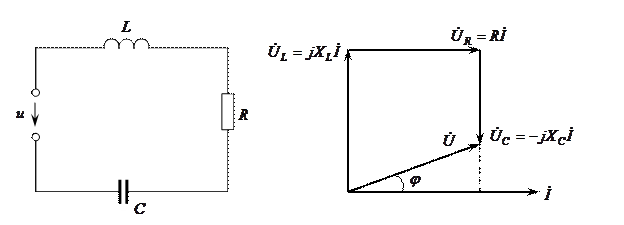
8–1 сурет 8–2 сурет

Векторлық диаграммадан кернеу комплексінің өрнегін жазуға болады

,

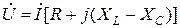немесе .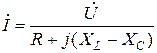

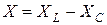айырымы реактивті кедергі деп аталады, оның комплексті түрі .

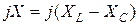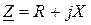немесе 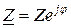немесе 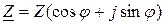өрнектерін комплексті түрдегі толық кедергі деп атайды. Толық кедергінің модулін былай өрнектеуге болады

,

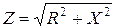ал тоқ пен кернеу арасындағы бұрыш – 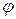мына қатынастан анықталады

.

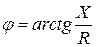Тікбұрышты үшбұрышты векторлық диаграммада кедергілер үшбұрышына түрлендіруге болады (8–3 сурет). Кедергілер үшбұрышынан мынадай қатынастар шығады:

,

,

,

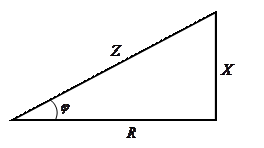
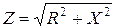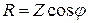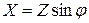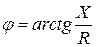немесе .

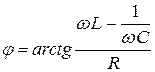8–3 сурет

Фазалық ығысу оң деп есептеледі, егер .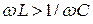

Тармақталмаған тізбек үшін Ом заңы үшін әсерлі мәндері және комплексті түрдегі жазылуы

, ,

, .

, .

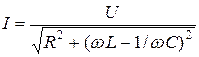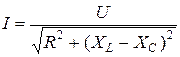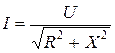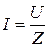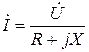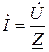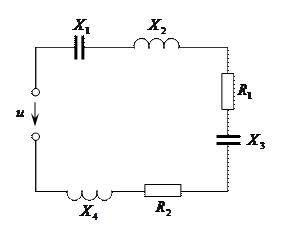
Тармақталмаған тізбекті символдық әдіспен есептеуді тұрақты тоқтың тізбегі сияқты есептеуге болады. 8–4 суреттегі тізбекті есептеу үшін толық кедергіні анықтау қажет, яғни мына қатынасты жазуға болады

.

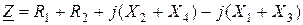Сонымен барлық индуктивті кедергі « 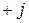» символына көбейтіледі, ал барлық сыйымдылықты кедергі « 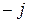» символына көбейтіледі. Егер , , , , , ,

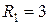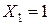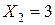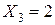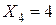онда

.

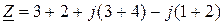
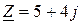8–4 сурет

Осыдан шығатын қорытынды барлық тізбекті эквивалентті кедергімен ауыстыруға болады. Бұл кедергі нақты (активті кедергі 5 Ом) және жорамал (индуктивті реактивті кедергі 4 Ом) бөліктерден тұрады.

8.2. Айнымалы тоқтың тармақталған тізбектері

Элементтерді параллель қосқан кезде (8–5 сурет) тоқтың лездік мәні мен комплексті түрі Кирхгофтың І–заңы бойынша мына қатынастармен жазылады

,

.

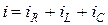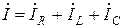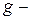активті, 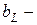реактивті индуктивтілік, 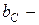реактивті сыйымдылық өткізгіштік арқылы символдық түрі былай жазылады

, , .

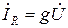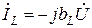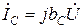Кирхгофтың І–заңына сәйкес векторлық диаграммасы 8–6 суреттегідей болады.

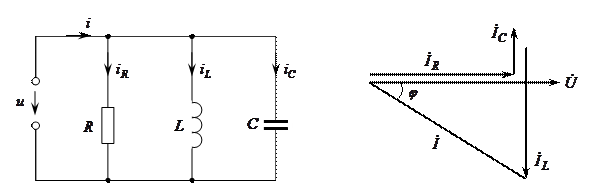
8–5 сурет 8–6 сурет

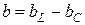айырымын реактивті өткізгіштік деп атайды. Бұл жағдайда толық өткізгіштікті комплесті түрде былай анықтауға болады

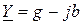немесе 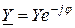немесе 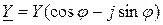, мұндағы толық өткізгіштіктің модулі

,

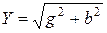ал тоқ пен кернеу арасындағы фазалық ығысу –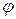

.

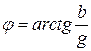Векторлық диаграмманың тікбұрышты үшбұрышын өткізгіштіктер үшбұрышына түрлендіруге болады (8–7 сурет). Осы үшбұрыштан өткізгіштіктер арасындағы мынадай қатынастар шығады:

,

,

,

.

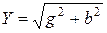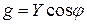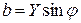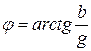8–7 сурет

Векторлық диаграмманың тікбұрышты үшбұрышы сондай-ақ мына қатынасты береді

.

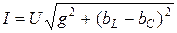Бұл қатынас тармақталған тізбек үшін алгебралық түрдегі Ом заңы болып табылады. Ом заңы символдық түрде былай жазылады

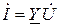немесе .

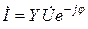8.3. Кедергілер мен өткізгіштіктер ұшбұрышы. Кедергілер мен өткізгіштіктер арасындағы қатынастар

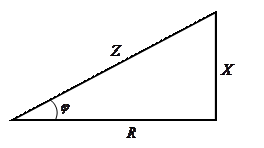
Кедергілер ұшбұрышы мен өткізгіштіктер үшбұрышы векторлық диаграмманы түрлендіру арқылы тұрғызылады (8–8 сурет). Кедергіл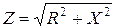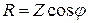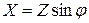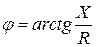ер үшбұрышы үшін мына қатынастар:

,

,

,

,

ал өткізгіштіктер үшбұрышы үшін мына қатынастар:

,

,

,

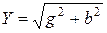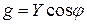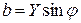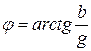орындалады.

8–8 сурет

Бұл үшбұрыштардағы 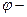бұрышы (тоқ пен кернеу арасындағы фазалық ығысу) бірдей, яғни бұл үшбұрыштар ұқсас. Анықтама бойынша

,

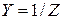сондықтан кедергілер мен өткізгіштіктер арасындағы мынадай қатынастарды құруға болады

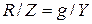және т.б.

Кедергі арқылы өрнектелген өткізгіштік мына түрде болады:

,

,

.

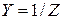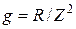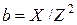Өткізгіштік арқылы өрнектелген кедергі мына түрде болады:

,

,

.

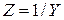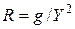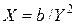Символдық түрдегі қатынастар мына түрде болады

,

.

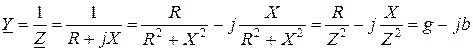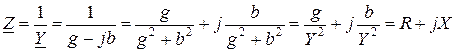Толық кедергіні электр тізбегінің импедансы деп атайды. Активті кедергіні резистанс, реактивтіні – реактанс деп атайды. Реактанс индуктивті (индуктивті кедергі) және (сыйымдылықты кедергі) сыйымдылықты болады. Толық өткізгіштікті электр тізбегінің адмитансы деп атайды. Активті өткізгіштікті кондуктанс, реактивтіні – сусцептанс деп атайды. Сусцептанс индуктивті (индуктивті өткізгіштік) және (сыйымдылықты өткізгіштік) сыйымдылықты болады.

Лекция № 11. Үшфазалы синусойдалы тоқ тізбегін есептеу әдістері. Айнымалы тоқ тізбегінің қуаты. Қуаттар балансы. Қуат коэффициенті. Қуат коэффициентінің жоғарылауы

9.1. Айнымалы тоқ тізбегінің қуаты

Айнымалы тоқ тізбегінің лездік қуаты лездік тоқ пен лездік кернеудің көбейтіндісі ретінде анықталады

.

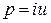Қуаттың символдық түрі кернеу комплексі мен тоқ комплексінің сыңарласына көбейтіндісі ретінде анықталады, яғни

.

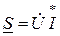Егер , , ,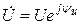

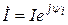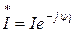онда 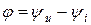(фазалық ығысу),

ал .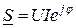

Бұл өрнек толық қуаттың көрсеткіштік түрде жазылуы. Қуаттың алгебралық және тригонометриялық түрде жазылуын анықтауға болады

,

,

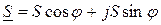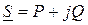мұндағы 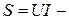толық қуаттың модулі;

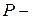активті қуат;

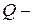реактивті қуат.

Қуаттар үшбұрышы 9–1 суретте келтірілген. Бұл үшбұрыш мына қатынастарды береді

,

,

,

.

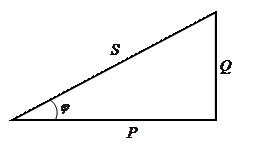
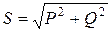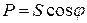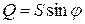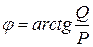9–1 сурет

Сонымен, толық қуат – комплексті шама. Активті қуат толық қуаттың нақты бөлігі, реактивті – толық қуаттың жорамал бөлігі болып табылады. Егер бірнеше электр энергиясын қабылдағыштар болса, онда толық қуат үшін қатынас мына түрде болады

.

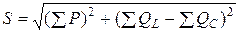Қуаттар балансын мына теңдеумен анықтауға болады

,

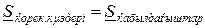мұндағы 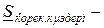барлық қоректендіру көздерінің қуаты,

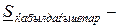тізбектің барлық қабылдағыштарының қуаты,

яғни .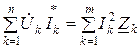

Кернеу мен тоқ көзі қарама-қарсы болған кезде 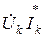көбейтіндісі «–» таңбамен алынатын есте сақтау қажет. Егер тоқ көзі қабылдағыш тәртібімен жұмыс жасаса (тоқ пен кернеу бағыттас), онда 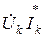көбейтіндісін оң таңбамен алу қажет.

Қоректендіру көзінің ішкі кедергісін электр энергиясының қарапайым қабылдағышы деп есептейді.

9.2. Қуат коэффициенті. Қуат коэффициентінің жоғарылауы

Активті кедергі мына қатынаспен анықталады

.

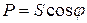Бұл өрнектегі 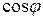қуат коэффициенті деп аталады. Ол электр энергияның қолдану дәрежесін сипаттайды. Сондықтан қуат коэффициентін жоғарылату мәселесі маңызды болып табылады.

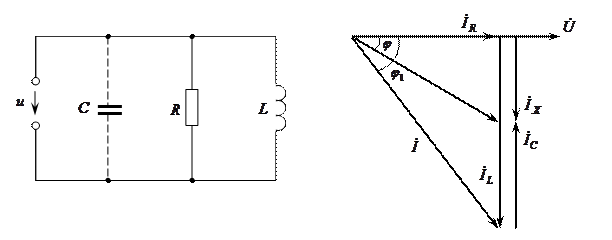
9–2 сурет 9–3 сурет

9–2 суретте ұшатын аппараттың немесе өнеркәсіп өндірісінде энергияны пайдаланудың типтік схемасы кескінделген. Қуатты қабылдағыштардың көпшілігі индуктивтік сипатта.

Мұндай тізбектің векторлық диаграммасы 9–3 суретте келтірілген. Фазалық ығысуды азайту (қуат коэффициентін жоғарылату) үшін қабылдағышқа конденсатор батареяларын параллель қосады. Бұл жағдайда векторлық диаграмма өзгереді, 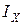реактивті ток, тоқ пен кернеу арасындағы бұрыш азаяды.

Фазалық ығысуды 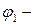ден 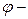ге азайту үшін қажетті қосымша сыйымдылықты анықтауға болады:

,

,

,

,

,

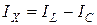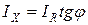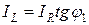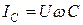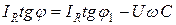осыдан .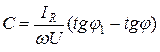

Егер 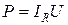тәуелділігін қолдансақ, қосымша сыйымдылықты мына қатынаспен анықтауға болады

.
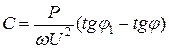