Нормальный закон распределения. Закон равномерной плотности
Плотность вероятности нормально распределенной случайной величины имеет вид:
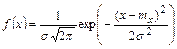 , где
, где 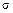 - среднее квадратичное отклонение,
- среднее квадратичное отклонение, 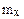 - математическое ожидание. Вероятность попадания нормально распределенной случайной величины Х в интервал
- математическое ожидание. Вероятность попадания нормально распределенной случайной величины Х в интервал 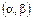 вычисляется по формуле:
вычисляется по формуле:
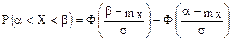 , где
, где
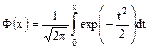 - функция Лапласа (интеграл вероятности).
- функция Лапласа (интеграл вероятности).
Вероятность того, что абсолютная величина отклонения меньше положительного числа 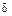 :
: 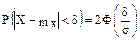
Равномерным называют распределение вероятностей непрерывной случайной величины Х, если на интервале (а, b), которому принадлежат все возможные значения Х, дифференциальная функция сохраняет постоянное значение, а именно 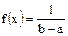 , вне этого интервала
, вне этого интервала 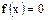 .Для равномерно распределенной случайной величины
.Для равномерно распределенной случайной величины 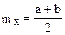
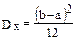
6.1 Случайная величина Х распределена нормально с 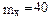 ,
, 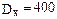 . Записать плотность распределения вероятностей Х. Вычислить
. Записать плотность распределения вероятностей Х. Вычислить
вероятность попадания случайной величины Х в интервал (30, 80).
Решение:
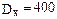 , следовательно
, следовательно 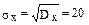
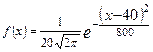
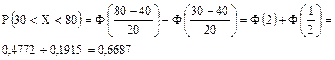
6.2 Вывести правила “ 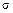 ”, “двух
”, “двух 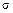 ” и “трех сигм”: вероятность того, что абсолютная величина отклонения нормально распределенной случайной величины будет: а) меньше
” и “трех сигм”: вероятность того, что абсолютная величина отклонения нормально распределенной случайной величины будет: а) меньше 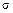 , равна 0,6826; б) меньше 2
, равна 0,6826; б) меньше 2 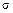 , равна 0,9544; в) меньше утроенного среднего квадратичного отклонения, равна 0,9973.
, равна 0,9544; в) меньше утроенного среднего квадратичного отклонения, равна 0,9973.
Решение:
а) 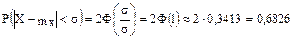
( 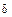 в данном случае равняется
в данном случае равняется 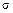 )
)
б) 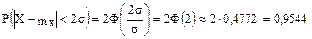
в) 
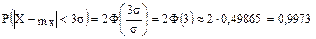
6.3 Случайная величина Х распределена нормально с 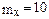 ,
, 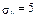 . Найти интервал, в который с вероятностью 0,9973 попадет в результате испытания величина Х.
. Найти интервал, в который с вероятностью 0,9973 попадет в результате испытания величина Х.
Решение:
По правилу “трех сигм” случайная величина Х с вероятностью 0,9973 попадет в интервал ( 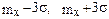 ), который в данном случае
), который в данном случае
( 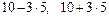 )=(-5, 25)
)=(-5, 25)
6.4 На некоторый полезный сигнал накладывается нормально распределенная помеха X с плотностью распределения 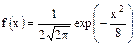 , где X – напряжение тока в В. Найти вероятность того, что помеха по абсолютной величине не превысит: а) 4В; б) 6В.
, где X – напряжение тока в В. Найти вероятность того, что помеха по абсолютной величине не превысит: а) 4В; б) 6В.
Решение:
Из формулы для плотности вероятностей X, следует, что m=0, 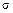 =2.
=2.
а) 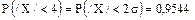 (4=2
(4=2 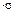 ) по правилу “двух сигм”.
) по правилу “двух сигм”.
б) 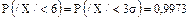 (6=3
(6=3 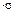 ) по правилу “трех сигм”.
) по правилу “трех сигм”.
6.5 Для замера напряжений используются специальные датчики. Определить среднюю квадратическую ошибку датчика, если он не имеет систематических ошибок, а случайные распределены по нормальному закону и с вероятностью 0,8 не выходят за пределы ±0,2 мкв.
Решение:
Случайная величина Х – ошибка датчика 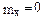 , т.к. датчик не имеет систематических ошибок. По условию
, т.к. датчик не имеет систематических ошибок. По условию 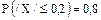

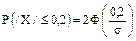 , следовательно
, следовательно
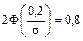
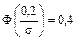 , по таблице для функции
, по таблице для функции 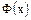
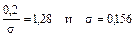 .
.
6.6 Коробки с шоколадом укладываются автоматически, их
средняя масса равна 1,06 кг. Найти стандартное отклонение, если 2,5% коробок имеют массу меньше 1 кг.
Предполагается, что масса коробок распределена по нормальному закону.
Решение:
Случайная величина Х – масса коробки. Т.к. средняя масса коробки равна 1,06, то 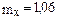 . 2,5% коробок имеют массу меньше 1 кг, т.е.
. 2,5% коробок имеют массу меньше 1 кг, т.е.
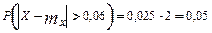
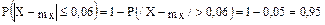
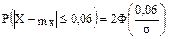 , отсюда
, отсюда 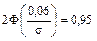
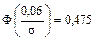 ,
, 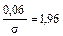 (по таблице функции Лапласа)
(по таблице функции Лапласа)
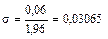
6.7 Автомат штампует детали. Контролируется длина детали Х, которая распределена нормально. Проектная длина равна 50 мм. Фактически длина изготовленных деталей не менее 32 мм и не более 68 мм. Найти вероятность того, что длина наудачу взятой детали: а) больше 55 мм, б) меньше 40 мм. Записать плотность распределения этой случайной величины.
Решение:
Случайная величина Х – длина детали. Так как проектная длина равна 50 мм, то 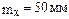 . Требуется найти вероятность того, что длина наудачу выбранной детали меньше 40 мм, но поскольку истинная длина заключена в интервале от 32 до 68 мм, то нужно найти вероятность того, что 32<X<40. Нахождение вероятности Х>55 сводится к вероятности того, что 55<X<68.
. Требуется найти вероятность того, что длина наудачу выбранной детали меньше 40 мм, но поскольку истинная длина заключена в интервале от 32 до 68 мм, то нужно найти вероятность того, что 32<X<40. Нахождение вероятности Х>55 сводится к вероятности того, что 55<X<68.
Итак, следует применить формулу
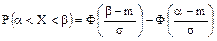
Неизвестным считается среднее квадратическое отклонение 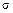 . Из условия задачи известно, что
. Из условия задачи известно, что 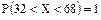 , т.к. фактическая длина деталей лежит в интервале (32, 68).
, т.к. фактическая длина деталей лежит в интервале (32, 68).
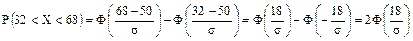 в силу нечетности функции Лапласа. Итак,
в силу нечетности функции Лапласа. Итак, 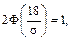
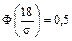 откуда
откуда 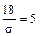 , а
, а  =3,6. Следовательно, плотность распределения случайной величины Х
=3,6. Следовательно, плотность распределения случайной величины Х
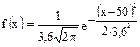 , а искомые вероятности
, а искомые вероятности
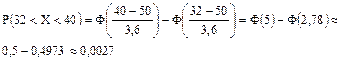
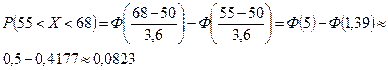
6.8 Браковка шариков для шарикоподшипников производится следующим образом: если шарик не проходит через отверстие диаметром 
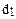 , но проходит через отверстие диаметром
, но проходит через отверстие диаметром 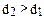 , то его размер считается приемлемым. Если какое-нибудь из этих условий не выполняется, то шарик бракуется. Известно, что диаметр шарика Х – случайная величина, распределенная по нормальному закону с параметрами
, то его размер считается приемлемым. Если какое-нибудь из этих условий не выполняется, то шарик бракуется. Известно, что диаметр шарика Х – случайная величина, распределенная по нормальному закону с параметрами 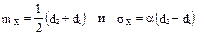 , где
, где 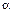 - параметр
- параметр
(0< 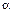 <
< 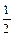 ), который определяет точность изготовления шариков.
), который определяет точность изготовления шариков.
а) Определить вероятность того, что шарик будет забракован. б) Какую точность изготовления следует установить, чтобы брак составлял не более 2% всей продукции?
Решение:
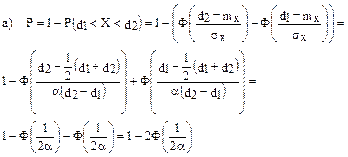
б) 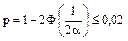 (вероятность брака 2% из 100%)
(вероятность брака 2% из 100%)
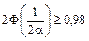 ,
, 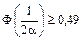 ,
, 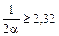
(по таблице функции Лапласа) 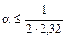 ,
, 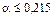
6.9 Высотомер самолета делает систематическую ошибку +20 м. и случайные ошибки, подчиненные нормальному закону со средним квадратичным отклонением 30 м. Для самолета отведен коридор высотой в 100 м. Какова вероятность того, что он будет лететь: а) внутри коридора; б) ниже коридора; в) выше коридора?
Решение:
Пусть случайная величина Х – ошибка высотомера.
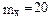 , т.к. систематическая ошибка 20 м.,
, т.к. систематическая ошибка 20 м., 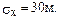 Предполагается, что летчик ведет самолет наиболее разумным способом, т.е. так, чтобы высотомер показывал середину отведенного коридора. Тогда самолет будет лететь внутри коридора, если /Х/<50 м.
Предполагается, что летчик ведет самолет наиболее разумным способом, т.е. так, чтобы высотомер показывал середину отведенного коридора. Тогда самолет будет лететь внутри коридора, если /Х/<50 м.
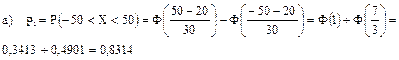
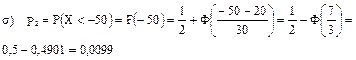
Использовали определение функции распределения 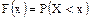 и свойство функции нормального распределения
и свойство функции нормального распределения
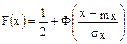
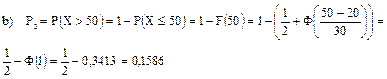
6.10 Составить выражения дифференциальной и интегральной функций распределения фазы 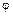 вектора, который с равной вероятностью может иметь любую фазу в интервале (0;2
вектора, который с равной вероятностью может иметь любую фазу в интервале (0;2 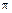 ).
).
Решение: 
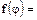

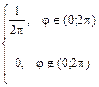
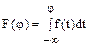
1) 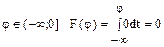
2) 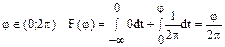
3) 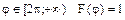
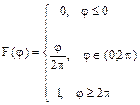
6.11 Цена деления шкалы вольтметра 0,2. Показания прибора округляют до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка: а) больше 0,01; б) меньше 0,06.
Решение:
Ошибку округления можно рассматривать как случайную величину Х, распределенную равномерно между двумя целыми делениями
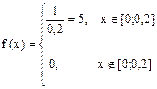
Ошибка отсчета превысит 0,01, если она будет заключена в интервале (0,01;0,19). По формуле 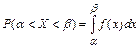 , получим
, получим
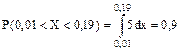
Ошибка будет меньше 0,06, если она будет заключена в интервале (0;0,06) или в интервале (0,14;0,2)
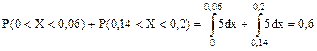
6.12 Поезда метро идут с интервалом 2 минуты. Пассажир выходит на платформу в произвольный момент времени. Определить плотность и интегральную функцию распределения времени ожидания поезда, математическое ожидание, дисперсию и вероятность того, что пассажир будет ожидать очередной поезд меньше 30 секунд.
Решение:
Случайная величина Х – время ожидания, величина распределена равномерно в интервале (0;2)
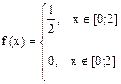
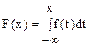
1) 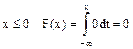
2) 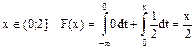
3) 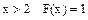
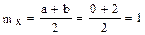 ,
,
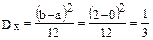
Пассажир будет ожидать очередной поезд меньше 30 сек. (1/2 минуты), если случайная величина Х заключена в интервале (1,5;2)
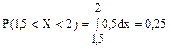
6.13 Рыболов ловит рыбу в пруду, где равновероятно поймать любую рыбу от 0,2 до 1 кг при каждом забрасывании снасти. Найти среднюю величину улова и вероятность поймать при одном забрасывании не более 0,8 кг.
Решение:
Случайная величина Х – величина улова
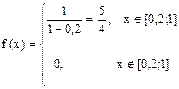
Средняя величина улова 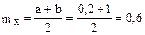
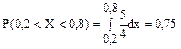
6.14 На перекрестке стоит автоматический светофор, в котором 1 минуту горит зеленый свет и 0,5 минуты – красный, затем опять 1 минуту горит зеленый свет; 0,5 минуты – красный и т.д. Некто подъезжает к перекрестку на машине в случайный момент, не связанный с работой светофора. а) найти вероятность того, что он проедет перекресток, не останавливаясь. б) Найти закон распределения и числовые характеристики времени ожидания у перекрестка.
Решение:
Момент проезда автомашины через перекресток распределен равномерно в интервале, равном периоду смены цветов в светофоре. Этот период равен 1+0,5=1,5 (мин.)
Чтобы машина проехала через перекресток, не останавливаясь, достаточно, чтоб момент проезда перекрестка пришелся на интервал времени (0;1),
т.е. 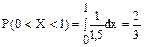
Время ожидания 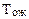 есть смешанная случайная величина, с вероятностью 2/3 она равна 0, а с вероятностью 1/3 принимает с одинаковой плотностью вероятности любое значение между 0 и 0,5 мин. Среднее время ожидания у перекрестка
есть смешанная случайная величина, с вероятностью 2/3 она равна 0, а с вероятностью 1/3 принимает с одинаковой плотностью вероятности любое значение между 0 и 0,5 мин. Среднее время ожидания у перекрестка
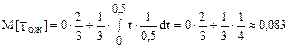 (мин)
(мин)
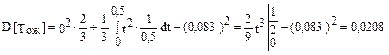 (мин2).
(мин2).
6.15 Случайная величина Х имеет нормальное распределение с параметрами 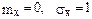 . Что больше
. Что больше 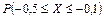 или
или 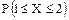 ?
?
Ответ: р1=0,1517; р2=0,1359
6.16 На полезный сигнал накладывается случайная нормально распределенная помеха с плотностью распределения 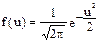 , где u – напряжение в В. Найти вероятность того, что помеха не превысит по абсолютной величине 3В.
, где u – напряжение в В. Найти вероятность того, что помеха не превысит по абсолютной величине 3В.
Ответ: 0,9973
6.17 Производится взвешивание некоторого вещества без систематических ошибок. Случайные ошибки взвешивания подчинены нормальному закону со средним квадратическим отклонением 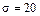 .
.
Найти вероятность того, что взвешивание будет произведено с ошибкой, не превосходящей по абсолютной величине 10 г.
Ответ: 2Ф(0,5)=0,383
6.18 На станке изготавливается некоторая деталь. Ее длина представляет собой случайную величину, распределенную по нормальному закону со средним значением 20 см и дисперсией 0,04 см 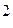 . Найти вероятность того, что длина детали будет заключена между 19,7 см и 20,3 см. Какую точность длины изделия можно гарантировать с вероятностью 0,95.
. Найти вероятность того, что длина детали будет заключена между 19,7 см и 20,3 см. Какую точность длины изделия можно гарантировать с вероятностью 0,95.
Ответ: р1=Ф(1,5)=0,8664 (5 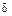
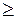 1,96)
1,96) 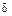
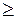 0,392
0,392
6.19 Стрельба ведется из точки О вдоль прямой ОХ. Средняя дальность полета снаряда равна 1200 м. Предполагая, что дальность полета Н распределена по нормальному закону со средним квадратическим отклонением 40 м, найти, какой процент выпускаемых снарядов даст перелет от 60 до 80 м.
Ответ: P(1260<X<1280)=0,0444% (Ф(2)=0,4772 Ф(1,5)=0,4332)
6.20 Цена деления шкалы измерительного прибора 0,2. Показания прибора округляют до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка: а) меньшая 0,04; б) большая 0,05.
Ответ: р1=0,4; р2=0,5
6.21 Автобусы некоторого маршрута идут строго по расписанию. Интервал движения 5 минут. Найти вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобус меньше 3 минут.
Ответ: р=0,6.
§7.Системы случайных величин.
Двумерной называют случайную величину (X,Y), возможные значения которой есть пары чисел 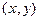 . Составляющие X и Y,рассматриваемые одновременно, образуют систему двух случайных величин.
. Составляющие X и Y,рассматриваемые одновременно, образуют систему двух случайных величин.
Дискретной называют двумерную случайную величину, составляющие которой дискретны. Непрерывной называют двумерную случайную величину, составляющие которой непрерывны. Интегральной функцией распределения двумерной случайной величины называют 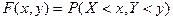 .
.
Закон распределения дискретной случайной величины может быть задан:
а)в виде таблицы с двойным входом,содержащей возможные значения и их вероятности; б)аналитически,например,в виде интегральной функции.
Дифференциальной функцией распределения непрерывной двумерной случайной величины называют 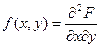
Зная дифференциальную функцию 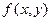 ,можно найти интегральную по формуле :
,можно найти интегральную по формуле : 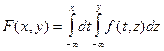
Вероятность попадания случайной точки (X,Y) в область 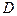 определяется равенством
определяется равенством 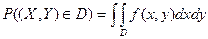
Свойства дифференциальной функции :
1. 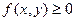
2. 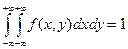
Если составляющие X и Y дискретны и их возможные значения : 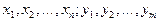 условным распределением составляющей X при
условным распределением составляющей X при 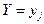 называют совокупность условных вероятностей
называют совокупность условных вероятностей 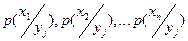 , где
, где 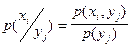
Если X и Y непрерывны,то условной дифференциальной функцией 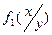 составляющей
составляющей 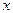 при заданном значении
при заданном значении 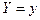 называют отношение дифференциальной функции системы к дифференциальной функции составляющей
называют отношение дифференциальной функции системы к дифференциальной функции составляющей 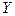 :
: 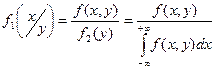
аналогично, 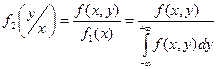
Величины X и Y являются независимыми,если условные дифференциальные функции случайных величин X и Y равны их безусловным дифференциаль-
ным функциям.
Числовые характеристики системы случайных величин :
для непрерывной системы :
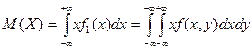
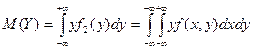
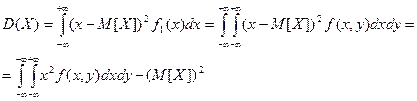
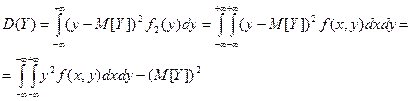
корреляционный момент системы (X,Y) 
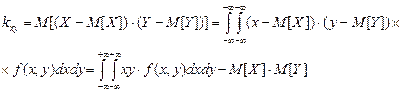
для дискретной системы :
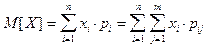
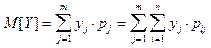
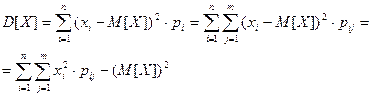
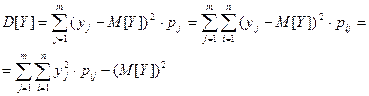
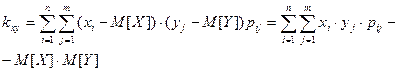
Коэффициент корреляции (служит для оценки тесноты линейной связи
между X и Y ) 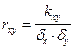
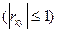
Если 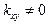 ,то X и Y называют коррелированными. Из коррелированности X и Y следует их зависимость,из независимости X и Y следует их некоррелированность.
,то X и Y называют коррелированными. Из коррелированности X и Y следует их зависимость,из независимости X и Y следует их некоррелированность.
Корреляционная матрица системы двух случайных величин X и Y: 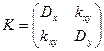
7.1.По некоторой цели производится 2 выстрела. Вероятность попадания при одном выстреле равна 0,7. Составить закон распределения системы случайных величин (X,Y), считая ,что X-число попаданий,а Y-число промахов.
Решение : случайные величины X и Y могут принимать значения 0,1,2. Заметим,что
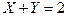 и
и 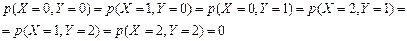
как вероятности невозможных событий. Введём события 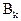 ={попадание при k-том выстреле},k=1,2.
={попадание при k-том выстреле},k=1,2. 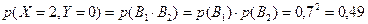
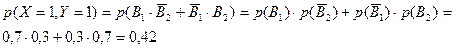
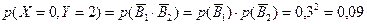
 X Y X Y | |||
| 0,49 | |||
| 0,42 | |||
| 0,09 |
7.2. Система дискретных случайных величин (X,Y) имеет закон распределения :
 X Y X Y | |||
| -2 | 0,1 | 0,05 | 0,2 |
| 0,1 | 0,1 | 0,2 | |
| 0,1 | 0,05 | 0,1 |
Найти : а) законы распределения составляющих X и Y;б) условный закон распределения составляющей X,при условии,что Y приняла значение 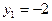 ;в) условный закон распределения составляющей Y при условии,что X приняла значение
;в) условный закон распределения составляющей Y при условии,что X приняла значение 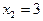 ;г) функции распределения составляющих X и Y;д) условные функции распределения составляющих
;г) функции распределения составляющих X и Y;д) условные функции распределения составляющих 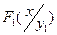 и
и 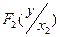 .
.
Решение :
a)
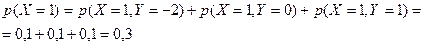
Аналогично находим 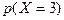 и
и 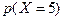
| X | Y | -2 | ||||||
| p | 0,3 | 0,2 | 0,5 | p | 0,35 | 0,4 | 0,25 |
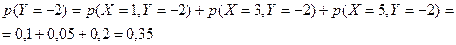
Аналогично находим 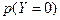 и
и 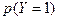
б) 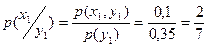 ;
; 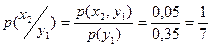 ;
; 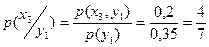

| X | |||
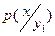 | 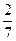 | 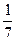 | 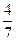 |
в) 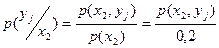
| Y | -2 | ||
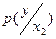 | 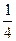 | 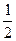 | 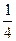 |
г) 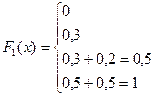
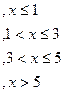
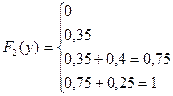
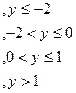
д) 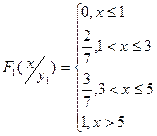

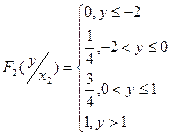
7.3.Даны ряды распределения составляющих X и Y системы независимых дискретных случайных величин. Найти : а) закон распределения 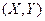 ;б) функции распределения составляющих
;б) функции распределения составляющих 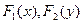 ;в) функцию распределения системы
;в) функцию распределения системы 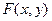 :
:
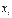 | 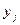 | -2 | ||||||
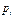 | 0,3 | 0,2 | 0,5 | 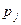 | 0,35 | 0,4 | 0,25 |
Решение :
а) применяя теорему умножения для независимых событий, получим 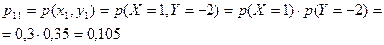
и т.д.
 X Y X Y | |||
| -2 | 0,105 | 0,07 | 0,175 |
| 0,12 | 0,08 | 0,2 | |
| 0,075 | 0,05 | 0,125 |
б) 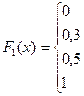
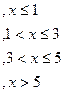
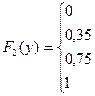
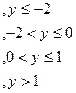
для системы независимых случайных величин X и Y 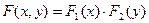
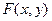 :
:
 X Y X Y | 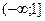 | 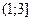 | 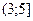 | 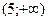 |
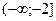 | ||||
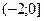 | 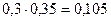 | 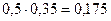 | 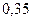 | |
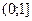 | 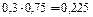 | 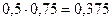 | 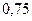 | |
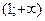  | 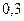 | 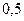 | 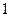 |
7.4. Распределение вероятностей случайной величины 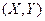 задано таблицей
задано таблицей
 X Y X Y | -1 | ||
| 0,1 | 0,3 | 0,1 | |
| 0,2 | |||
| 0,1 | 0,2 |
Определить математические ожидания и корреляционную матрицу данных величин, коэффициент корреляции. Зависимы ли X и Y ?
Решение:
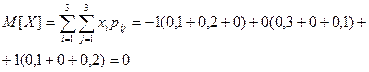
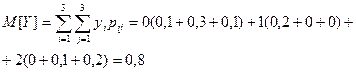
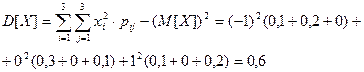
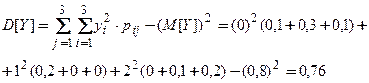
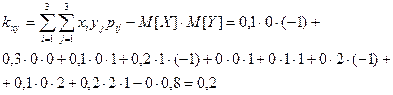
 ,следовательно X и Y коррелированы.
,следовательно X и Y коррелированы. 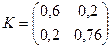
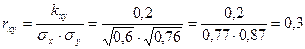 . X и Y зависимы , т.к. из коррелированности следует зависимость.
. X и Y зависимы , т.к. из коррелированности следует зависимость.
7.5. Имеется урна с 3 белыми и 3 чёрными шарами. Производится последовательное извлечение шаров (без возвращения ) до первого появления белого шара,X-число извлечённых шаров. Далее извлечение продолжается до первого появления чёрного шара :
Y-число шаров,извлечённых во второй серии. а) Требуется составить закон распределения 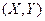 . б) Описать законы распределения отдельных случайных компонент X и Y. в) Описать условный закон распределения случайной величины X при условии Y=2 и при этом условии вычислить условное математическое ожидание
. б) Описать законы распределения отдельных случайных компонент X и Y. в) Описать условный закон распределения случайной величины X при условии Y=2 и при этом условии вычислить условное математическое ожидание 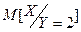 . г) Вычислить основные характеристики случайного вектора :
. г) Вычислить основные характеристики случайного вектора : 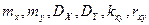 .д) Найти функцию распределения составляющей X и условную функцию распределения
.д) Найти функцию распределения составляющей X и условную функцию распределения 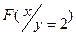 .
.
Решение : Для описания закона распределения дискретного случайного вектора 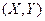 необходимо определить множество всех возможных пар значений
необходимо определить множество всех возможных пар значений 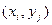 и соответствующие вероятности. Результат удобно представить в виде следующей таблицы :
и соответствующие вероятности. Результат удобно представить в виде следующей таблицы :
 X Y X Y | 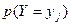 | ||||
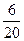 | 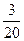 | 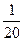 | 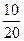 | ||
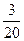 | 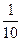 | 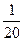 | 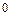 | 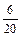 | |
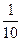 | 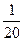 | 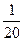 | 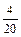 | ||
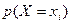 | 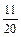 | 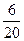 | 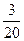 | 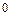 |
а) Применяя теорему умножения для зависимых событий,получим 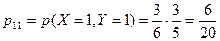 ;
;
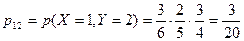 ,
, 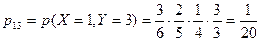 ;
; 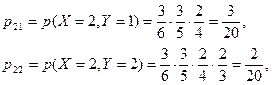
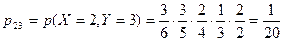 ;
; 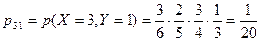 ;
; 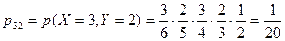 ,
, 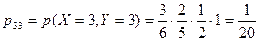 ;
; 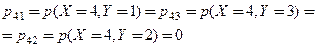 как вероятности невозможных событий.
как вероятности невозможных событий.
б) 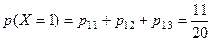 ,аналогично найдём
,аналогично найдём
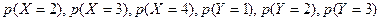
 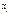 | 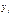 | ||||||||
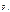 | 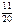 | 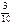 | 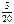 | 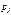 | 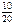 | 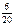 |  |
в) Условный закон распределения случайной компоненты X при условии,что компонента Y приняла значение равное 2,находим по формуле 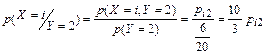 ,результат оформим в виде таблицы
,результат оформим в виде таблицы
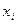 | ||||
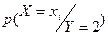 | 1/2 | 1/3 | 1/6 |
при этом математическое ожидание 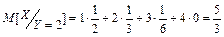
г) искомые характеристики вычислим по известным формулам 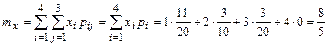
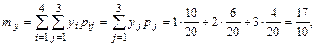
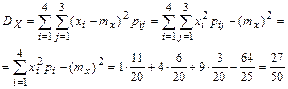 , аналогично
, аналогично 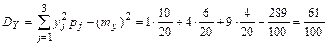 ,
, 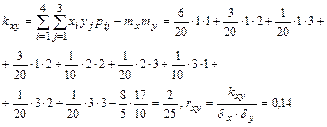
д) 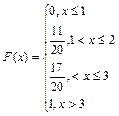
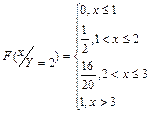
7.6. Задана дифференциальная функция системы случайных величин 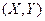 :
: 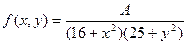 .
.
Найти A.
Решение : А найдём из свойства 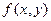 ,что
,что 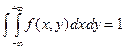 ,
,
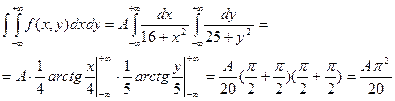


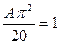 ,
, 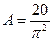
7.7. Задана интегральная функция двумерной случайной величины
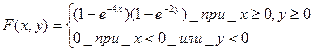
Найти дифференциальную функцию системы (X,Y) и вероятность попадания случайной точки 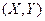 в область D:
в область D: 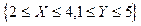 .
.
Решение:
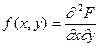

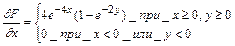
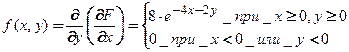
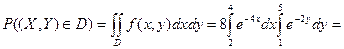
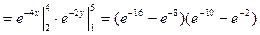
7.8. Дана дифференциальная функция системы двух случайных величин
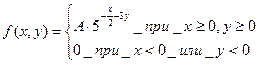
Найти параметр А и интегральную функцию системы F(x,y).
Решение:
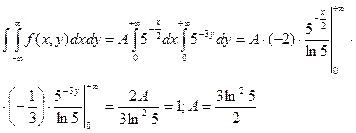
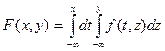
1)x<0 или y<0
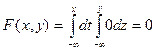
2) 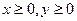
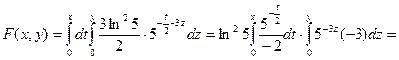
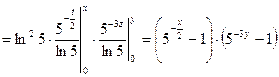
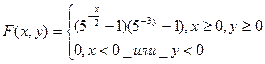
7.9.Дана дифференциальная функция системы двух случайных величин (X,Y)
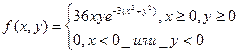
Доказать, что составляющие X и Y независимы.
Решение:
Найдем дифференциальную функцию составляющей Х
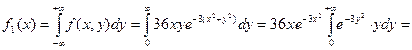
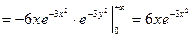 при
при 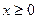
аналогично
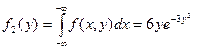 при
при 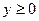
Найдем условные дифференциальные функции составляющих:
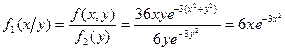 при
при 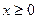
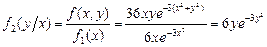 при
при 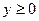
X и Y независимы, т.к. 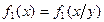 ,
, 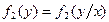
7.10. Система двух непрерывных случайных величин X и Y, равномерно распределена внутри прямоугольного треугольника Д с вершинами О (0,0), А (0,8), В (8,0).
Найти: а) дифференциальную функцию системы;
б) дифференциальные и условные дифференциальные функции составляющих; в) зависимы ли X и Y?
Решение:

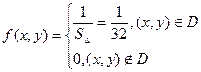


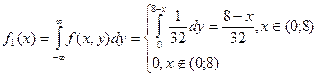
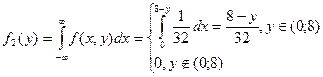

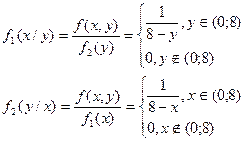
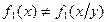
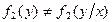
X и Y зависимы.
7.11. Случайная точка (X,Y) распределена с постоянной плотностью внутри квадрата R
 Написать выражение плотности распределения f(x,y), плотностей распределения
Написать выражение плотности распределения f(x,y), плотностей распределения 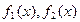 отдельных величин X,Y , входящих в систему; условных плотностей
отдельных величин X,Y , входящих в систему; условных плотностей 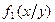 и
и 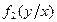 . Зависимы или независимы случайные величины X,Y?
. Зависимы или независимы случайные величины X,Y?
Решение: площадь квадрата равна 2 ( диагональ =2),поэтому
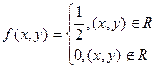
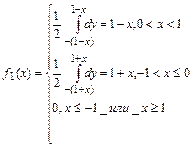

т.е.
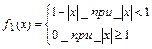
аналогично
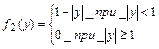
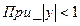
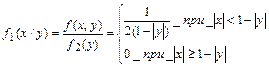
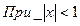

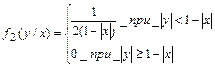
X и Y зависимы.
7.12. Коэффициенты 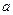 и
и 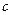 квадратного уравнения
квадратного уравнения 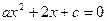 наудачу и независимо друг от друга выбираются из отрезка [0;2]. Найти вероятность того, что корни этого уравнения окажутся действительными.
наудачу и независимо друг от друга выбираются из отрезка [0;2]. Найти вероятность того, что корни этого уравнения окажутся действительными.
Решение:
Слово “наудачу” означает, что каждая из случайных величин 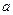 и
и 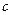 имеет равномерное распределение на [0;2].
имеет равномерное распределение на [0;2].
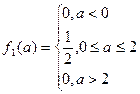
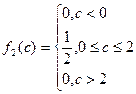
Случайные величины 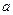 и
и 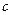 независимы, поэтому
независимы, поэтому
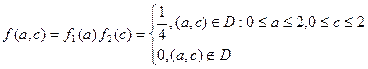
Корни действительны тогда и только тогда, когда дискриминант 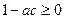 , т.е.
, т.е. 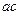
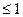 .
.
 Неравенство
Неравенство 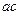
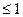 выполняется для точек квадрата D, принадлежащих областям
выполняется для точек квадрата D, принадлежащих областям 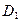 и
и 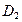 .
.
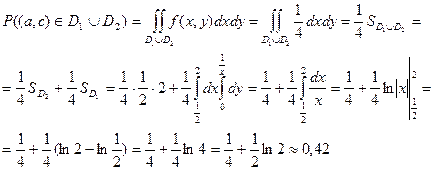
7.13. Найти числовые характеристики и построить корреляционную матрицу для системы двух случайных величин (X,Y), заданную плотностью вероятностей
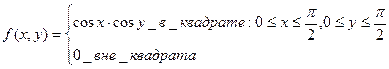
Решение:
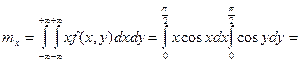
 |  |
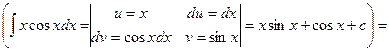
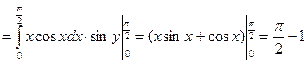
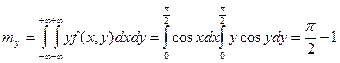
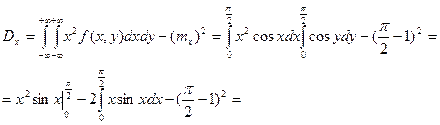


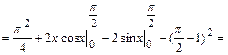
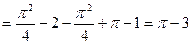
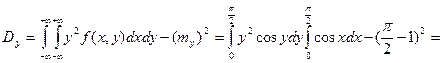
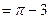
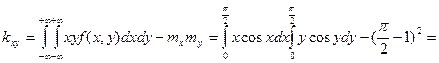
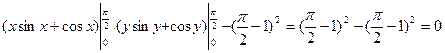
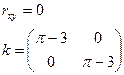
7.14. Задана дифференциальная функция системы двух случайных
величин (X,Y)
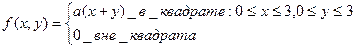

Найти 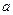 , интегральную функцию системы F(x,y), P(0<X<2, -1<Y<2), числовые характеристики
, интегральную функцию системы F(x,y), P(0<X<2, -1<Y<2), числовые характеристики 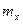 ,
, 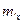 ,
, 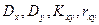 ; плотности распределения составляющих; условные плотности распределения
; плотности распределения составляющих; условные плотности распределения 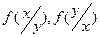 .
.
Решение:  найдем из свойства дифференциальной функции
найдем из свойства дифференциальной функции
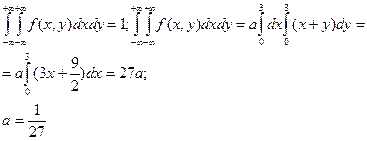
a) x<0 или y<0
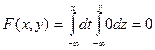
б) 0£x£3, 0£y£3
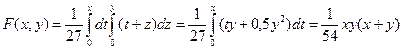

в) 0£x£3, y>3
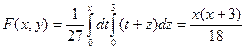
г) x>3, 0£y£3
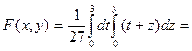
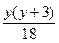
д) x>3, y>3
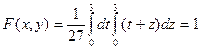
Итак,
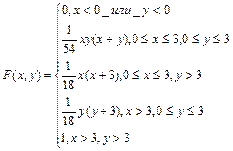
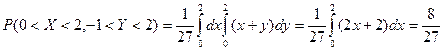

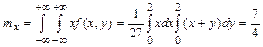
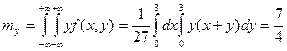
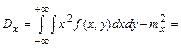
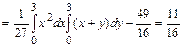
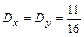

 |
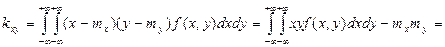
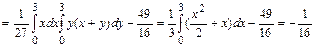
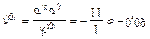
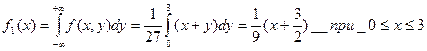

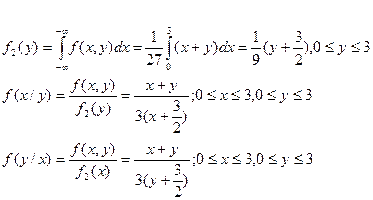
7.15. В первом ящике  6 шаров, во втором также 6 шаров.
6 шаров, во втором также 6 шаров.
1 ящик: 1 шар с №1, 2 шара с №2, 3 шара с №3. 2 ящик: 2 шара с №1, 3 шара с №2, 1 шар с №3. Пусть Х - номер шара, вынутого из 1 ящика, Y - номер шара, вынутого из 2 ящика. Из каждого ящика вынули по шару. Составить таблицу закона распределения системы случайных величин (X,Y).
Ответ:
 X Y X Y | |||
| 1 | 1 | 1 | |
| 1 | 1 | 1 | |
| 1 | 1 | 1 |
7.16.Задано распределение вероятностей дискретной двумерной случайной величины:
