III Интегральное исчисление
- Первообразная функции
Опр. Функция F(x) над первообразной функции F(x) на некотором промежутке, если для всех x из этого промежутка 
Пр: 1) F(x)=sin x – первообр. F(x)=cosx , т.к. 
2) 
- первооб. 
,т.к 
.
Задача Док – ть, что F(x) – первооб. F(x)
1. 
3. 
2. 
4. 
Неопределенный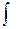 
. Его свойства.
Опр. Интегрирование – это процесс нахождения первообразованых
Опр. Множество первообразованых для данной функции F(x) над неопределенным интегралом и обозначается 
Пр. 
Таблица неопределенных интегралов
-
. -
. -
. -
. -
. -
. -
. -
. -
. -
. -
.
12. 
.
13. 
.
14. 
Свойства неопределенного интеграла:
- Если
– постоянная величина, то 
. -
-
. -
. -
.
Задача: Вычислить неопределенный интеграл.
Задача. Вычислить неопределенный интеграл.
Определенный интеграл. Вычисление площадей плоских фигур.
Опр. Фигура, ограниченная снизу отрезком 
оси ох, сверху
графиком функции 
, с боков отрезками х=а, х=b,
 | |||
 | |||
называется криволинейной трапецией.
Площадь криволинейной трапеции вычисляется по формуле:
Таким образом, вычисление площади криволинейной трапеции сводится к отысканию первообразной F(x) функции , т.е. к интегрированию F(x).
Опр. 6.2. Разность 
называется интегралом от функции F(x) и обозначается 
.
- формула Ньютона – Лейбница.
Пример. Найти площадь фигуры, ограниченной графиком 
Свойства определенного интеграла аналогичны свойствам неопределенного интеграла.
Метод замены переменной (метод подстановки).
Существует три метода вычисления интегралов: непосредственное интегрирование, метод замены переменной, метод интегрирования по частям.
Пример.
Дифференциальные уравнения.
Опр. Диф.уравнением называется уравнение, связывающее функцию , переменную x и производную f(x).
Опр. Если функция зависит только от переменной x, то диф.урав. называется обыкновенным.
Общий вид обыкновенного диф.уравнения. 
.
Опр. . Максимальный порядок входящих в уравнение производных называется порядком диф.уравнения.
-диф.уравнение первого порядка.
- диф. Уравнение второго порядка.
Решить диф.уравнение – значит найти первообразную функции f(x), т.е. вычислить неопределенный интеграл от F(x).
Пусть дано диф.ур. первого порядка 
, необходимо его решить.
общее решение диф.уравнения.
Алгоритм решения диф.уравнений:
1. 
2. домножаем обе части уравнения на 
и переносим слагаемые с в другую сторону.
3. Переменные, содержащие x переносим к , а переменные, содержащие y к 
.
4. Интегрируем обе части уравнения.
Пример. Решить диф.уравнение.
Уравнению вида можно придать вид
Опр.. Уравнение (*) называется уравнением с разделяющимися переменными, а уравнение (**) – уравнением с разделенными переменными.
Пример. 