III. Методика измерений и расчетные формулы.

Звуковая волна в газе представляет собой продольную волну в упругой среде, в которой происходят периодические сжатия и разрежения газа, например воздуха. Как известно из механики, скорость распространения упругих колебаний определяется выражением:

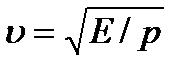
гдеЕ – модуль упругости среды, ρ– плотность среды.

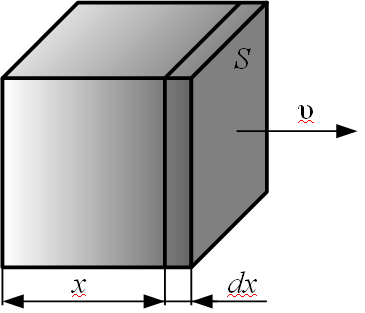
Воспользуемся уравнениями термодина-мики для нахождения скорости звука в газе. Выделим мысленно в газе прямоугольный параллелепипед, площадь основания которого S, a высота – x, параллельная вектору скорости распространения волны (см. рис.6а).

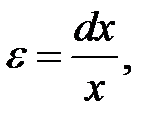
Рисунок 6а – К выводу скорости звука в газе.

Этот параллелепипед будет испытывать продольную деформацию dx, причём относительная деформация согласно закону Гука:

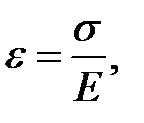
где s – сила давления, испытываемая единицей поверхности выбранного объёма.

В данном случае:

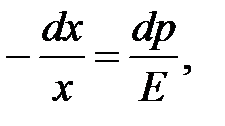
где dp– давление, избыточное над равновесным.

Умножим и разделим левую часть на S:

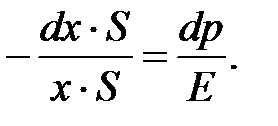
Последнее выражение можно представить в виде:

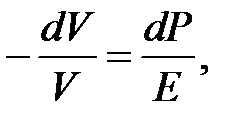
где dV и V – изменение объема и объём параллелепипеда. Отсюда:

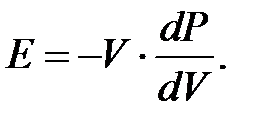
Так как звуковые колебания имеют довольно высокую частоту (сотни и ты­сячи герц), а теплопроводность газа относительно мала, то смены сжатия и разрежения в газе происходят настолько быстро, что процесс можно считать адиабатным (PV^g= const, g – коэффициент Пуассона). Отсюда получаем:

PgV^g-1dV + V^gdP = 0 ,

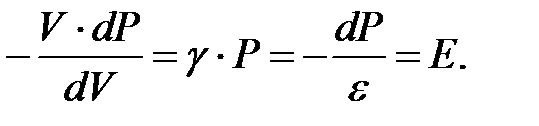
Умножая и деля последнее выражение на молярный объём V_m и используя уравнение Менделеева – Клапейрона, получаем окончательное выражение для зависимости скорости звука в газе от температуры:

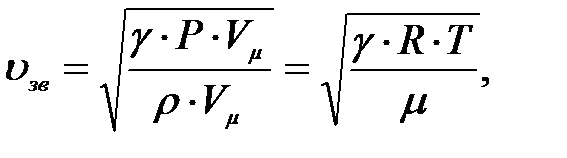(1)

где m – молярная масса газа, R – универсальная газовая постоянная, Т – абсолютная температура газа.

Подставляя в последнюю формулу значения величин для воздуха и заменяя абсолютную температуру температурой t по шкале Цельсия, получим удобное для практического применения соотношение:

u_зв= 331,6+0,6×t.

Действие установки основано на использовании явления звукового резонанса (стоячей волны) в трубке с закрытыми торцами. Известно, что в замкнутой среде на границе раздела двух сред бегущая волна отражается, и в результате в этой среде возникают две встречные когерентные волны, которые при наложении интерферируют. Уравнения прямой и обратной волн без учёта потерь энергии могут быть записаны в следующем виде:

S₁ = А sin(ωt – kx + a₁) и S₂ = А sin(ωt + kx + a₂),

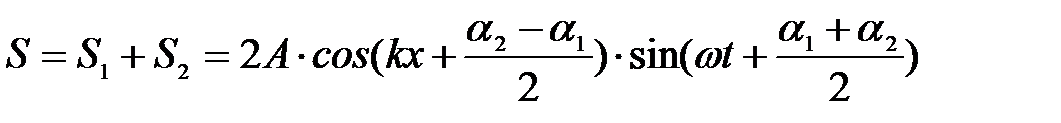
где А – амплитуда, ω – циклическая частота, a – начальная фаза колебаний, k – волновое число. При наложении этих волн получается результирующее колебание.

Пусть a₁ = 0 и a₂ – a₁ = p, тогда уравнение стоячей волны примет вид:

S = 2Аsin(kx)×cos(ωt).

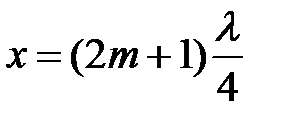
В множителе, зависящем от времени, нет координаты, т.е. все точки волны одновременно проходят положение равновесия, а амплитуда стоячей волны, в отличие от бегущей, зависит от координаты. Точки, соответствующие максимуму амплитуды, называются пучностями, а точки, соответствующие минимуму амплитуды, называются узлами стоячей волны. Координаты пучностей находятся из условия sinkx =1:

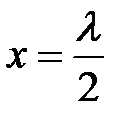
где l – длина волны, m = 0, 1, 2, …

Координаты узлов находятся из условия sin(kx) =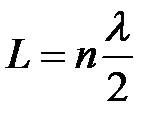

Между длиной стоячей волны и размерами среды существует вполне определённое соотношение. В замкнутом с обеих сторон столбе воздуха стоячая волна возникает только в том случае, если на длине столба L укладывается целое число полуволн:

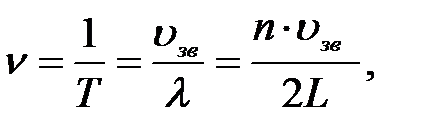
где n – положительное целое число, номер резонанса.

Из этого соотношения можно найти частоты волн, при которых возможно образование стоячей волны.

Частота, соответствующая n = 1, называется основной, остальные, кратные основной, называются гармониками.

В данной работе в одном конце трубки воздуха располагается источник колебаний звуковой частоты (телефон), а в другом – приемник (микрофон). Если в трубке при соответствующей частоте колебаний источника возникает стоячая волна, то амплитуда звуковых колебаний, воспринимаемых микрофоном в противоположном от телефона торце трубки, резко возрастает, что фиксируется максимальным отклонением стрелки микроамперметра и резким возрастанием амплитуды сигнала на осциллографе. Поэтому, измеряя частоту n, соответствующую резонансу, можно определить скорость звука по формуле:

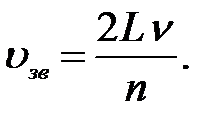(2)

Установка позволяет устанавливать температуру воздуха в волноводе от комнатной до 70 °С и получать резонансы с порядками n ≥ 2.