Повышение точности результатов измерения маркетинговых исследований

При построении эконометрических моделей и сборе первичных данных наиболее распространенным методом является метод экспертной оценки. Основным преимуществом этого метода является его простота, где основная измерительная процедура осуществляется с помощью эксперта – человека. Однако наряду с простотой он обладает большой погрешностью измерения. При построении моделей маркетинговых процессов возникают различного рода погрешности, обусловленные человеческим фактором, которые ведут к неверному принятию решений в процессе управления социально-экономическими системами [2,3,4].

Известны различные способы для сбора и обработки информации с помощью метода экспертных оценок.

Недостатком известных способов для их осуществления является невысокая достоверность результатов измерений, обусловленная субъективной оценкой человеческого фактора.

Указанная задача решается за счет того, что в существующий метод экспертной оценки вводится тест, который используется в алгоритме повышения точности результатов измерения для компенсации погрешности.

Известно, что обобщенную характеристику измерительного процесса можно представить в виде

f = F (у, а …в) (5.11)

где у – измеряемая величина; а … в - параметры измеряемой величины.

Под действием внешних и внутренних факторов на измерительный процесс, параметры, а…в изменяют свои значения, что приводит к погрешности измерения.

В общем случае при тестовых методах повышения точности измерений процесс состоит из нескольких тактов. Сначала измеряется основная величина, затем тесты - Q, каждый из которых является некоторой функцией измеряемой величины - у. Результаты основного и дополнительного измерений формируют так называемый тестовый алгоритм, который позволяет обеспечить повышение точности результатов измерения того или иного процесса.

Построение прогноза социально-экономического процесса описывается трендом, который можно записать в виде идеальной характеристики

Y_и= Ахⁿ, (5.12)

где х – временной интервал,

А - параметры тренда.

Блок схема способа измерения и компенсации мультипликативной грешности представлена на рис.5.3 и состоит из:

блока измерения (БИ);

тестового блока (ТБ);

блока формирования полинома измерения (БФП);

первого блока умножения (БУ 1);

первого блока памяти (БП 1);

второго блока памяти (БП 2);

третьего блока памяти (БП 3);

блока деления (БД);

четвертого блока памяти (БП 4);

пятого блока памяти (БП5);

второго блока умножения (БУ 2).

Алгоритм повышения точности измерения и компенсации мультипликативной погрешности работает следующим образом.

Этап

Осуществляется измерение БИ реальной характеристики социально-экономического процесса. В процессе измерения возникает мультипликативная погрешность а, которая приводит к искажению результатов измерения

Y_р = Аахⁿ (5.13)

где а - мультипликативная погрешности измерения

Полученный результат запоминается в блоке памяти БП1

Этап

Вводится тест Q из ТБ и полином n степени из БПФ в первый блок умножения БУ1, на выходе которого получим значение Qхⁿ , которое запомнится в третьем блоке памяти БП3, а так же поступит на вход БИ для проведения измерения тестовой величины вместе с мультипликативной погрешностью а

Y_т = Qахⁿ (5.14)

Это значение запомниться во втором блоке памяти БП2.

Этап

Найдем соотношение реальной характеристики Y_р и тестовой величины Y_т путем деления уравнения (5.12) на (5.14) в блоке деления БД

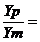
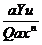
(5.15)

Полученная информация запишется в блок памяти БП4.

Как видно из уравнения (5.15) мультипликативная погрешность а здесь компенсируется.

Этап

Во втором блоке умножения БУ2 осуществляется операция перемножения (5.15) на Qхⁿ в результате чего получаем расчетное значение измеряемой величины Y_ras с компенсацией погрешности измерения а, которое будет идентично идеальной характеристики Y_и , результат запомнится в блоке памяти БП5.

Y_и = Y_ras = 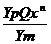(5.16)

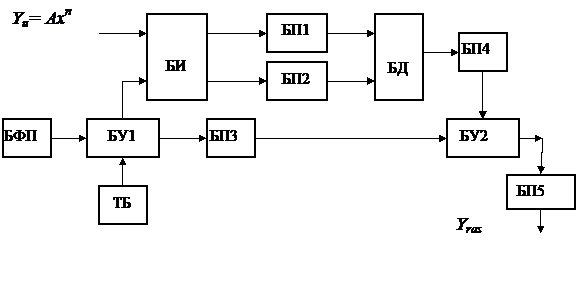
Рис. 5.3. Блок схема способа компенсации мультипликативной погрешности измерения