Корректировка прогноза с учетом тренда и сезонности

При прогнозировании можно учесть не только тренд, но и сезонные колебания спроса. Прежде чем использовать модель, которая рассмотрена в следующем примере, следует проверить временной ряд на выполнение следующих двух условий:

1. Сезонные пики и падения спроса должны четко проглядываться на статистическом ряде, т.е. они должны быть больше, чем случайные колебания спроса (так называемый «шум»).

2. Сезонные пики и падения спроса должны устойчиво повторяться из года в год.

Если эти два условия не соблюдаются, то есть сезонные колебания неустойчивы, незначительны и трудно отличаются от «шума», то использовать модель для точного прогноза спроса на следующий временной период будет крайне трудно. Если условия выполняются и в модели устанавливается высокое значение сглаживающей постоянной, чтобы учитывать большую амплитуду колебаний спроса, то имеет смысл усложнить модель.

В этой новой модели прогноз строится с учетом корректировок тренда и сезонности, которые отображаются в форме индексов. Это позволяет достичь высокой точности прогноза.

Уравнения усложненной модели:

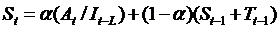
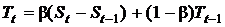
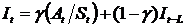
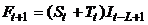
где Т_t – тренд в период t, S_t – начальный прогноз в период t, F_t+1 – прогноз на период t+1 с учетом тренда и сезонности, I_t –индекс сезонных колебаний в период t, L – временной период, в течение которого совершается полный сезонный цикл, g – сглаживающая постоянная для сезонного индекса.

Пример. Рассчитаем прогноз на третий квартал текущего года с учетом тренда :

	Квартал
I	II	III	IV
Прошлый год	1 200			1 100
Текущий год	1 400	1 000	F3 = ?

Для начала рассчитаем прогноз на первый квартал текущего года. В качестве исходных значений при расчетах будем использовать S_t-1 = 975 (средний спрос за квартал по данным предыдущего года) и T_t-1 = 0 (тренд отсутствует). Допустим, что сглаживающие постоянные a = 0,2 и b = 0,3, а g = 0,4. Теперь начнем расчеты.

Прогноз на первый квартал текущего года:

S₀ = 975 и T₀ = 0. Тогда:

F₁ = (975 + 0) ´ 1,23 = 1200, потому что I₁ = 1200 / 975 = 1,23

И тогда:

Прогноз на второй квартал текущего года:

S₁ = 0,2´1400 / 1,23 + 0,8´(975 + 0) = 1007,5

I₁ = 0,4´1400 / 1007,5 + 0,6´1,23 = 1,29

Т₁ = 0,3´(1007,5 – 975) + 0,7´0 = 9,75

F₂ = (1007,5 + 9,75)´0,72 = 730,3, потому что I₂ = 700 / 975 = 0,72

Прогноз на третий квартал текущего года:

S₂ = 0,2´1000 / 0,72 +0,8´(1007,5 + 9,75) = 1092,4

I₂ = 0,4´1000 / 1092,4 + 0,6´0,72 = 0,8

Т₂ = 0,3´(1092,4 – 1007,5) + 0,7´9,75 = 32,3

F₂ = (1092,4 + 32,3)´0,92 = 1005, потому что I₃ = 900 / 975 = 0,92

В итоге получаем:

	Квартал
I	II	III	IV
Прошлый год	1 200			1 100
Текущий год	1 400	1 000
Прогноз	1 200		1 005

Ошибка прогнозирования

Поскольку будущее никогда нельзя в точности предугадать по прошлому, то прогноз будущего спроса всегда будет содержать в себе ошибки в той или иной степени. Модель экспоненциального сглаживания прогнозирует средний уровень спроса. Поэтому следует построить модель так, чтобы уменьшить разность между прогнозом и фактическим уровнем спроса. Эта разность называется ошибкой прогнозирования.

Ошибка прогнозирования выражается такими показателями, как среднеквадратическое отклонение, вариация или среднее абсолютное отклонение. Раньше среднее абсолютное отклонение использовалось в качестве основного измерителя ошибки прогнозирования при использовании модели экспоненциального сглаживания. Среднеквадратическое отклонение отвергли из-за того, что рассчитывать его сложнее, чем среднее абсолютное отклонение, и у компьютеров на это просто не хватало памяти. Сейчас у компьютеров достаточно памяти, и теперь среднеквадратическое отклонение используется чаще.

Ошибку прогнозирования можно определить с помощью следующей формулы:

ОШИБКА ПРОГНОЗА = ФАКТИЧЕСКИЙ СПРОС – ПРОГНОЗ СПРОСА

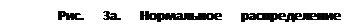
Если прогноз спроса представляет собой среднее арифметическое фактического спроса, то сумма ошибок прогнозирования за определенное количество временных периодов будет равна нулю. Следовательно, значение ошибки можно отыскать путем суммирования квадратов ошибок прогнозирования, что позволяет избежать взаимного устранения положительных и отрицательных ошибок прогнозирования. Эта сумма делится на количество наблюдений и затем из нее извлекается квадратный корень. Показатель корректируется с уменьшением одной степени свободы, которая теряется при составлении прогноза. В результате, уравнение среднеквадратического отклонения имеет вид:

,

где S_E – средняя ошибка прогнозирования; A_i – фактический спрос в период i; F_i – прогноз на период i; N – размер временного ряда.

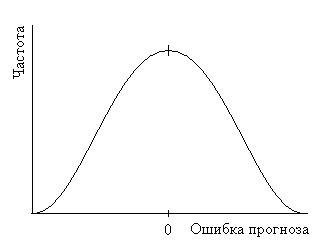
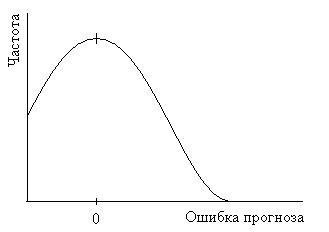
Форма распределения ошибок прогнозирования является важной, когда формулируются вероятностные утверждения о степени надежности прогноза. Две типовые формы распределения ошибок прогнозирования показаны на рисунке 3.

Полагая, что модель прогнозирования отражает средние значения фактического спроса достаточно хорошо и отклонения фактических продаж от прогноза относительно невелики по сравнению с абсолютной величиной продаж, то вполне вероятно предположить нормальное распределение ошибок прогнозирования. В тех же случаях, когда ошибка прогнозирования сопоставима по величине с величиной спроса, имеет место скошенное, или усеченное нормальное распределение ошибок прогноза.

Определить тип распределения в конкретной ситуации можно с помощью теста на соответствие критерию согласия хи-квадрат. В качестве альтернативы можно использовать другой тест, с помощью которого можно определить, является ли распределение симметричным (нормальным) или экспоненциальным (разновидность скошенного распределения):

При нормальном распределении около 2% наблюдаемых значений превышают значение, равное сумме среднего и удвоенного значения среднеквадратического отклонения. При экспоненциальном распределении около 2% наблюдаемых значений превышают среднее на величину среднеквадратического отклонения, умноженного на коэффициент 2,75. Следовательно, в первом случае используется нормальное распределение, а во втором случае – экспоненциальное.

Пример. Снова вернемся к нашему примеру. В базовой модели экспоненциального сглаживания были получены следующие результаты:

	Квартал
I	II	III	IV
Прошлый год	1 200			1 100
Текущий год	1 400	1 000	F3 = ?
Прогноз	1 200		1 005

Оценим стандартную ошибку прогнозирования по данным за первый и второй кварталы текущего года, по которым нам известны фактические и прогнозные значения. Допустим, что спрос имеет нормальное распределение относительно прогноза. Рассчитаем границы доверительного интервала с вероятностью 95% для третьего квартала.

Стандартная ошибка прогнозирования:

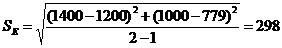
Используя таблицу А (см. Приложение I), определяем коэффициент z_95% = 1,96 и получаем границы доверительного интервала по формуле:

Y = F₃ ± z(S_E) =1005 ± 1,96´298 = 1064 ± 584,2

Следовательно, с 95%-й вероятностью границы доверительного интервала прогноза спроса на третий квартал текущего года составляют значения:

420,8 < Y < 1589,2