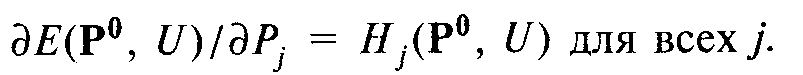Задача максимизации полезности

Если рассматривать эту задачу как задачу на условный экстремум, то ее решение м.б. геометрическим: двигаясь по линиям безразличия на «северо-восток» до упора, выбираем линию безразличия, которая имеет с бюджетной прямой точку касания (х1, х2) – этот набор называется локальным рыночным равновесием.

Графическое решение:

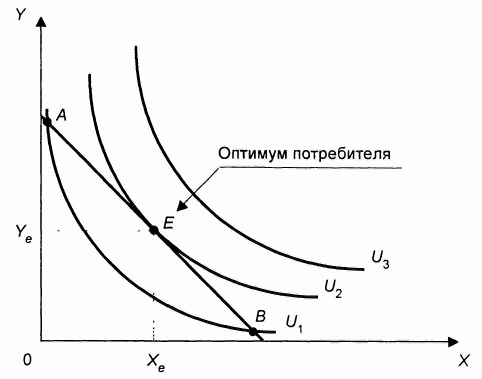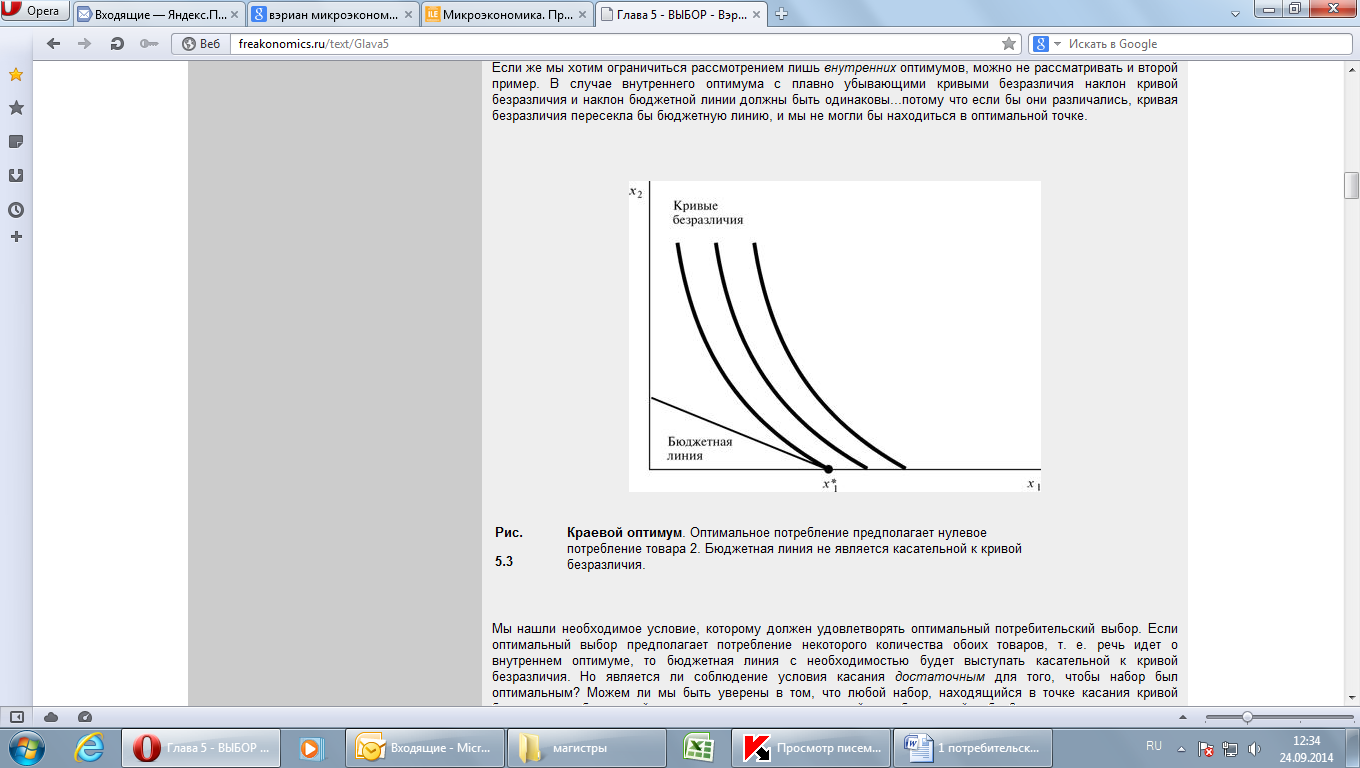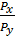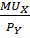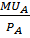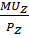В точке оптимума наклон линии бюджетного ограничения ( ) равен наклону касательной к кривой безразличия (MRSxy), следовательно для всех покупаемых наборов выполняется правило: = = … = = l	Краевой оптимум. Оптимальное потребление предполагает нулевое потребление товара 2. Бюджетная линия не является касательной к кривой безразличия.	Случай более чем одного касания. Налицо три касания, но лишь две точки оптимума, так что условие касания является необходимым, но не достаточным.
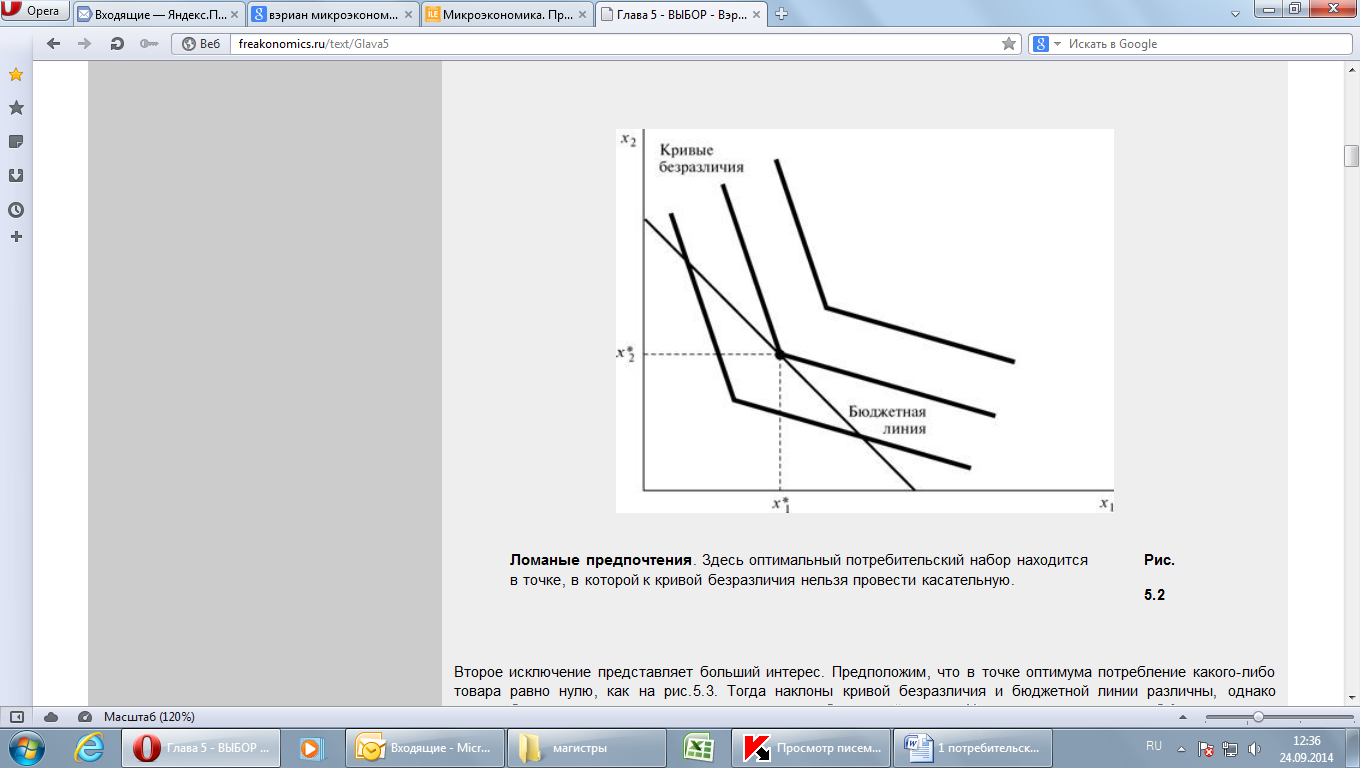Оптимальный выбор в случае вогнутых предпочтений. Оптимальный выбор представлен не точкой внутреннего касания X, а точкой краевого равновесия Z, поскольку Z лежит на более высокой кривой безразличия.	Ломаные предпочтения. Здесь оптимальный потребительский набор находится в точке, в которой к кривой безразличия нельзя провести касательную.

Цена всего товарного набора характеризуется ценностью последней (предельной) единицей блага, что демонстрирует парадокс воды и алмаза.

Если, предпочтения обладают свойством гомотетичности и выполняется аксиома строгой выпуклости, то оптимум будет внутренний. Гомотетичность означает, что MRS одинакова для всех точек, вдоль проходящего через начало координат луча с положительным наклоном, т.е. кривые безразличия имеют одинаковый наклон. Свойством гомотетичности обладают функции полезности для совершенных субститутов, совершенных комплементов и предпочтений Кобба-Дугласа.

При квазилинейных предпочтениях каждая кривая есть вертикально смещенный вариант одной кривой безразличия Y = K – V(X).

Краевой оптимум:

Аналитическая форма записи задачи:

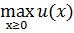
px 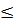I

Задачи на условный экстремум решаются также с помощью функции Лагранжа, которая имеет вид:

L (x1,x2,λ) = U (x1,x2) + λ (I –p1x1 – p2x2)

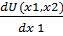– λp1 = 0

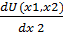– λp2 = 0

I – p1x1 – p2x2 = 0

Решение системы называется критической точкой функции Лагранжа, она может быть записана как (x1,x2,λ) – длинная точка, или (x1,x2) – короткая точка. Координата λ в микроэкономике трактуется как предельная полезность денег.

Cуществует только одна критическая точка – она и будет являться точкой глобального максимума функции.

Если функция полезности дифференцируема, то при условии регулярности мы можем охарактеризовать решение задачи потребителя с помощью условий Куна-Таккера: если х* - решение задачи потребителя при (p,I), то существует множитель Лагранжа λ 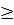0 такой, что для любого товара:

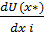
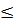λpi

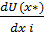
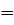λpi , если х* >0

Соответственно внутренне решение характеризуется равенством предельной нормы замещения мжду двумя благами и их относительными ценами:

MRS _ij = =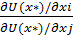

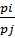
Решая задачу максимизации полезности на бюджетном множестве, получим, что каждой паре (p, I) соответствует множество наилучших при данных ценах и доходе потребительских наборов x (p,I). Функции x1 = D1(p1,p2, I) х2 = D2(p1,p2, I) называются функциями спросапо Маршаллу (по Вальрасу) на первый и второй продукты со стороны потребителя.

В общем виде для n товаров при данной функции полезности выполняется

X* = Dn = (P1, P2, … Pn, I), где Х- величина спроса на товар х, а D- функция спроса.

Функции спроса Di(p1,p2, M), i=1,2 однородны нулевой степени по всем переменным, т.е. для любого числа γ> 0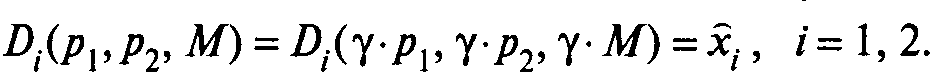

Из задачи потребителя, помимо характеристики спроса, мы получим зависимость полезности от экзогенных параметров, таких как цены и доход, если подставим найденный спрос в целевую функцию. Полученная функция называется косвенной функцией полезности.

Функция 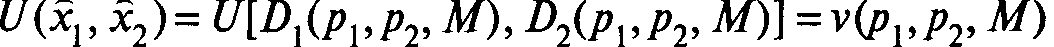называется косвенной (неявной) функцией полезности параметров р1, р2, М; выражение v(p1 p2, M) есть максимум функции полезности.

Свойства косвенной функции полезности v(p₁,p₂, М):

1 Косвенная функция полезности v(p1,p2, M) является однородной функцией нулевой степени по всем переменным р1,р2, М:

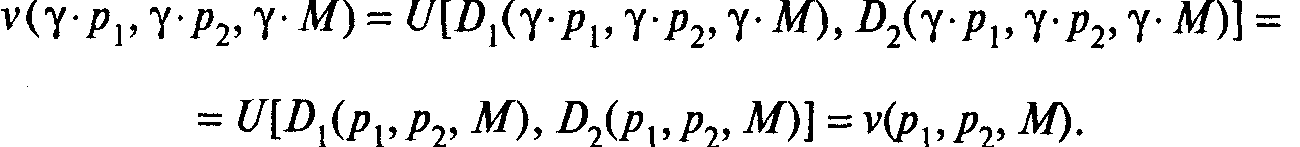
эта однородность объясняется той же причиной, что и однородность функции индивидуального спроса: неизменностью бюджетного ограничения при умножении на положительное число всех его детерменант.

2 Косвенная функция полезности строго возрастает по доходу: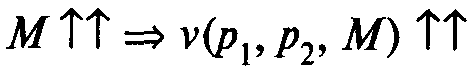

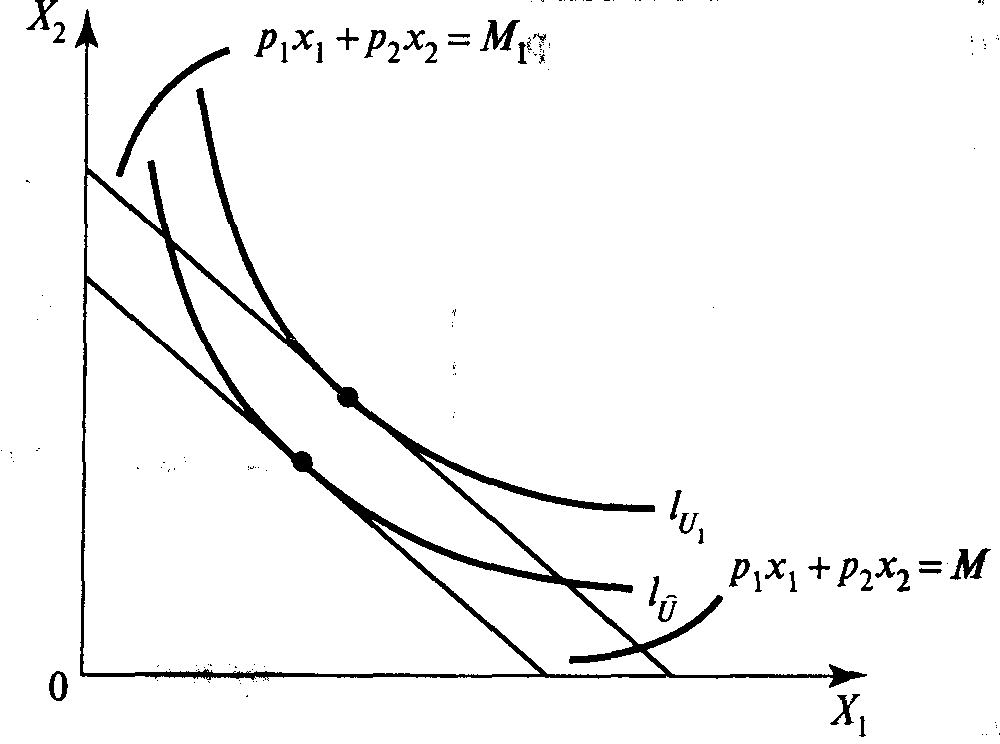
Если M1> M, то v(p1p2, M) > v(p1p2, M1), ибо бюджетная прямая p1x1+p2x2= M1 расположена северо-восточнее бюджетной прямой р1х1 + р2х2 = М, и следовательно, линия безразличия Iu1 расположена северо-восточнее линии безразличия Iu, откуда вытекает неравенство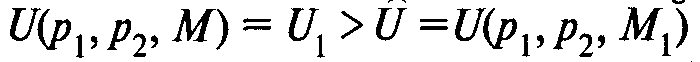

3 Косвенная функция полезности не возрастает по ценам: 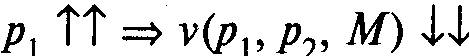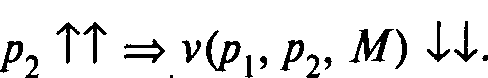Если q1>p1 то τ1= v(q1,p2, M) < v(p1,p2, M) = τ Бюджетное множество для бюджетной линии с более низкими ценами включает в себя множество для бюджетной линии с более высокими ценами, вследствие чего касание с границей второго множества будет никак не выше касания с границей первого.

4. Проекции линии уровня косвенной функции полезности квазивыпуклы к началу координат: в отличие от кривых безразличия, отображающих прямую функцию полезности, и в соответствии со свойством 3 отображаемые уровни полезности нарастают в направлении не от начала координат, а к нему. Это своеобразные кривые безразличия, которые строятся в пространстве товарных цен и именуются «ценовыми кривыми безразличия»

5. Если 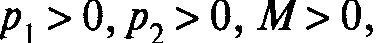, то косвенная функция полезности непрерывная по всем переменным понятие косвенной функции полезности можно применять для изучения налогов и субсидий на уровень полезности, достигаемый индивидом в потреблении. в частности, доказывается принцип преимущества аккордного обложения, согласно которому налоги на совокупный доход снижают данный уровень полезности в меньшей степени, чем налоги на единицу потребления (потоварные налоги), приносящие такую же сумму в бюджет.

6.Предельная полезность по доходу равна производной глобального максимума по параметру I :

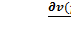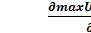= = λ

Это утверждение позволяет оценить новый максимум функции полезности, который получается при относительно малом изменении дохода:

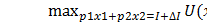
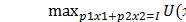+ λ I

7. Если предпочтения локально ненасыщаемы и строго выпуклые и функция v(p,I) дифференцируема при (p,I) >> 0, то выполняется тождество Роя: мерой изменения значения функции полезности в связи с изменением цены является произведение (-хi*λ), i =1,2

= - ͠xi*λ = -͠xi*

Это позволяет оценить новый max функции полезности, который получается при относительно малом изменении цены:

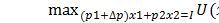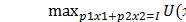= - ͠xi*λ*∆p

ЗАДАЧА МИНИМИЗАЦИИ РАСХОДОВ

Как достичь данного уровня полезности с минимальными расходами? Допустимое множество двойственной задачи выглядит как множество таких наборов из потребительского множества Х, полезность которых не меньше, чем u̅.

Аналитическая форма:

P1x1 + p2x2 = I → min

U (x1,x2) ≥ u̅

X1≥0, x2 ≥ 0

Функция Лагранжа имеет вид:

L (x1,x2,λ) = p1x1 + p2x2 + λ(u - u̅(x1,x2))

x̅1 = H1 (p1,p2,u)

x̅2 = H2 (p1,p2,u)

Обозначим решение этой задачи через Н(p,u) и будем называть соответствующее отображение компенсированным спросом (спросом по Хиксу).

Внутреннее равновесие, так же как и в задаче максимизации полезности характеризуется равенством MRS между двумя благами и их относительными ценами.

Следует различать обычную (маршаллианскую) кривую спроса и кривую компенсированного спроса. Первая выражает зависимость между ценой и величиной спроса с учетом как эффекта замещения, так и эффекта дохода. Она строится при фиксированном номинальном доходе потребителя. Вторая выражает зависимость между ценой и величиной спроса с учетом только эффекта замещения. Она строится при фиксированном реальном доходе потребителя. Поскольку для нормальных товаров общий эффект изменения цены превышает эффект замещения, кривая компенсированного спроса по этим товарам всегда круче обычной кривой спроса (рис. 3.3а). Поскольку по товарам низшей категории общий эффект изменения цены меньше эффекта замещения, кривая компенсированного спроса по этим товарам более полога, чем маршаллианская кривая спроса (рис. 3.36). Поскольку эффект замещения изменяет объем спроса в направлении, обратном изменению цен, кривая компенсированного спроса всегда имеет отрицательный наклон, тогда как обычная кривая спроса может иметь положительный наклон в случае товара Гиффена.

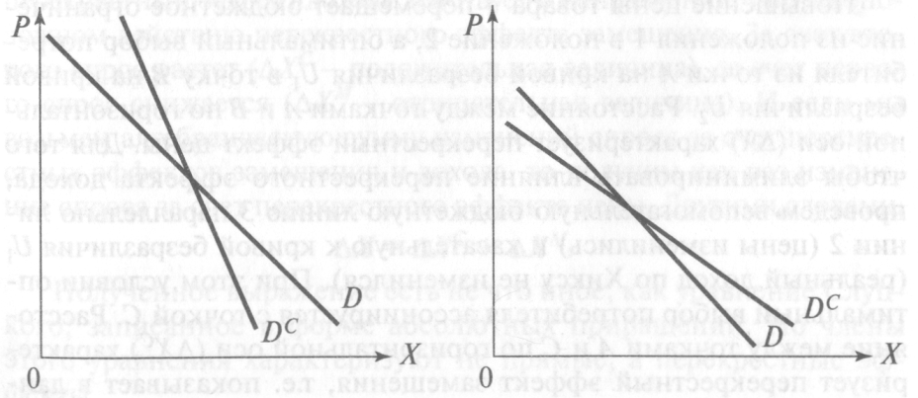
Рис. 3.3. Взаимное расположение маршаллианской кривой спроса (D^M) и кривой компенсированного спроса (D^C): а) для нормальных товаров; б) для товаров низшей категории

Свойства компенсированного спроса:

1. Однородность нулевой степени относительно цен: Н(λp,u̅) = Н(p,u̅) для любого λ.

2. Ограничение задачи минимизации расходов выполняется как равенство: для любого х*∊Н(p,u̅) имеем u(x*)= u̅.

3. Если предпочтения выпуклы, то множество Н(p,u̅) выпукло

4. Если предпочтения строго выпуклы, то множество Н(p,u̅) состоит из одного элемента, т.е. отображение является функцией компенсированного спроса

5. Имеет место закон компенсированного спроса: для любых х`∊ Н(p`,u̅) и x``∊ Н(p``,u̅) имеем: (p`-p``)(x`-x``)≤ 0

Изучив свойства решения задачи минимизации расходов обратим внимание на значение минимальных расходов. Подставив решение задачи в целевую функцию, мы получим зависимость уровня минимальных расходов от цен и уровня полезности. Полученную функцию отражающую эту зависимость называют функцией расходов:

e(p,u̅) = px*, где х ∊ Н(p,u̅)

Свойства функции расходов:

1. Данная функция не убывает по ценам:

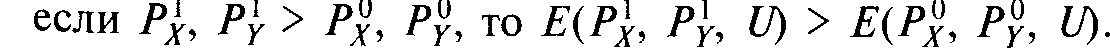
Если количества товаров в оптимальном потребительском наборе строго положительны, рост цены отдельного товара, как таковой, уменьшает максимально достижимый уровень полезноcти и для достижения потребителем исходного уровня полезности его расходы следует увеличить.

2. Функция расходов линейно однородна по ценам:

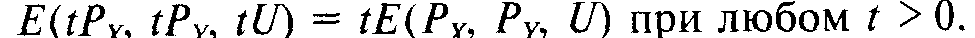
Если цены товаров растут в одинаковой пропорции, то расходы, требуемые для достижения данного целевого уровня полезности, следует увеличить в той же пропорции.

3. Возрастает по уровню полезности.

4.? Функция расходов вогнута по ценам, т.е. растет по цене убывающим темпом, что обусловлено замещением более дорогого товара более дешевыми в оптимальном наборе (т.е. наборе заданной полезности и минимальной стоимости) по мере подорожания одного из товаров.

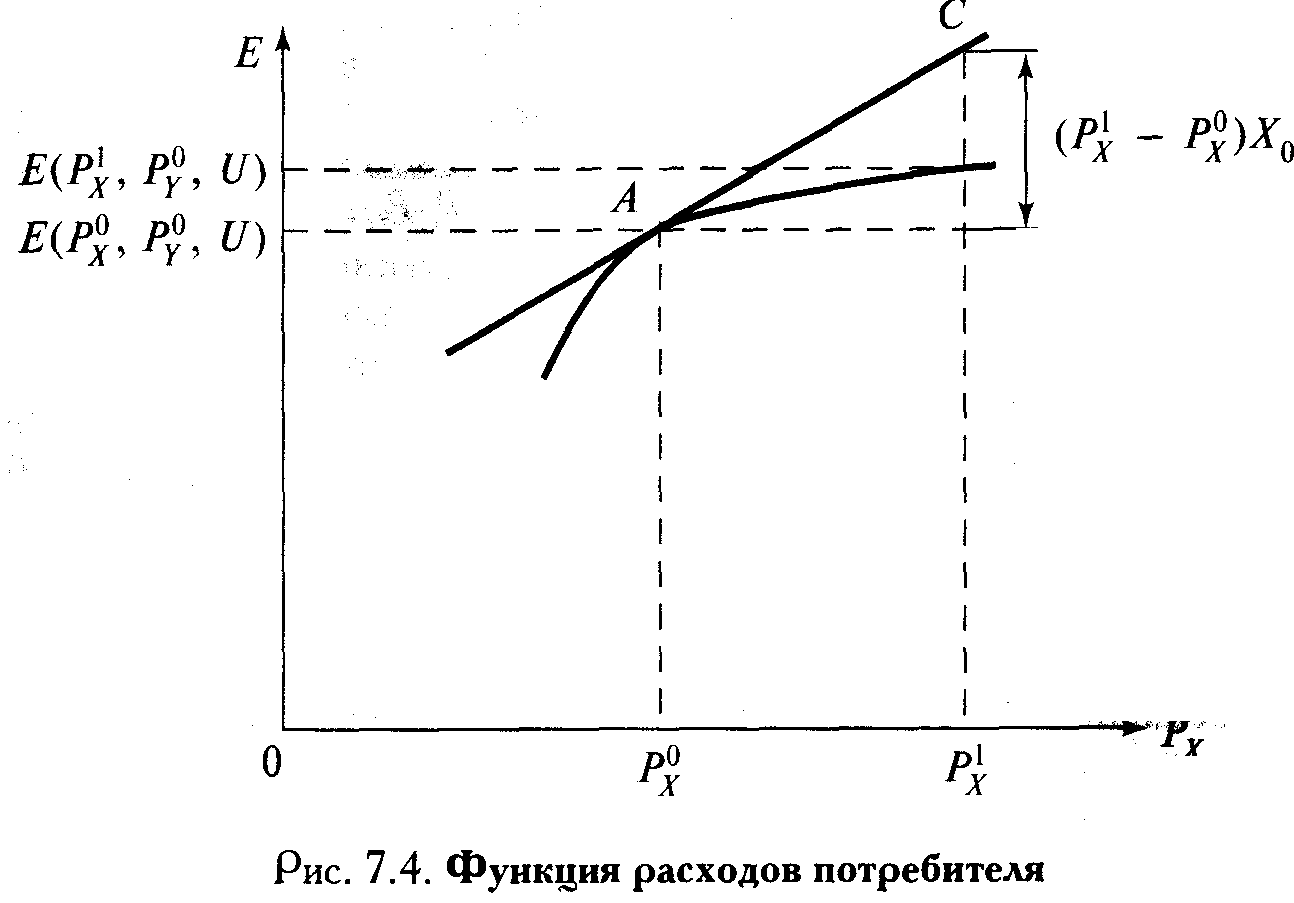
5.Функция расходов непрерывна по ценам, при принятии их значений положительными. Хотя свойство 4, вообще говоря, не вытекает с необходимостью из свойства 3, мы принимаем его как удобную техническую предпосылку, благодаря которой функция расходов оказывается дважды дифференцируемой по ценам. Это, в свою очередь, обеспечивает наличие у нее свойства 5.

6.Зная функцию расходов, можно относительно легко, т.е. не решая двойственную задачу, найти хиксианский спрос на товар. Достаточно применить лемму Шепарда, согласно которой этот спрос (для товара X) есть

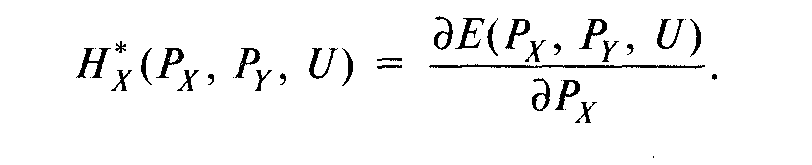
Доказательство:лемма Шепарда является закономерным результатом приведенного нами выше рассуждения, согласно которому график зависимости функции расходов от цены одного из товаров везде лежит либо под касательной к любой его точке, либо на ней. Если при этом, как мы уже предположили, частная производная функции расходов по цене товара существует при всех положительных значениях этой цены, т.е. изгиб кривой является гладким, то наклон в любой точке кривой, описывающей функцию расходов, есть не что иное, как оптимальный спрос индивида в этой точке, окажем это в общем виде, считая, что нам заданы вектор цен Р° и соответствующий ему минимизирующий расходы потребителя товарный набор q°. Тогда, по определению,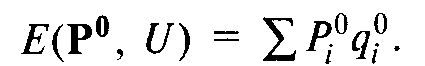

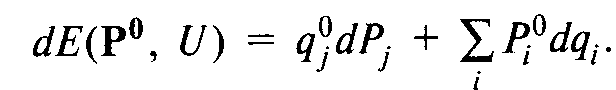
Поскольку мы приняли полезность неизменной, изменения dq_i должны удовлетворять следующему условию: 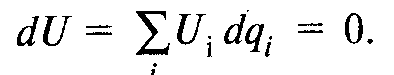Но из условия первого порядка задачи минимизации расходов следует, что 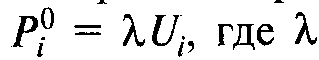— это величина, обратная предельной полезности дохода. Поэтому мы имеем:

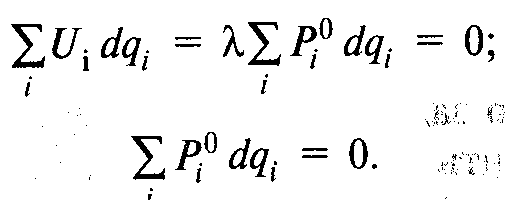
Следовательно, хотя потребитель, как правило, изменяет структуру своего потребления в ответ на малое изменение цены, такая корректировка оказывает незначительное влияние на минимальные расходы, требуемые для достижения данной целевой полезности, и потому, при неизменности цен остальных товаров и полезности, равенство принимает вид: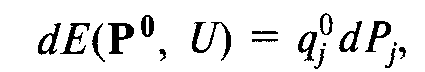

Откуда следует, что количество товара qf равно частной производной функции расходов по цене данного товара в точке исходного выбора. Поскольку данная частная производная есть функция от Р° и U, это количество товара qj также выступает функцией указанных переменных и потому есть функция компенсированного (хиксианского) спроса на данный товар: