Метод анализа экспертных мнений с помощью дерева решений

В процессе подготовки решения выделяют различные его варианты, которые могут быть приняты, а также для каждого из вариантов - ситуации, которые могут наступить независимо от воли принимающего решение. Эти ситуации также принимают во внимание.

Далее, изображая графически возможные варианты решений и их последствия, получают дерево решений, которое в зависимости от степени сложности проблемы имеет различное число ветвей.

Следуя от исходной точки вдоль ветвей дерева, можно различными путями достичь любой его конечной точки. Ветвям конкретного дерева соотносят объективные или субъективные оценки возможности реализации рассматриваемых событий и влияния на них принимаемых решений или выполняемых действий (достоверность, размеры затрат и доходов). Таким образом, следуя вдоль ветвей дерева, возможно с помощью известных правил комбинирования оценок оценить каждый вариант пути так, что они станут практически сравнимыми для лица принимающего решения (ЛПР). Следовательно, возможно найти оптимальные решения и одновременно возможно проранжировать различные способы действий.

Для оценки используют вероятности, коэффициенты уверенности или шансы. Комбинирование оценок ведут с помощью правил логического вывода в условиях неполной определенности.

Рассмотрим пример, когда для оценки используют вероятности. В этом случае для их комбинирования используют Байесов подход. Согласно ему степень неопределенности каждого события оценивается вероятностью
«0-1». Исходными данными для применения метода Байеса служат не только вероятности, но и коэффициенты уверенности, а также шансы, на основании которых вычисляются вероятности.

Байесов подход позволяет определять относительное правдоподобие заключений в зависимости от наличия или отсутствия подтверждающих или отрицающих их свидетельств. Он основан на теореме Байеса:

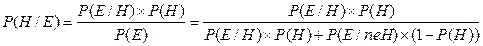(14)

где 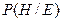- апостериорная вероятность заключения 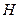при наличии свидетельства 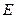(т. е. вероятность заключения 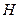при условии, что известен факт существования );

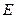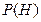- априорная вероятность заключения 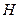при отсутствии каких-либо свидетельств;

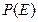- вероятность свидетельства ;

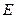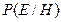- вероятность того, что свидетельство 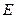имеет место, если истинно заключение ;

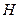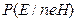- вероятность того, что свидетельство 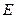имеет место, если заключение 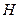ложно.

Согласно 14, получение новых независимых свидетельств позволяет увеличить или уменьшить вероятность заключения. При этом учет свидетельства с номером 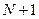проводится на базе вероятности, вычисленной с учетом 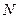предыдущих свидетельств.

Задание №2.

Главный экономист предприятия (ЛПР) анализирует планы развития производства на следующий год. Предприятие выпускает, помимо прочего, изделие 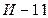. Его выпускают в течение длительного срока и реализуют потребителям без всяких затруднений. В плане развития предусматривается перейти к выпуску более современных изделий, чем 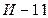. Предлагается два варианта новых моделе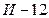й: и 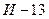. Из них последняя является более современной.

Предварительные расчеты показывают, что переход на выпуск модели 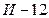принесет за год чистой прибыли на 20 млн. больше, чем выпуск 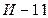(в случае, если реализация новой модели будет удачной). Если реализация новой модели будет идти с затруднениями, то ее производство снизит годовую прибыль на 2 млн. Аналогичные расчеты, произведенные по модели 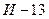, дали такие результаты: при удачном исходе - увеличение прибыли на 30 млн., при неудачном исходе - уменьшение прибыли на 15 млн.

Исходя из знания производственных условий предприятия и рыночной ситуации, ЛПР уверено в успехе на 70%.

ЛПР известно, что существует маркетинговая организация, которая занимается исследованиями в области прогнозирования ситуаций, связанных с модернизацией продукции и выводом ее на рынок. Подобное исследование для данного предприятия будет стоить 300 тыс. Из прошлого опыта известно, что заключения данной организации оказывались верными в 60% случаев, когда предсказывался успех, и в 80% случаев, когда предсказывалась неудача.

Нужно принять решения:

- стоит ли обращаться к услугам маркетингового агентства?

- переходить ли на выпуск нового изделия или продолжать выпускать старую?

- если переходить, то какую модель предпочесть?

Данная задача довольно сложная, поскольку имеется несколько возможных вариантов принятия решений, а также много неупорядоченной информации, вероятностного характера.

Решение.

Для решения подобного рода задач строят дерево решений, которое помогает точно сформулировать проблему и организовать поиск оптимального решения.

Дерево решений, построенное для условий рассматриваемого примера, представлено на рис.1. На рисунке приняты следующие условные обозначения:

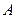- - начальное состояние;

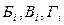- - состояния или точки ветвления;

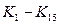- - конечные состояния;

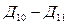- - действия первого уровня;

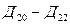- - действия второго уровня;

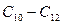- - события первого уровня;

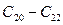- - события второго уровня .

Анализируя дерево процедуры принятия решений, несложно заметить, что оно включает ветви двух видов:

- действия, которые зависят от решения ЛПР (закажет оно анализ или нет, какие модели изделия будет рекомендовать к выпуску в следующем году);

- события, которые являются последствиями решений ЛПР, однако на характер которых он не может повлиять (после принятия решения о выпуске нового изделия, успех или неудача с его реализацией не зависят от ЛПР, нельзя также повлиять на характер заключения маркетингового агентства).

На рис. 1 показаны все возможные действия и их последствия, т.е. логическая структура задачи.

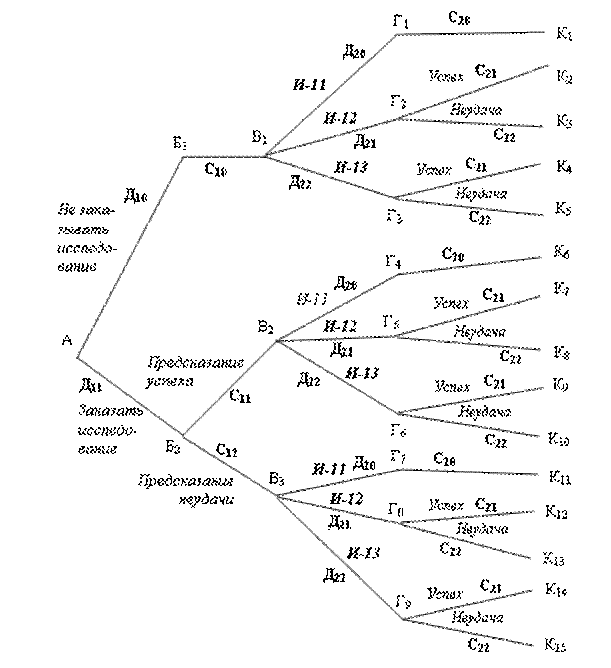
Рис.1. Логическая структура задачи

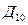- действия, заключающиеся в том, что исследования заказаны не будут.

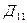- действия, заключающиеся в заказе исследований маркетинговому агентству.

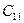- события, заключающиеся в предсказании успеха.

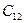- события, заключающиеся в предсказании неудачи.

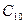- фиктивное событие, введенное для выравнивания числа ветвей.

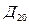- действия заключающиеся в продолжении выпуска изделия .

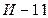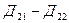- действия, заключающиеся в переходе, соответственно, на модель 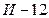и .

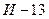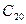- событие, заключающееся в рыночном успехе продолжения выпуска изделия .

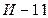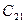- событие, заключающееся в успехе перехода на выпуск одной из новых моделей.

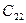- событие, заключающееся в неудаче перехода на выпуск одной из новых моделей.

Однако на основании данного дерева мы не можем сказать, какое из возможных решений будет более рациональным. Для этого требуется дополнить дерево числовыми данными рис.2.

В приведенных выше данных имеются только сравнительные данные. Например, при успешном переходе на выпуск модели 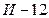дополнительная прибыль составит 20 млн. в год. Рассчитаем изменения в размерах прибыли на основании имеющихся в нашем распоряжении данных:

- «0» - если продолжать выпуск изделия ;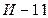

- «+20» - если перейти на выпуск модели 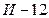и она получит успех на рынке;

- «-2» - если модель 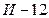будет не востребована потребителями;

- «+30» - если осуществится успешный переход на выпуск модели ;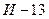

- «-15» - если переход на выпуск модели 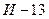будет неудачным.

Известно также, что исследование маркетингового агентства обойдется в 300 тыс. Результаты подсчета алгебраических сумм этих величин записаны справа от вершин дерева на рис. 2.

Теперь, оценить различные варианты действий. Из рисунка видно, что переход на выпуск изделий 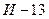по сравнению с переходом на выпуск изделий 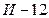является более рискованным. Однако, с другой стороны, модель 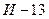дает большую прибыль, чем модель 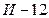. А может быть целесообразнее продолжать выпускать изделие 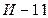? При получении ответа на эти вопросы следует учесть вероятности.

Данная задача решалась бы весьма просто, если было бы точно известно, какое из событи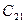й или 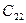произойдет. Однако это неизвестно. В условиях задачи говорится, что ЛПР на 70% уверено в успехе перехода на выпуск одной из новых моделей изделия. То есть вероятность благоприятного исхода в этом случае 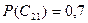. Поскольку 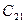и 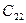составляют полную систему событий, то .

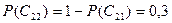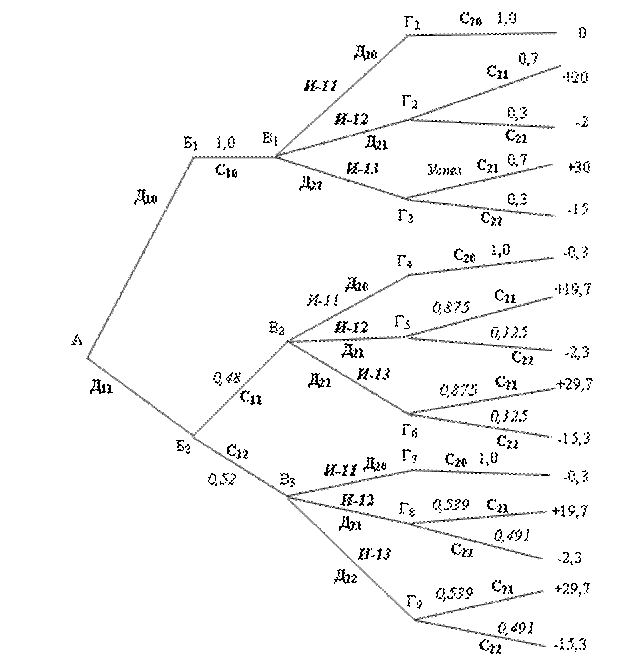
Рис. 2. Схема алгоритма решения

Эти субъективные вероятности, известные до принятия решения, являются априорными. Если ЛПР закажет исследование маркетинговому агентству, то оно учтет его результаты в своем заключении, т. е. первоначальные вероятност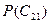и и 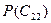будут уточнены. То есть будет внесена поправка, учитывающая как характер прогноза (предсказания) маркетингового агентства, так и его точность. Это можно оценить вполне объективно, поскольку известно, насколько прогнозы аналитиков оправдывались, когда они прогнозировали успешный исход, и насколько, когда они прогнозировали неудачу.

Исходя из имеющихся статистических данных, действительно успешное выведение новых товаров на рынок теми производителями, которые заказывали маркетинговое исследование, в 60% случаев предварительно предсказывалось маркетинговым агентством. Или вероятность того, что свидетельство подтверждающее успех имело место при успешном выведении нового товара на рынок 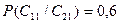. А так как 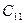(свидетельство, подтверждающее успех) и 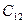(свидетельство, подтверждающее неудачу) составляют полную систему событий, то следует, что .

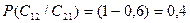Аналогичным образом, вероятность того, что свидетельство подтверждающее неудачу имело место при провале (неудаче) выведения нового товара на рынок 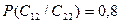. И соответственно .

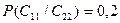Эти данные будут влиять на первоначальные субъективные оценки.

Эти и заданные в условиях вероятности показаны на рис. 2 (прямой шрифт). При этом вероятности фиктивных событий принимаем равными 1,0, т.е. 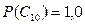и 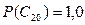(чтобы не влиять на результаты расчетов).

Получению заключений маркетингового агентства на дереве решений рис. 2 соответствуют действие 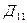и события 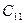или .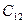

Рассчитаем апостериорные вероятности событи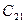й и 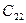с учетом результатов заключений маркетингового агентства ( 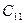и ).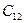

Для расчетов используем вторую форму записи формулы Байеса 14.

Вероятность успеха при предсказании успеха:

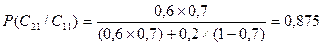(15).

Вероятность неудачи при предсказании успеха:

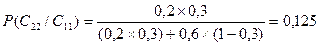(16).

Вероятность успеха при предсказании неудачи:

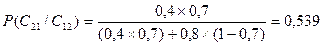(17).

Вероятность неудачи при предсказании неудачи:

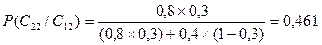(18).

Далее рассчитаем вероятности предсказания успеха и неудач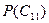и и 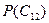. Для этого разрешим уравнение Байеса (первую форму записи, см. уравнение 14) относительно :

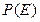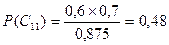(19).

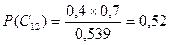(20).

Обозначим вычисленные вероятности на соответствующих ветвях дерева решений на рис. 2 (показано курсивом).

Алгоритм нахождения оптимального решения имеет следующий вид:

1. Для каждого состояния 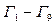(см. рис.1) вычисляем значения ожидаемых величин: ; ; ; ; ; ; ; ; .

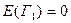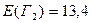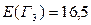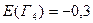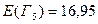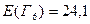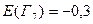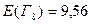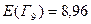Пример расчета для : .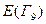

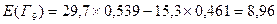2. Для каждого состояния 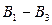(см. рис. 1) выберем ветвь 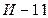, 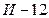или 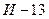, к которой относится максимальный ожидаемый прирост прибыли: ; ; .

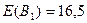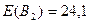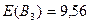3. В каждом состоянии 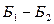(см. рис. 1) вычислим максимальный ожидаемый прирост прибыли: ; .

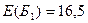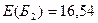4. Находясь в исходном состоянии 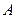, выберем такую ветвь, к которой относится максимальный ожидаемый результат.

Таким образом, опираясь на результаты приведенного выше анализа, оптимальная стратегия поведения главного экономиста выглядит следующим образом.

Заказать исследование аналитикам и если:

- заключение благоприятно, то принять решение о выпуске модели ;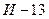

- неблагоприятно, то принять решение о выпуске модели 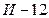.