Решить задачу линейного программирования симплекс-методом.

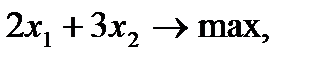
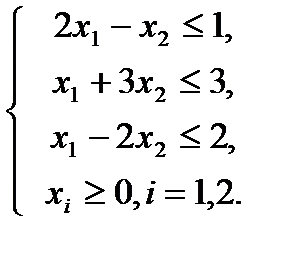
Решение.

Перед применением симплекс-метода необходимо преобразовать систему линейных ограничений и рассматриваемую нами функцию к каноническому виду.

Все свободные члены системы ограничений неотрицательны, значит, выполнено одно из необходимых условий применения симплекс-метода. Осталось все условия системы представить в виде уравнений. Для этого к левой части 1-го неравенства системы ограничений прибавляем неотрицательную переменную 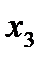, к левой части 2-го неравенства прибавляем неотрицательную переменную 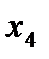, а к левой части 3-го - неотрицательную переменную , тем самым мы преобразуем неравенства в равенства:

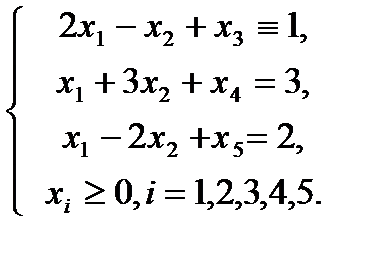
Определимся с начальным опорным решением. Наличие единичного базиса в системе ограничений позволяет легко найти его.

Переменная 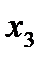входит в уравнение 1 с коэффициентом 1, а в остальные уравнения системы с коэффициентом 0, т.е. 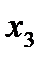- базисная переменная. Аналогично переменные 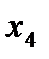и являются базисными. Остальные переменные являются свободными. Приравняв свободные переменные к 0 в системе ограничений, получаем опорное решение:

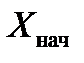= ( 0 , 0 , 1 , 3 , 2 ).

Теперь непосредственно составим таблицу:

Базисные Переменные		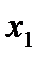		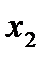		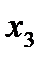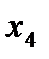Свободные переменные	Отношение
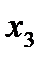		-1					-
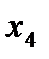		-2					-
J(x)	-2	-3					-

В качестве ведущего выступает 2-ой столбец, поскольку -3 - наименьший элемент в строке J(x). За ведущую строку принимаем строку 2, т. к. отношение свободного члена к соответствующему элементу выбранного столбца для 2-ой строки является наименьшим из неотрицательных. Разделим элементы 2-ой строки на 3, чтобы получить в качестве ведущего элемента 1:

Базисные Переменные		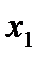		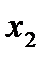		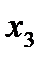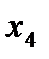Свободные переменные	Отношение
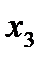		-1					-
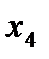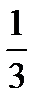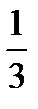		-2					-
J(x)	-2	-3					-

Взяв за ведущий выделенный элемент, проведем соответствующие преобразования.

От элементов строки 1 отнимаем соответствующие элементы строки 2, умноженные на -1.

От элементов строки 3 отнимаем соответствующие элементы строки 2, умноженные на -2.

От элементов строки J(x) отнимаем соответствующие элементы строки 2, умноженные на -3. В результате имеем:

Базисные Переменные		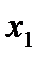		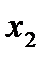		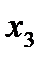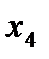Свободные переменные	Отношение
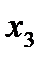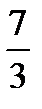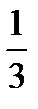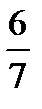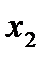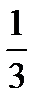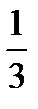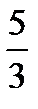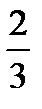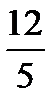J(x)	-						-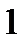

За ведущий столбец выберем столбец 1 ( по тому же правилу) , а за ведущую строку - строку 1. Разделим элементы 1-ой строки на :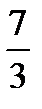

Базисные Переменные		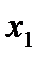		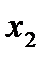		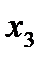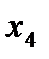Свободные переменные	Отношение
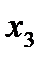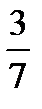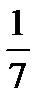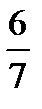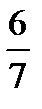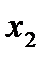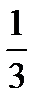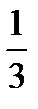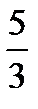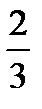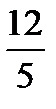J(x)	-1						-

Взяв за ведущий выделенный элемент, проведем соответствующие преобразования.

От элементов строки 2 отнимаем соответствующие элементы строки 1, умноженные на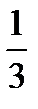

От элементов строки 3 отнимаем соответствующие элементы строки 1, умноженные на .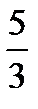

От элементов строки J(x) отнимаем соответствующие элементы строки 1, умноженные на -1. В результате имеем:

Базисные Переменные		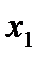		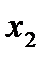		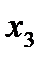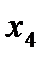Свободные члены	Отношение
							-
			-				-
			-				-
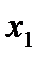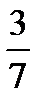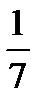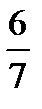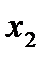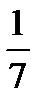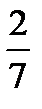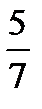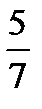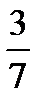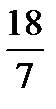J(x)							-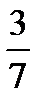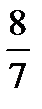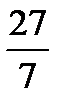

Мы получили строку J(x), состоящую только из неотрицательных элементов. Значит, оптимальное решение найдено, 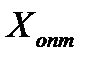= ( 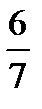, , 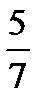0 , 0 , ).

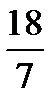J(x) = - -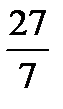

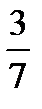
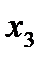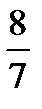
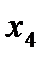
Поскольку 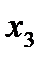и 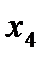по условию неотрицательны, наибольшее значение функции равно свободному члену, т. е. .

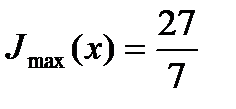Задача № 6.

Решить транспортную задачу.

Транспортная таблица имеет вид:

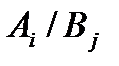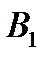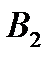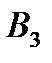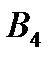					Запасы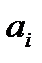
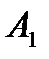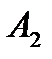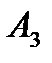Заявки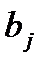

Решение.

Найдём общую сумму запасов: 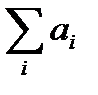= 70 + 70 + 110 = 250.

Найдём общую сумму заявок: 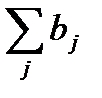=70 + 90 + 70 + 60 = 290.

В нашем случае запасы поставщиков ( 250 единиц продукции ) меньше, чем потребность потребителей ( 290 единиц продукции ) на 40 единиц. Введем в рассмотрение фиктивного поставщика 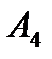с запасом продукции, равным 40. Стоимость доставки единицы продукции от данного поставщика ко всем потребителям примем равной нулю.

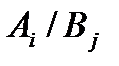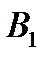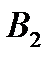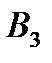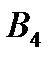					Запасы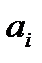
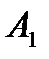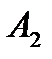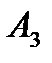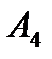Заявки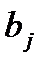

Решение транспортной задачи начнем с построения допустимого базисного плана, для этого воспользуемся методом северо-западного угла.

Рассмотрим ячейку 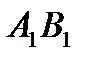таблицы. Запасы поставщика 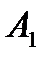составляют 70 единиц продукции, заявки потребителя 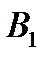составляет 70. Разместим в ячейку 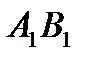значение , равное min { 70 , 70 } = 70, т.е. мы полностью израсходoвали запасы поставщика 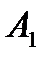. Вычеркиваем строку 1 таблицы, т.е исключаем ее из дальнейшего рассмотрения. В то же время мы полностью удовлетворили потребность потребителя 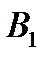, но будем считать, что потребность данного потребителя составляют 0 единиц продукции (не будем одновременно вычеркивать строку и столбец).

Рассмотрим ячейку 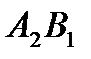.Запасы поставщика 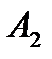составляют 70 единиц продукции. Потребность потребителя 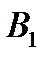составляет 0. Разместим в ячейку 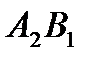значение, равное min { 70 , 0 } = 0 ,т.е. мы полностью удовлетворили потребность потребителя 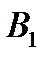. Поэтому исключаем 1ый столбец таблицы из дальнейшего рассмотрения.

Рассмотрим ячейку 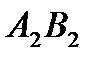.Запасы поставщика 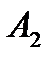составляют 70 единиц продукции. Потребность потребителя 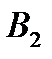составляет 90. Разместим в ячейку 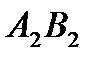значение, равное min { 70 , 90 } = 70 ,т.е. мы полностью израсходoвали запасы поставщика 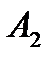. Вычеркиваем строку 2 таблицы, т.е исключаем ее из дальнейшего рассмотрения.

Рассмотрим ячейку 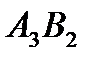.Запасы поставщика 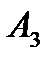составляют 110 единиц продукции. Потребность потребителя 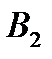составляет 90 – 70 = 20 . Разместим в ячейку 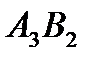значение, равное min { 110 , 20 } = 20 ,т.е. мы полностью удовлетворили запросы потребителя 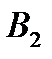. Поэтому исключаем 2ой столбец таблицы из дальнейшего рассмотрения.

Рассмотрим ячейку 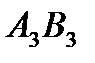.Запасы поставщика 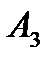составляют 110 – 20 = 90 единиц продукции. Потребность потребителя 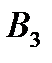составляет 70. Разместим в ячейку 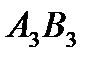значение, равное min { 90 , 70 } = 70 , т.е. мы полностью удовлетворили запросы потребителя 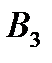. Поэтому исключаем 3ий столбец таблицы из дальнейшего рассмотрения.

Рассмотрим ячейку 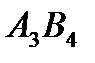. Запасы поставщика 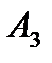составляют 90 – 70 = 20 единиц продукции. Потребность потребителя 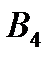составляет 60 . Разместим в ячейку 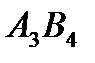значение, равное min { 20 , 60 } = 20 ,т.е. мы полностью израсходoвали запасы поставщика 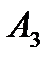. Поэтому исключаем 3ью строку таблицы из дальнейшего рассмотрения.

Рассмотрим ячейку 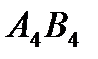. Запасы поставщика 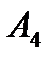составляют 40 единиц продукции. Потребность потребителя 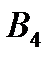составляет 60 – 20 = 40 . Разместим в ячейку 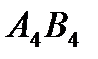значение, равное min { 40 , 40 } = 40 ,т.е. мы полностью израсходoвали запасы поставщика 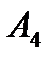. Поэтому исключаем 4ую строку таблицы из дальнейшего рассмотрения. В то же время мы полностью удовлетворили запросы потребителя .

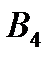Мы нашли начальное опорное решение, т.е. израсходовали все запасы поставщиков и удовлетворили все заявки потребителей. Занесем полученные значения в таблицу:

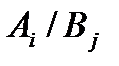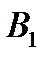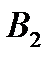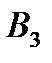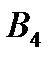					Запасы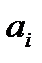
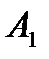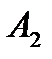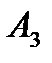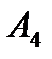Заявки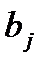

Теперь, произведем его оценку. Общие затраты на доставку всей продукции, для данного решения , составляют

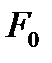= 20 70 + 15 0 + 9 70 + 19 20 + 15 70 + 13 20 + 0 40 = 3720 единиц.

Найдем потенциалы поставщиков 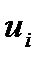и потребителей 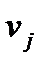. Примем 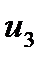= 0. Тогда :

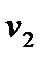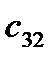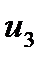= - = 19 - 0 = 19

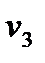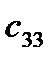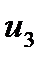= - = 15 - 0 = 15

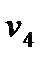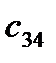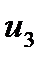= - = 13 - 0 = 13

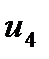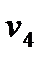= - = 0 - 13 = -13

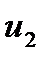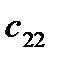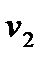= - = 9 - 19 = -10

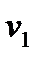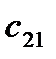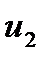= - = 15 – ( -10 ) = 25

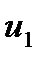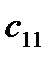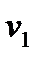= - = 20 - 25 = -5

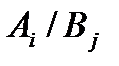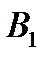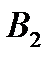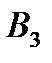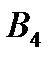					Запасы	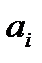Потенциалы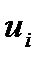
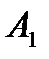						-5
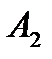						-10
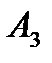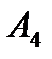						-13
Заявки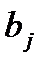
Потенциалы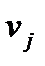

Найдем оценки свободных ячеек следующим образом :

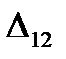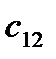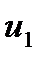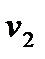= - ( + ) = 13 - ( -5 + 19 ) = -1

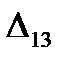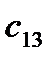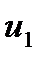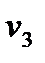= - ( + ) = 8 - ( -5 + 15 ) = -2

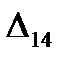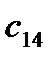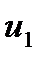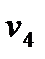= - ( + ) = 11 - ( -5 + 13 ) = 3

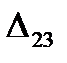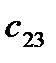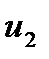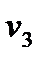= - ( + ) = 17 - ( -10 + 15 ) = 12

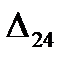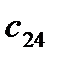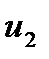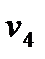= - ( + ) = 18 - ( -10 + 13 ) = 15

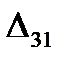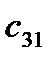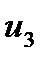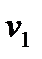= - ( + ) = 21 - ( 0 + 25 ) = -4

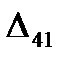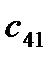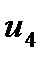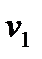= - ( + ) = 0 - ( -13 + 25 ) = -12

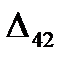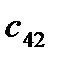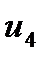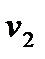= - ( + ) = 0 - ( -13 + 19 ) = -6

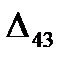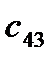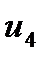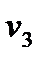= - ( + ) = 0 - ( -13 + 15 ) = -2

Среди оценок есть отрицательные, следовательно, решение не оптимальное.

Из отрицательных оценок выбираем минимальную, она соответствует ячейке 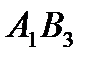, ее оценка 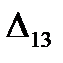= -2.

Ячейки 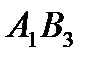, , 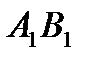, , 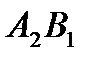, 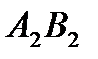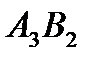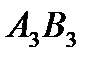образуют цикл для свободной ячейки 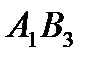. Цикл начинается в этой свободной ячейке. Пусть ячейка 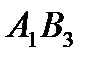имеет порядковый номер 1.

Среди ячеек цикла 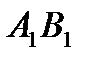, , 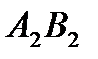, 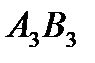номера которых четные , выберем ячейку 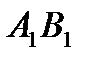, как обладающую наименьшим значением 70. От ячеек цикла с четными номерами, мы отнимаем 70. К ячейкам с нечетными номерами мы прибавляем 70. Ячейка 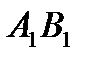выйдет из базиса, ячейка 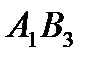станет базисной.

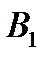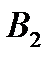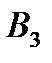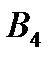					Запасы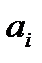
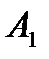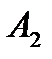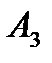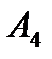Заявки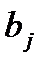

Общие затраты на доставку всей продукции, для данного решения , составляют

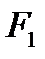= 8 70 + 15 70 + 19 90 + 13 20 + 0 40 = 3580 единиц.

Найдем потенциалы поставщиков 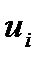и потребителей 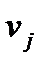. Примем 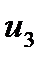= 0. Тогда :

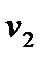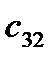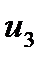= - = 19 - 0 = 19

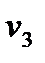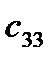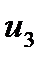= - = 15 - 0 = 15

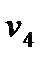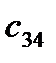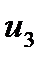= - = 13 - 0 = 13

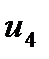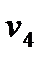= - = 0 - 13 = -13

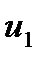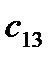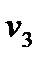= - = 8 - 15 = -7

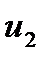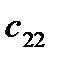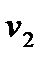= - = 9 - 19 = -10

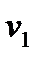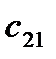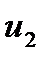= - = 15 – ( -10 ) = 25

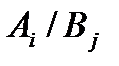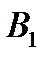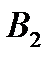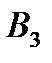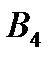					Запасы	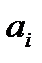Потенциалы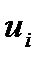
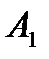						-7
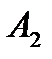						-10
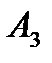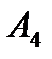						-13
Заявки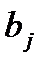
Потенциалы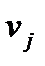

Найдем оценки свободных ячеек следующим образом :

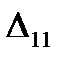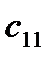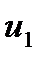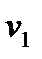= - ( + ) = 20 - ( -7 + 25 ) = 2

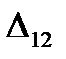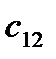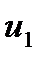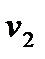= - ( + ) = 13 - ( -7 + 19 ) = 1

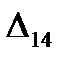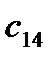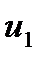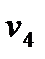= - ( + ) = 11 - ( -7 + 13 ) = 5

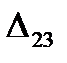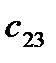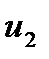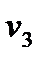= - ( + ) = 17 - ( -10 + 15 ) = 12

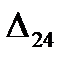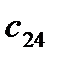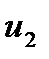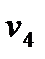= - ( + ) = 18 - ( -10 + 13 ) = 15

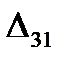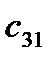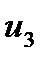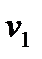= - ( + ) = 21 - ( 0 + 25 ) = -4

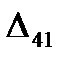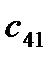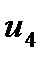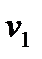= - ( + ) = 0 - ( -13 + 25 ) = -12

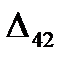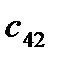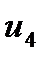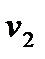= - ( + ) = 0 - ( -13 + 19 ) = -6

Среди оценок есть отрицательные, следовательно, решение не оптимальное.

Из отрицательных оценок выбираем минимальную, она соответствует ячейке 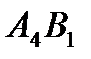, ее оценка 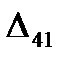= -12.

Ячейки 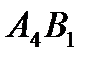, , 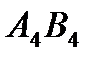, , 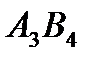, 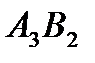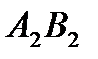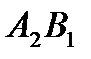образуют цикл для свободной ячейки 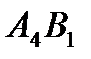. Цикл начинается в этой свободной ячейке. Пусть ячейка 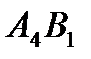имеет порядковый номер 1.

Среди ячеек цикла 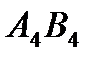, , 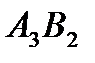, 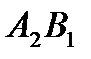номера которых четные , выберем ячейку 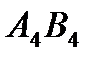, как обладающую наименьшим значением 40. От ячеек цикла с четными номерами, мы отнимаем 40. К ячейкам с нечетными номерами мы прибавляем 40. Ячейка 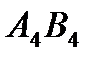выйдет из базиса, ячейка 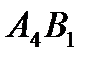станет базисной.

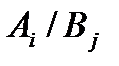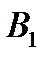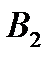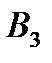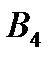					Запасы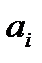
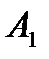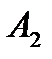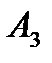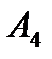Заявки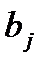

Общие затраты на доставку всей продукции, для данного решения , составляют

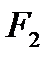= 8 70 + 15 30 + 9 40 + 19 50 + 13 60 + 0 40 = 3100 единиц.

Найдем потенциалы поставщиков 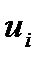и потребителей 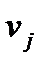. Примем 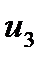= 0. Тогда :

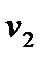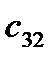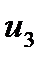= - = 19 - 0 = 19

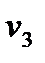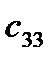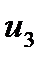= - = 15 - 0 = 15

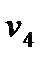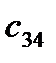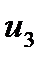= - = 13 - 0 = 13

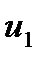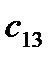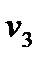= - = 8 - 15 = -7

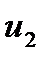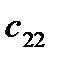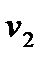= - = 9 - 19 = -10

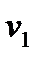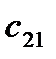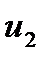= - = 15 – ( -10 ) = 25

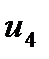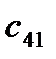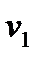= - = 0 - 25 = -25

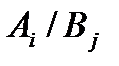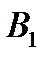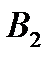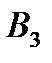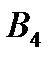					Запасы	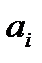Потенциалы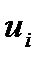
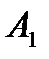						-7
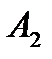						-10
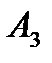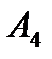						-25
Заявки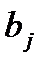
Потенциалы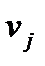

Найдем оценки свободных ячеек следующим образом :

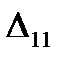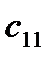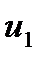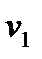= - ( + ) = 20 - ( -7 + 25 ) = 2

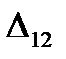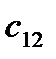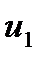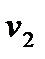= - ( + ) = 13 - ( -7 + 19 ) = 1

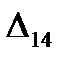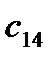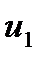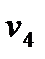= - ( + ) = 11 - ( -7 + 13 ) = 5

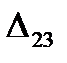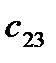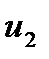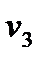= - ( + ) = 17 - ( -10 + 15 ) = 12

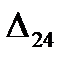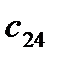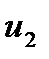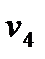= - ( + ) = 18 - ( -10 + 13 ) = 15

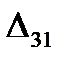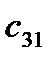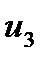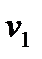= - ( + ) = 21 - ( 0 + 25 ) = -4

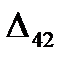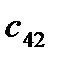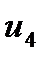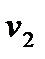= - ( + ) = 0 - ( -25 + 19 ) = 6

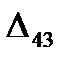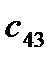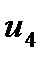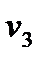= - ( + ) = 0 - ( -25 + 15 ) = 10

= - (
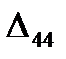