Построение кривой оперативной характеристики (ОХ) по распределению Пуассона
С помощью таблицы распределения Пуассона (табл П2) легко показать, что при одних и тех же объемах выборки n и числе r (отслеживаемых в ней дефектных изделий) вероятность появления дефектных изделий хорошо отображает дефектность партий, из которых берется выборка. Действительно, из сильно засоренных партий, где P = 6%, вероятность появления трех и более дефектных изделий P(r³) » 0,94, а из партии, где P = 0,8%, только 0,05. Следовательно, по вероятности появления в выборке одного и того же объема (в данном случае n = 100) какого-то числа дефектных изделий (в данном случае трех и больше) можно оценить дефектность партий, из которых брались выборки (в данном случае 6 и 0,8%). Если же подобными расчетами охватить больший диапазон дефектности партий, а расчеты провести не для двух «засоренностей», а, например, для десяти, то можно оценить дефектность партий по вероятности присутствия в выборках из них более чем какого-то определенного количества дефектных изделий. Такую зависимость, отображенную графически, называют оперативной характеристикой (ОХ).
Для построения кривой ОХ можно решать уравнение Пуассона:
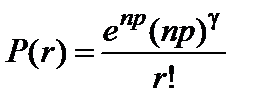 ,
,
, где вероятность P(r) наличия дефектных изделий в выборке объемом n ровно r и больше, когда в ней ожидается np дефектных изделий. На практике, однако, для построения ОХ удобнее пользоваться таблицей распределения Пуассона (см. табл.П2).
Таблицы Пуассона и биноминального распределения (см. табл.П1) непосредственно не содержат вероятностей «r и меньше», которые могут быть легко найдены из этих таблиц вычетом из 1 «хвоста распределения» от значения «r + 1 и больше». Полученные таким образом данные по зависимости вероятности Pa приемки партий от их дефектности р, являются основой для построения ОХ (рис 1.1
Зависимость вероятности Pa приемки партий от их дефектности P, оцениваемая по количеству дефектных изделий r ≤ 3 в выборке объемом n = 150
|
 Рис.1.1. Кривая ОХ для объема выборки n = 150 и приемочного числа Ac = 3 Рис.1.1. Кривая ОХ для объема выборки n = 150 и приемочного числа Ac = 3 |
).
Рис.1.1. Кривая ОХ для объема выборки n = 150 и Ac = 3
Л1 - б) Оперативная характеристика ВК по альтернативному признаку. AQL-контроль, понятия приемлемого уровня AQL дефектности, α -и β рисках, среднего выходного качества AOQ и его предела AOQL
1.4 Понятия α -и β риска при AQL-ВК
Договоренности поставщиков и потребителей в отношении схемы выборочного контроля основываются на их компромиссе относительно рисков α и β соответственно забракования партий так называемого приемлемого уровня AQL дефектности (риск α для дефектности партий p1 ≤ AQL) и риска пропуска через контроль партии заведомо неприемлемого уровня дефектности (риск β для дефектности партии p2 ≥ LQ).
Таким образом, задача определения компромиссной схемы выборочного контроля сводится к отысканию такой его оперативной характеристики, которая пройдет через точки (p1 = AQL, α) и (p2 = LQ, β), называемые соответственно точками риска поставщика и потребителя. На практике, однако, чаще используют стандартные значения рисков поставщика α, равные 0,05 или 0,01, и стандартные значения рисков потребителя β, равные 0,01; 0,05 или 0,10. Для этих стандартных сочетаний разработан экспрессный метод построения ОХ с помощью двух таблиц Камерона (табл.П3 и П4).
Первая таблица Камерона (см. табл.П3) позволяет на основании координат риска поставщика (p1, α) и потребителя (p2, β) определить объем выборки n и приемочное число Aс контроля. Эта таблица отношений p2/p1 соответствует двум группам сочетаний a и b: первые пять столбцов слева соответствуют группе с a= 0,05; следующие пять столбцов образуют группу с b= 0,01. Каждая из этих групп развертывается по значениям a = 0,1; 0,05 и 0,01.Вторая таблица Камерона (см. табл.П4) - это таблица значений m = np. Она позволяет построить ОХ по значению приемочного числа Ас. Полученная по координатам точек кривая ОХ приведена на рис.1.2.

Рис.1.2. Кривая ОХ выборочного плана для a = 0,05; b = 0,10; p1 = 2%; p2 = 8%, Ac = 4
