В. Методы расчета объема выборки.

На практике используются несколько подходов к определению объема выборки:

1. Произвольный метод расчета, основанный на применении «правила большого пальца», согласно которому бездоказательно принимается, что для получения точных результатов выборка должна составлять 5% от генеральной совокупности.

2. Традиционный метод расчета связан с проведением периодических ежегодных исследований с одним и тем же объемом выборки. К примеру, в социологических исследованиях (при изучении общественного мнения) выборка обычно составляет 1000–1200 человек /2, с. 220–221/. А при проведении маркетинговых исследований необходимый размер выборки можно приблизительно оценить, зная, в каких пределах он обычно находится (табл. 6) /1, с. 416/.

Таблица 6 – Минимальный и типичный размер выборки при проведении маркетинговых исследований

Тип исследования	Объем выборки
минимальный размер	типичный диапазон
Исследования в целях выявления проблемы (например, изучение рыночного потенциала)		1000–2500
Исследования в целях решения проблемы (например, разработка ценовой стратегии)		300–500
Тестирование товара		300–500
Маркетинговый тест (пробный маркетинг)		300–500
Исследования рекламы (в расчете на одно рекламное объявление, эффективность которого исследуется)		200–300
Аудит розничной торговли на пробном рынке	10 магазинов	10–20 магазинов
Проведение фокус-групп	6 групп	10–15 групп

3. Статистический метод расчета основан на определении статистической надежности информации. На его объем влияют следующие факторы:

– наличие сведений об объеме генеральной совокупности и степени ее однородности;

– требуемая точность результатов, регулируемая величиной максимально допустимой ошибки репрезентативности и величиной доверительной вероятности, с которой делается заключение о достоверности результатов исследования;

– наличие сведений о средних показателях генеральной совокупности по исследуемому признаку или об интервале варьирования признака (дисперсии);

– возможность повторного попадания единицы генеральной совокупности в выборку.

При определении объема выборки для больших совокупностей (когда объем выборки составляет менее 5%генеральной совокупности) могут использоваться следующие формулы:

а) повторная выборка (при возможности повторного попадания еди­ницы генеральной совокупности в выборку) при неизвестном объеме генеральной совокупности, но известном распределении контролиру­емого признака:

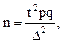(1)

где t – коэффициент доверия, зависящий от вероятности (p), с которой можно гарантировать, что предельная ошибка не превысит t-кратную среднюю ошибку (при доверительной вероятности р = 0,999 (99,9%), t = 3,28; р = 0,990 (99%), t = 3; p = 0,954 (95%), t = 1,96 ≈ 2);

p – найденная вариация генеральной совокупности, в процентах или в долях; q = 100 – p;

∆ – допустимая ошибка, в процентах или в долях;

б) повторная выборка при известной дисперсии изучаемого признака (σ):

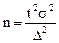; (2)

в) бесповторная выборка (при исключении возможности повторного попадания единицы генеральной совокупности в выборку) при известном объеме генеральной совокупности и известном распределении контролируемого признака:

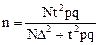, (3)

где N – объем генеральной совокупности;

г) бесповторная выборка при известной дисперсии изучаемого признака:

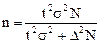, (4)

где t – коэффициент доверия, зависящий от вероятности (р), с которой можно гарантировать, что предельная ошибка не превысит t-кратную среднюю ошибку (при Р = 0,990 он равен 3; при Р = 0,999, t = 3,28; при Р = 0,954, t = 2). В маркетинговых исследованиях обычно используют коэффициент доверия
равный 2-м;

σ² – дисперсия изучаемого признака (ее обычно определяют на основе эксперимента, пробного обследования или же по аналогам);

∆ – предельная (заданная) ошибка выборки, которая обычно задается не более 30% (или 0,3);

N – число единиц в изучаемой (генеральной) совокупности /3, с. 120/;

д) выборка признается малой, если ее объем превышает 5% генеральной совокупности, в этом случае объем выборки может быть откорректирован:

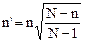, (5)

где n' – объем выборки для малой совокупности,

n – объем статистической выборки,

N – объем генеральной совокупности;

е) расчет статистической выборки при нормированном отклонении t= 2 и допустимой ошибке 5% (табл. 6) показывает, что для больших совокупностей объем выборки может быть определен любым способом, поскольку используемые практические приемы приводят скорее к завышению объема обследуемой совокупности.

Таблица 6 – Зависимость объема выборки (n)

от величины генеральной совокупности (N)*

Объем N									>
Объем n
* при нормированном отклонении t = 2 и допустимой ошибке 5%

Из таблицы 6 видно, что при размере генеральной совокупности более 5000 ее величина не влияет на размер выборки, поэтому формула может принять следующий вид (величиной 1/Nможно пренебречь):

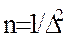. (6)

Таким образом, при отсутствии точной информации о размере и характеристиках генеральной совокупности (при условии, что она не менее 5000) достаточно включить в выборку 400 ее представителей;

д) количество респондентов, которых необходимо опросить для получения необходимого числа положительных ответов на интересующий вопрос, можно рассчитать по формуле:

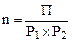, (7)

где П – требуемое для анализаколичество положительных ответов;

Р₁ – доля положительных ответов;

Р₂ – доля целевых групп, рассчитываемая как произведение всех долей респондентов, удовлетворяющих установленным требованиям (возраст, пол, статус пользователя и т.д.).

4. Метод расчета с помощью номограмм /4, с. 131–133/.

5. Эмпирический метод – в этом случае выборка считается достаточной, когда все новые сведения вносят лишь незначительные изменения (которыми можно пренебречь) в уже собранные результаты исследования.

6. Затратный метод – основан на размере расходов,
которые допустимо затратить на проведение исследования
/4, с. 128–131/.

Приведем пример разработки выборочного плана и определения объема выборки среди клиентов СКУ «Алма-Арасан», «Коктем» и «Турксиб», которые приобрели путевку на лечение и отдых в III квартале (так как этот период характеризуется наибольшей их заполняемостью клиентами, что предъявляет повышенные требования к деятельности персонала и к качеству оказываемых услуг) текущего года. Единицей выборки выступает клиент соответствующего СКУ, получающий санаторно-курортное лечение в этот же период, но проживающий в обычном номере. За рамку выборки был принят список зарегистрированных в СКУ клиентов в этом же периоде. Объем выборки был рассчитан на основе статистической формулы. В процессе исследования использовался вероятностный (случайный) метод выборки, то есть все единицы выборки имели одинаковый шанс быть включенными в выборку. Вероятностный метод основывался на систематическом отборе, при котором формирование выборки осуществлялось с помощью показателя «интервала скачка» (табл. 7).

Таблица 7 – Процесс формирования выборки для исследования степени
удовлетворенности клиентов СКУ качеством санаторно-курортных услуг

Наименование показателей	Характеристика показателей
Генеральная совокупность	Люди, которые приобрели путевку в СКУ на III квартал текущего года (5000 чел.)
Единица выборки	Клиент СКУ, получающий санаторно-курортное лечение и проживающий в обычном номере
Рамка выборки	Список клиентов, зарегистрированных в регистратуре СКУ на момент проведения опроса
Объем выборки	Был рассчитан по формуле и составил 120 человек
Метод выборки	вероятностный (случайный)
Тип метода выборки	Систематический отбор
Интервал скачка	Через 42 человека

Ставилась задача получить репрезентативные оценки в разрезе каждого санатория.

Основу проведенного анкетирования составил статистический метод выборочного наблюдения. Поэтому было проведено предварительное изучение генеральной совокупности (всех клиентов СКУ), оценка ее гомогенности (однородности) и определен необходимый объем выборки. Расчет объема выборки производился по формуле 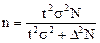/3, с. 120/. Согласно этой формуле известны коэффициент доверия (t), генеральная совокупность (N), предельная ошибка выборки (∆). Неизвестным остается лишь дисперсия изучаемого признака (σ²).

Она, как известно, вычисляется по формуле:

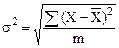, (8)

где х – балльная оценка, данная отдельным респондентом;

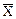– средняя балльная оценка, данная всеми респондентами;

m – количество вариантов ответов на вопрос.

Средняя балльная оценка рассчитывается по формуле:

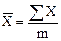. (9)

Пример расчета дисперсии изучаемого признака:

Расчет дисперсии, то есть разброс вариантов ответа респондента, может проводиться на основе результатов пилотного опроса, в котором могут быть опрошены 15–30 респондентов. Из анкеты выбираются несколько ключевых вопросов, по которым рассчитывается дисперсия. Затем по этим вопросам рассчитывается ее среднее значение. При этом чем шире размах ответов, тем большим будет объем выборки, то есть число респондентов, которых следует опросить. Для примера покажем, как рассчитывается дисперсия по одному вопросу:

Вопрос: «Когда был произведен первичный осмотр лечащим врачом?»
Количество ответов	Варианты ответов	Количество ответов по результатам пилотного опроса среди 15 респондентов
m = 5	□ в день прибытия (я прибыл(-а) утром)	Х1 = 7
□ на следующий день	Х2 = 4
□ на 3 сутки	Х3 = 4
□ на 4 сутки	Х4 = 0
□ на 5 сутки	Х5 = 0

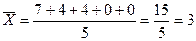
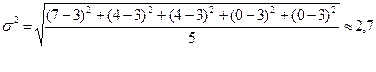
Далее подставляем следующие значения в формулу (4): коэффициент доверия t = 2 при вероятности Р = 0,954, дисперсия s² = 2,5 предельную ошибки выборки задаем в размере ∆ = 0,3 (или 30%); число единиц в генеральной совокупности N = 5000 человек. Отсюда численность выборки (n) составила:

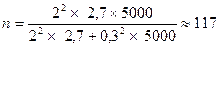
Эту величину мы округляем до 120 человек, т.е. установлена 2,5%-ная выборка.

Вопросы для самоконтроля

1. Охарактеризуйте выборку и ее составные элементы.

2. Что понимается в маркетинговых исследованиях под «репрезентативностью выборки»?

3. Опишите процесс планирования выборки.

4. Раскройте классификацию способов построения выборки.

5. Охарактеризуйте методы выборки, их преимущества и недостатки.

6. Какие методы расчета объема выборки Вы знаете, опишите их.

Список рекомендуемой литературы к теме 5:

1. Голубков Е.П. Маркетинговые исследования: теория, методология и практика. – М.: Издательство «Финпресс», 2008. – 416 с.

2. Малхотра, Нэреш К. Маркетинговые исследования. Практическое руководство, 3-е изд./ Пер. с англ. – М.: Издательский дом «Вильямс», 2008. – 960 с.: ил. – Парал. тит. англ.

3. Черчилль Г.А. Маркетинговые исследования. – СПб.: Питер, 2008. – 752 с.: ил. (Серия «Маркетинг для профессионалов»).

4. Маркетинговые исследования / Божук С.Г., Ковалик Л.Н. – СПб.: Питер, 2008. – 304 с.: ил. (Серия «Маркетинг для профессионалов»).

5. Ноэль Э. Массовые опросы: введение в практику демоскопии / Пер. с нем.- М: АВА-ЭСТРА, 2003.

6 Статистика рынка товаров и услуг: Учебник / И.К. Беляевский, Г.Д. Кулагина, А.В. Коротков и др., Под ред. И.К. Беляевского. – М.: Финансы и статистика, 2005. – 432 с.: ил.

7. Дюсембекова Ж.М. Маркетинговые исследования: Учебное пособие. – Алматы: Экономика, 2005. – 320 с.