Выборочный метод, виды выборки. Генеральная и выборочная совокупности
Равномерный закон распределения
Закон распределения непрерывной случайной величины называется равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение ( f(x) = const при a ≤ x ≤ b, f(x) = 0 при x < a, x > b.
Нормальный закон распределения.
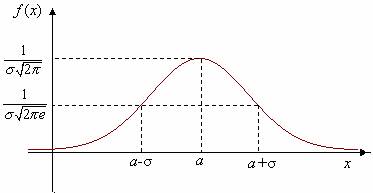
Непрерывная случайная величина X имеет нормальный закон распределения с параметрами а и , если её плотность вероятности f(x) имеет вид:
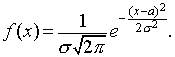
Показательный закон распределения
Показательным законом надежности называют функцию надежности, определяемую равенством
R(t) = 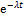 ,
,
где λ – интенсивность отказов.
Распределение Хи-квадрат. Распределение - Фишера-Снедекора
Пусть имеется несколько нормированных нормально распределенных случайных величин: Х1, Х2,…, Хп (ai = 0, σi = 1). Тогда сумма их квадратов
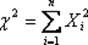
является случайной величиной, распределенной по так называемому закону «хи-квадрат» с k = nстепенями свободы; если же слагаемые связаны каким-либо соотношением, то число степеней свободы k = n – 1.
Плотность этого распределения
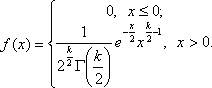
Здесь 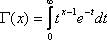 - гамма-функция; в частности, Г(n + 1) = n! .
- гамма-функция; в частности, Г(n + 1) = n! .
Следовательно, распределение «хи-квадрат» определяется одним параметром – числом степе-ней свободы k
Рассмотрим две независимые случайные величины Uи V, распределенные по закону «хи-квадрат» со степенями свободы k1 и k2 и образуем из них новую величину
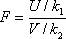
Ее распределение называют распределением F Фишера – Снедекора со степенями свободы k1 и k2. Плотность его распределения имеет вид
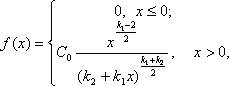
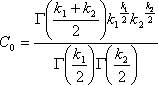
Таким образом, распределение Фишера определяется двумя параметрами – числами степеней свободы
Выборочный метод, виды выборки. Генеральная и выборочная совокупности
Выборочный метод применяется в тех случаях, когда проведение сплошного наблюдения невозможно или экономически нецелесообразно.
Часть единиц, отобранных для наблюдения, принято называть выборочной совокупностью, а всю совокупность единиц, из которых производится отбор, — генеральной.
Типы выборок
Выборки делятся на два типа:
- вероятностные
- невероятностные
1. Вероятностные выборки
1.1 Случайная выборка (простой случайный отбор)
Такая выборка предполагает однородность генеральной совокупности, одинаковую вероятность доступности всех элементов, наличие полного списка всех элементов. При отборе элементов, как правило, используется таблица случайных чисел.
1.2 Механическая (систематическая) выборка
Разновидность случайной выборки, упорядоченная по какому-либо признаку (алфавитный порядок, номер телефона, дата рождения и т.д.). Первый элемент отбирается случайно, затем, с шагом ‘n’ отбирается каждый ‘k’-ый элемент. Размер генеральной совокупности, при этом – N=n*k
1.3 Стратифицированная (районированная)
Применяется в случае неоднородности генеральной совокупности. Генеральная совокупность разбивается на группы (страты). В каждой страте отбор осуществляется случайным или механическим образом.
1.4 Серийная (гнездовая или кластерная) выборка
При серийной выборке единицами отбора выступают не сами объекты, а группы (кластеры или гнёзда). Группы отбираются случайным образом. Объекты внутри групп обследуются сплошняком.
2. Невероятностные выборки
Отбор в такой выборке осуществляется не по принципам случайности, а по субъективным критериям – доступности, типичности, равного представительства и т.д..
2.1. Квотная выборка
Изначально выделяется некоторое количество групп объектов (например, мужчины в возрасте 20-30 лет, 31-45 лет и 46-60 лет; лица с доходом до 30 тысяч рублей, с доходом от 30 до 60 тысяч рублей и с доходом свыше 60 тысяч рублей) Для каждой группы задается количество объектов, которые должны быть обследованы. Количество объектов, которые должны попасть в каждую из групп, задается, чаще всего, либо пропорционально заранее известной доле группы в генеральной совокупности, либо одинаковым для каждой группы. Внутри групп объекты отбираются произвольно. Квотные выборки используются в маркетинговых исследованиях достаточно часто.
2.2. Метод снежного кома
Выборка строится следующим образом. У каждого респондента, начиная с первого, просятся контакты его друзей, коллег, знакомых, которые подходили бы под условия отбора и могли бы принять участие в исследовании. Таким образом, за исключением первого шага, выборка формируется с участием самих объектов исследования. Метод часто применяется, когда необходимо найти и опросить труднодоступные группы респондентов (например, респондентов, имеющих высокий доход, респондентов, принадлежащих к одной профессиональной группе, респондентов, имеющих какие-либо схожие хобби/увлечения и т.д.)
2.3 Стихийная выборка
Опрашиваются наиболее доступные респонденты. Типичные примеры стихийных выборок – опросы в газетах/журналах, анкеты, отданные респондентам на самозаполнение, большинство интернет-опросов. Размер и состав стихийных выборок заранее не известен, и определяется только одним параметром – активностью респондентов.
2.4 Выборка типичных случаев
Отбираются единицы генеральной совокупности, обладающие средним (типичным) значением признака. При этом возникает проблема выбора признака и определения его типичного значения.
Полигон и гистограмма
Полигоном частот называют ломаную линию, отрезки которой соединяют точки 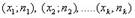 . Для построения полигона частот на оси абсцисс откладывают варианты, а на оси ординат – соответствующие им частоты и соединяют точки отрезками прямых.
. Для построения полигона частот на оси абсцисс откладывают варианты, а на оси ординат – соответствующие им частоты и соединяют точки отрезками прямых.
Полигон относительных частот строится аналогично, за исключением того, что на оси ординат откладываются относительные частоты.
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которой служат частичные интервалы длиною h, а высоты равны отношению 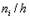 . Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии (высоте)
. Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии (высоте)