Анализ и интерпретация данных

Процесс анализа и интерпретации данных состоит в тщательно подготовленной работе по выявлению нежелательных погрешностей поиска интересующей информации. Предварительными аналитическими этапами являются:

1. Редактирование – установление некоторых стандартов минимального качества собранных данных. Этот процесс включает в себя просмотр и, если необходимо, исправление каждой анкеты или формы регистрации наблюдений.

Просмотр и внесение изменений зачастую выполняются в 2 стадии:

1.1 Полевое редактирование – предварительное редактирование, проводимое руководителем полевых исследований, которое строится таким образом, чтобы обнаружить наиболее бросающиеся в глаза пропуски и неточности средства сбора полных данных. Оно также необходимо для контроля поведения интервьюеров и внесения ясности в любого рода недопонимания ими направления деятельности, методов, специфических вопросов и т.п.

1.2 . Централизованное офисное редактирование – точная всеобъемлющая проверка и коррекция заполненных форм сбора данных, включая принятие решения о том, что с этими данными делать.

2. Кодирование – технический прием, с помощью которого данные распределяются по категориям; он связан со спецификацией альтернативных категорий или классов, в которые должны помещаться ответы, а самим классам должны назначаться кодовые номера.

3. Классификация/табулирование – упорядоченное сведение данных в таблицы или другой формат после подсчета частоты ответов на все вопросы. На данном этапе данные могут быть классифицированы по нескольким переменным.

Виды:

3.1. Простая табуляция – подсчет количества событий, которые попадаются в каждую категорию, когда категории базируются на одной переменной.

3.2. Перекрестная табуляция - подсчет количества событий, которые попадают в каждую из нескольких категорий, когда категория базируется на двух или более переменных, рассматриваемых одновременно.

Обычно закодированные исходные данные представляются в виде матрицы, столбцы которой содержат ответы на различные вопросы анкеты, а ряды - респондентов или изучаемые ситуации. Все это называется преобразованием исходных данных.

Далее проводится статистический анализ, т.е. определяются средние величины, частоты, корреляционные и регрессионные соотношения, осуществляется анализ трендов.

Выделяют пять основных видов статистического анализа, используемых при проведении маркетинговых исследований:

1. дескриптивный анализ;

2. выводной анализ;

3. анализ различий;

4. анализ связей;

5. предсказательный анализ.

Иногда эти виды анализа используются по отдельности, иногда - одновременно.

1. В основе дескриптивного анализалежит использование двух групп статистических мер.

Первая включает меры "центральной тенденции", или меры, которые описывают типичного респондента или типичный ответ (средняя величина, мода, медиана).

Вторая включает меры вариации, или меры, описывающие степень схожести или несхожести респондентов или ответов относительно "типичных" респондентов или ответов (распределение частот, размах вариации и среднее квадратическое отклонение).

Существуют и другие описательные меры, например меры асимметрии (насколько найденные кривые распределения отличаются от нормальных кривых распределения). Однако они используются не столь часто, как вышеупомянутые, и не представляют особого интереса для заказчика.

Анализ, в основе которого лежит использование статистических процедур (например, проверка гипотез) с целью обобщения полученных результатов на всю совокупность, называется выводным анализом. Вывод является видом логического анализа, направленного на получение общих заключений о всей совокупности на основе наблюдений за малой группой единиц данной совокупности.

Выводы делаются на основе анализа малого числа фактов. Например, если два ваших товарища, имеющие одну и ту же марку автомобиля, жалуются на его качество, то вы можете сделать вывод о низком качестве данной марки автомобиля в целом.

Статистический же вывод основан на статистическом анализе результатов выборочных исследований и направлен на оценку параметров совокупности в целом. В данном случае результаты выборочных исследований являются только отправной точкой для получения общих выводов.

Анализ различийиспользуется для сравнения результатов исследования двух групп (двух рыночных сегментов) с целью определения степени реального различия в их поведении, в реакции на одну и ту же рекламу и т.п.

Проверка существенности различий заключается в сопоставлении ответов на один и тот же вопрос, полученных для двух или более независимых групп респондентов. Кроме того, в ряде случаев представляет интерес сравнение ответов на два или более независимых вопросов для одной и той же выборки.

Анализ связейнаправлен на определение систематических связей (их направленности и силы) переменных. Например, его предметом может быть определение, как увеличение затрат на рекламу влияет на рост сбыта.

Очень часто специалист по маркетингу ищет ответы на вопросы типа: "Увеличится ли показатель рыночной доли при увеличении числа дилеров?", "Есть ли связь между объемом сбыта и рекламой?" Такие связи не всегда имеют причинно-следственный характер, а могут иметь просто статистическую природу. В приведенных выше вопросах можно определенно говорить о влиянии одного фактора на другой. Однако степень влияния изучаемых факторов может быть различной; скорее всего, влияние при этом могут оказывать также какие-то другие факторы.

Предсказательный анализиспользуется в целях прогнозирования развития событий в будущем - например, путем анализа временных рядов. Специалист по маркетингу хорошо знает, насколько важна хорошая упаковка для продаваемого товара. Результаты маркетинговых исследований также являются товаром и поэтому должны быть хорошо "упакованы".

Средние величины

Средняя величина (среднее, среднее значение) дает представление о наиболее "типичном" или "центральном" значении (центральной тенденции) в интервале изменения переменной (переменной величины). Например, средняя цена, средний объем продаж - подобные термины часто используются в практической работе специалиста по маркетингу. В качестве средней величины чаще всего рассматриваются мода, медиана, средняя арифметическая и средняя геометрическая.

Мода - наиболее часто встречаемая величина в наборе данных. Это наиболее "типичное" значение среди данных. Оно может быть определено непосредственно из данных таблицы или графика. В графическом изображении данная величина соответствует величине на оси абсцисс, при которой соответствующая величина у является наибольшей. Недостаток наиболее часто встречаемой величины состоит в том, что она учитывает только соотношения величин, изменения же величин за пределами моды остаются неучтенными.

Пример расчета моды:

Упаковочная машина упаковывает по 100 канцелярских скрепок в маленькие пластмассовые футляры. Проверка 25 пластмассовых футляров дала следующий результат:

Наиболее часто встречаемой здесь величиной со значением признака 7 является количество в 100 штук.

Медиана (центральная величина) - это среднее, полученное путем выявления "центрального" значения в перечне данных, расположенных в ранжированном порядке. Медиана не учитывает экстремальных значений. Если налицо нечетное количество величин, например N = 9, то центральная величина рассчитывается следующим образом:

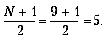
В предыдущем примере наиболее часто встречаемая величина определялась среди следующих величин: 92, 95, 97, 98, 99, 100, 101, 102, 107. Медианой является здесь 99 (5-я величина).

Средняя арифметическая учитывает каждое значение признака, в том числе экстремальные и случайные величины. Каждое изменение значений признака влияет на среднюю величину. Выделяют невзвешенную среднюю арифметическую и взвешенную среднюю арифметическую.

Невзвешенная средняя арифметическая получается путем деления суммы всех значений на их количество:

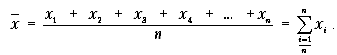
Средняя арифметическая чисел 2, 3, 5, 7 и 8 следующая:

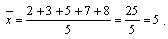
Во взвешенной средней арифметической у отдельных значений учитывается определенный признак, например количество или вес:

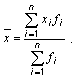
Предположим, что отдельным значениям признака xi (х1, х2, х3 ... хn) соответствует разный вес или разная частотность fi:

Если сумму умноженных на соответствующий вес значений признака 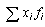=36 разделить на сумму частотностей 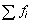=12 , то в результате получится взвешенная средняя арифметическая, равная 3.

Пример расчета средних арифметических:

За 1 кг нескольких товаров были рассчитаны соответственно следующие цены: товар А - 12 руб., товар Б - 40 руб., товар В - 60 руб. и товар Г - 70 руб.

Проданное количество товаров составило:

товар А - 500 кг товар В - 600 кг

товар Б - 2500 кг товар Г - 1400 кг

а) невзвешенная средняя арифметическая равна:

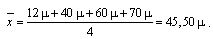
б) расчет взвешенной средней арифметической

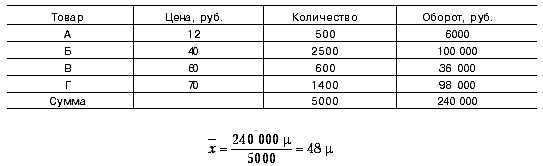
Средняя геометрическая также учитывает все значения признака в наборе данных. Знак корня способствует, правда, тому, что в средней геометрической менее сильно, чем в средней арифметической, сказывается влияние экстремальных значений. Средняя геометрическая применяется в большинстве случаев для расчета средних темпов роста:

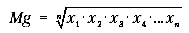
Например, объем продаж предприятия за последние четыре года изменялся следующим образом:

1-й год - увеличение 7%: 1 + 0,07 = 1,07;

2-й год - увеличение 9%: 1 + 0,09 = 1,09;

3-й год - уменьшение 3%: 1 - 0,03 = 0,97;

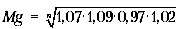
Mg = 1,0364

Средний темп роста составляет 0,0364 (если предварительно вычесть 1). Обороты предприятия за последние четыре года увеличились, таким образом, в среднем на 3,64%.

Показатели вариации

Совокупность изучаемых данных (статистической массы) может иметь разную структуру. Например, две совокупности могут иметь совпадающие средние значения, и, несмотря на это, у них может быть разная структура:

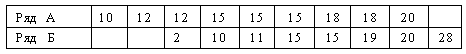
Средняя арифметическая и медиана составляют в обоих рядах соответственно 15, и, несмотря на это, у них разная структура. Значения признака ряда Б отчетливо больше рассеяны, чем ряда А.

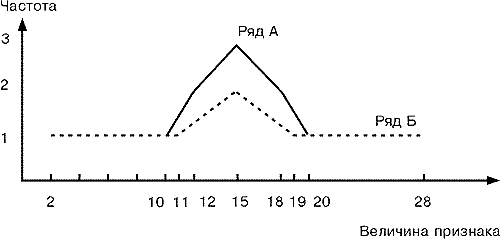
Вариацией значений какого-либо признака в совокупности называется различие его значений у разных единиц данной совокупности в один и тот же период или момент времени. В маркетинге понятие вариации часто характеризует величину несхожести (схожести) ответов респондентов на определенный вопрос. Результаты ответов на вопросы опроса обычно представляются в форме кривой распределения. При высокой схожести ответов говорят о малой вариации (узкая кривая распределения), а при низкой схожести ответов - о высокой вариации (широкая кривая распределения).

Обычно используют следующие меры вариации (рассеивания): размах вариации, среднее отклонение, среднее квадратическое отклонение, дисперсию и коэффициент вариации.

Размахом вариации является разница между наибольшим и наименьшим значениями признака.

Размах вариации в ряду А: 20-10=10 и в ряду Б: 28-2=26.

Размах вариации легко рассчитывается. Однако он имеет недостаток, который состоит в том, что учитываются только оба экстремальных значения.

Среднее отклонение учитывает отдельное отклонение каждого значения признака статистической массы от среднего значения этой массы.

Простое среднее отклонение d статистической массы из n элементов со значениями признака от x1 до хn рассчитывается по следующей формуле:

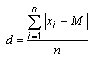
Разница | хi - М | представляет собой абсолютную разницу между значением признака хi и средним значением М 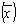. Сумма отдельных отклонений всех значений признака от среднего арифметического делится на число значений признака.

Пример расчета простого среднего отклонения.

Среднее отклонение ряда Б от среднего значения 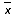= 15 может быть рассчитано следующим образом:

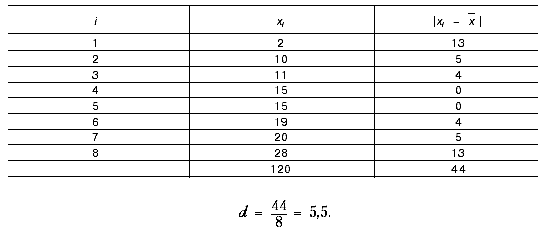
В среднем значения отклоняются от среднего арифметического или от центральной величины на 5,5.

Взвешенное среднее отклонение учитывает тот факт, что разные значения признака возникают с разными частотами:

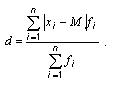
Отдельное отклонение каждого значения признака от среднего значения умножается на соответствующую частоту. Сумма всех этих результатов делится на сумму частот.

Пример расчета взвешенного среднего отклонения ряда А от среднего значения 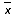= 15:

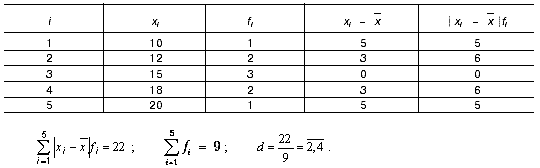
Среднее квадратическое отклонение (стандартное отклонение), обычно обозначаемое  или s, соотносит отклонения отдельных величин признака только со средним арифметическим. Расчет здесь похож на расчет среднего отклонения. Отдельные отклонения от среднего арифметического возводятся в квадрат, и затем извлекается квадратный корень:

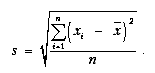
Простое среднее квадратическое отклонение рассчитывается по формуле

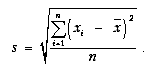
Взвешенное среднее квадратическое отклонение рассчитывается по формуле

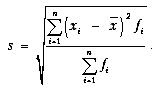
Например, взвешенное среднее квадратическое отклонение s ряда А от среднего арифметического 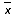=15 рассчитывается следующим образом:

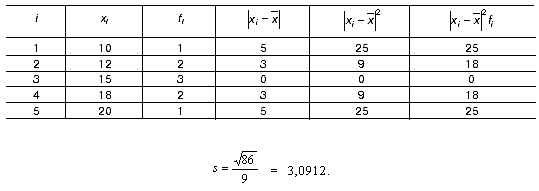
Дисперсияs² получается путем возведения в квадрат среднего квадратического отклонения. В предыдущем примере дисперсия

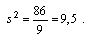
Среднее квадратическое отклонение имеет такую же размерность, как и признаки статистической массы, например рубли, килограммы, поэтому их нельзя объединять напрямую. Такое объединение можно делать в случае использования дисперсии. В то время как дисперсия используется преимущественно в теоретической статистике, стандартное отклонение s имеет большее значение для практических расчетов.

При нормальном распределении по Гауссу, на основе теории выборок, элементы ряда следующим образом располагаются вокруг среднего арифметического:

68,3% в границах от х + 1 ;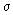

95,5% в границах от х + 2 ;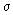

99,7% в границах от х + 3 .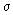

Коэффициент вариации V является частным от среднего квадратического отклонения и средней арифметической:

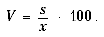
В отличие от других мер вариации коэффициент вариации не является "овеществленной" мерой разброса. Размерность значений признака статистической массы теряется, но распределения с различными единицами сопоставимы.