Преодоление препятствий на пути к решению задач

Мы должны еще раз подчеркнуть, что мыслительная установка как таковая — вещь полезная, она позволяет решающему задачу сосредото­читься на конструктивных направлениях и избежать бессмысленных дей­ствий. Однако те же самые установки могут создать затруднения, застав­ляя нас задаться вопросом о том, как можно их преодолеть. Мы уже от­мечали важное значение знакомых программ и алгоритмов. Но что нам делать, если не удается выделить подзадачи или нам незнаком тот алго­ритм, который требуется для решения?

Обратное действие

Одним из полезных приемов при решении задач является обратное действие, когда поиск решения начинается с конца и идет в обратном направлении, двигаясь к исходной точке. Рассмотрим такую задачу.

Количество водяных лилий на поверхности озера удваивается каждый день. В первый день лета на озере росла только одна лилия. Потребовалось 60 дней, чтобы озеро полностью покрылось лилиями. В какой по счету день озеро было покрыто наполовину?

Задача может быть решена следующим образом. В первый день есть одна лилия; во второй — две лилии; в третий — четыре и т.д. При дос­таточном терпении этот метод приведет нас к заключению, что на 60-й день на озере было 580 млрд. лилий; половина из них — это 290 млрд., которые появились бы на 59-й день. Однако существует очень простой путь, который избавляет от этих громоздких вычислений: если озеро покрыто полностью на 60-й день, оно должно быть покрыто наполовину в предыдущий день, поскольку количество лилий удваивается каждый день; следовательно, правильный ответ — 59-й день <...>.

Решение по аналогии

В качестве еще одного приема, помогающего при решении трудных задач, можно предложить решение по аналогии, поскольку многие зада­чи похожи друг на друга. Школьный психолог часто сталкивается с тем, что проблема, о которой ему рассказывают сегодня, напоминает ту, кото­рая была несколько месяцев назад, и первый опыт может помочь ему справиться со второй. Ученый, пытающийся дать объяснение новому явле­нию, часто находит ответ, анализируя прошлые явления, схожие с дан­ным. Аналогии сыграли важнейшую роль в истории науки; вспомним ученых, которые расширяли свои знания о газах, сравнивая молекулы с бильярдными шарами, или давали объяснение работе сердца, сравнивая его с насосом.

В одном из исследований участникам была предложена такая за­дача.

У больного — неоперабельная опухоль в брюшной полости. Существуют та­кие лучи, которые при достаточной интенсивности могут разрушить эту опу­холь. Однако при такой интенсивности лучи разрушат и здоровую ткань вок­руг опухоли (стенки желудка, брюшные мышцы и т.д.). Как избавить боль­ного от опухоли, не причиняя вреда здоровой ткани, через которую должны пройти эти лучи?²

Эта задача чрезвычайно сложна: в первой группе 90% участников не смогли ее решить. Вторая группа справилась намного лучше. До того как решать задачу с опухолью, они прочитали историю о генерале, ко­торый хотел захватить крепость. Для этого ему требовалась большая ар­мия солдат, но все дороги к крепости были заминированы. Маленькая группа солдат могла пройти по дороге, но более крупная группа обяза­тельно подорвалась бы на мине. Как же генералу провести к крепости всех солдат? Он разделил свою армию на маленькие группы и перепра­вил их по разным дорогам. По данному им сигналу все группы напра­вились к крепости, где объединились. После успешной атаки они захва­тили крепость.

По своей структуре история о крепости похожа на задачу с опухо­лью. В обоих случаях решение заключается в разделении «боевой силы» таким образом, чтобы она подходила из нескольких разных источников. Для того, чтобы уничтожить опухоль, сквозь здоровую ткань нужно пропустить несколько слабых лучей, каждый — разным путем. Лучи скон­центрируются на опухоли и окажут суммарное воздействие (рис. 5).

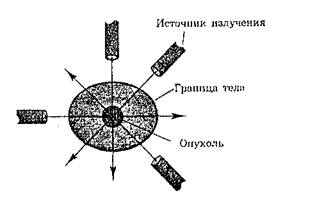
Рис. 5. Решение задачи с облучением опухоли

Несколько слабых лучей исходят из различных точек снаружи та­ким образом, чтобы соединиться на месте опухоли. В этом месте доза облучения будет сильной, так как в данной точке суммируется их общее действие. Но поскольку каждый луч сам по себе слаб, лучи не причиня­ют вреда здоровой ткани, окружающей опухоль¹

Без подсказок, инструкций или знания аналогичных случаев 90% участников первой группы не смогли решить задачу с опухолью. Одна­ко, когда им дали прочитать историю о крепости и сказали, что она им поможет, большинство (80%) решило задачу. Безусловно, аналогии чрез­вычайно полезны. Но недостаточно просто знать историю о крепости, испытуемые должны были понять и то, что эта история связана с дан­ной задачей. Удивительно, но многие не увидели здесь никакой анало­гии: участникам еще одной группы дали прочитать историю о крепости, но не намекнули на то, что эта история относится к их задаче. При та­ких условиях только 30% испытуемых решило задачу с опухолью.

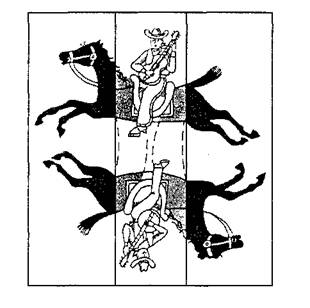
Рис. 6. Решение задачи про всадников и лошадей

Для того чтобы решить эту задачу, необходимо изменить перцеп­тивную установку. Часть А нужно повернуть на 90°, чтобы лошади ока­зались в вертикальной позиции. Теперь можно заметить, что голову од­ной (вертикальной) лошади можно совместить с задней частью другой. Последний шаг состоит в том, чтобы наложить Б на середину А.

А.Н. Леонтьев