Расчёт наклонных сечений балки на прочность по поперечной силе и изгибающему моменту
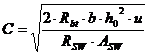 (51)
(51)
Rbt = 1,5 МПа – расчётное сопротивление бетона растяжению.
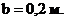
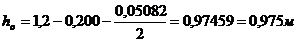
u = 0,1 м – шаг хомутов, 2Æ8мм.
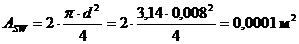 – площадь хомутов (52)
– площадь хомутов (52)
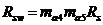 , где
, где 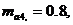
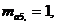 – коэффициенты условий работы арматуры (53)
– коэффициенты условий работы арматуры (53)
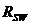 = 0,8*1*265 = 212 МПа
= 0,8*1*265 = 212 МПа
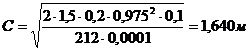
С≤2ho, 1,640 м ≤ 1,950 м.
Проверка шага хомутов:
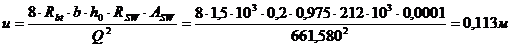 (54)
(54)
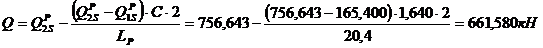 (55)
(55)
Пересчитываем значение С с учетом шага хомутов:
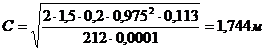
Условие обеспечения прочности по сжатому бетону между наклонными трещинами имеет вид:
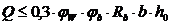 (56)
(56)
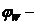 коэффициент условия работы хомутов с бетоном.
коэффициент условия работы хомутов с бетоном.
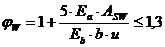 (57)
(57)
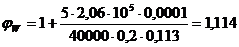
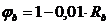 (58)
(58)
φb = 1 - 0,01*30 = 0,7
Q ≤ 0,3*1,114*0,7*30*10³*0,2*0,975 = 1368,549 кН
661,580 кН < 1368,549 кН (условие выполнено)
Условие прочности бетона при поперечной нагрузке:
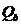 <
< 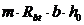 (59)
(59)
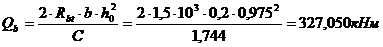 (60)
(60)
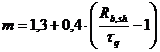 (61)
(61)
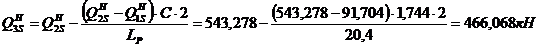 (62)
(62)
Коэффициент приведения арматуры к бетону
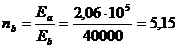 (63)
(63)
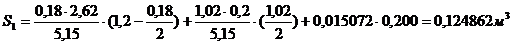
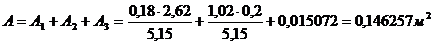
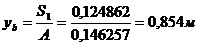
Статический момент нижней части:
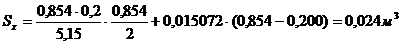
Момент инерции:
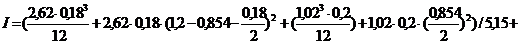
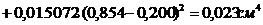
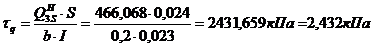
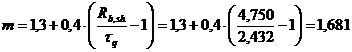
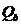 <
< 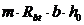
327,050 < 1,681*1,50*10³*0,2*0,975
327,050 кН < 491,693 кН (условие выполнено)
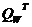 –усилие, воспринимаемое горизонтальной арматуройкН,
–усилие, воспринимаемое горизонтальной арматуройкН,
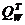 = 1000
= 1000 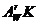 , где
, где 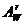 – площадь горизонтальной арматуры (64)
– площадь горизонтальной арматуры (64)
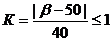 (65)
(65)
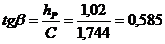 (66)
(66)
β = 30˚
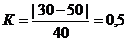
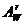 =
= 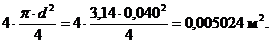 (4 стержня Æ 40 мм)
(4 стержня Æ 40 мм)
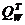 = 1000*0,005024*0,5= 2,512 кН
= 1000*0,005024*0,5= 2,512 кН
Условие обеспечения прочности по арматуре:
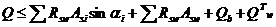 (67)
(67)
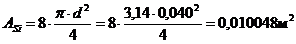 (8 стержней Æ 40 мм)
(8 стержней Æ 40 мм)
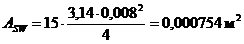
661,580 ≤ 265*10³*0,010048*sin45+0,000754*212*10³ + 327,050 + 2,512
661,580 кН ≤ 2371,953 кН (условие выполняется)
Расчет наклонных сечений по изгибающему моменту следует выполнять из условия:
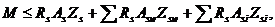 (68)
(68)
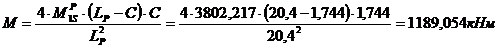 (69)
(69)
1189,054≤265*10³*0,005024*1,020+212*0,000754*(10+123+236+349+462++575+688+801+914+1027+1140+1253+1366+1479+1592)+265*103*0,010048* *(0,436+1,263)
1189,054 кН ≤ 7802,522 кН (условие выполняется)
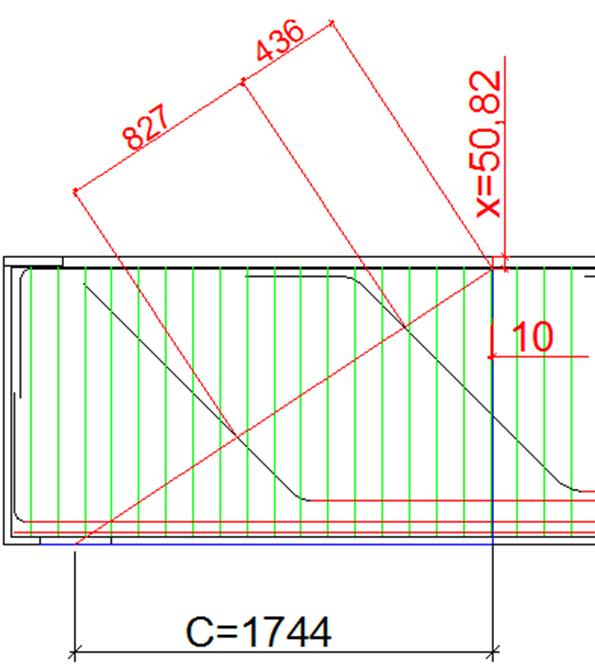
Рис.9. Расчет наклонных сечений
Расчет и конструкция плиты балки
На изображении схемы установки колеса вдоль и поперек пролета балки, схема армирования плиты и схема распределения давления от колеса. Отпечатки колеса а1 и b1 на покрытии ездового полотна принимаются, соответственно для Н14 0,2м и 0,8м, для А14 – 0,2м и 0,6м. Усилие Р давления на колесо для Н14 – 126 кН, для А14 – 70 кН.
Н14:
Размеры площадки а2 и b2 передачи усилий от колеса на поверхность плиты:
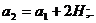 (70)
(70)
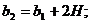 (71)
(71)
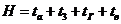 (72)
(72)
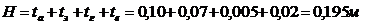
а2 = 0,2 + 2*0,195 = 0,59м
b2 = 0,8 + 2*0,195 = 1,19м
При этом расчетная ширина плиты, воспринимающая изгибающий момент от давления колеса
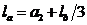 , но не менее 2/3 lb. (73)
, но не менее 2/3 lb. (73)
la = 0,59 + 1,50/3 = 1,090≥ 1,000
Изгибающие моменты в сечениях:
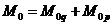 (74)
(74)
Балочный изгибающий момент от постоянных нагрузок:
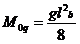 (75)
(75)
где g – расчетная нагрузка собственного веса конструкций:
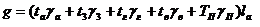 (76)
(76)
g=(0,10·22,56+0,07·24,53+0,005·14,72+0,02·23,54+0,10·24,53)·1,090 = =7,598 кН/м
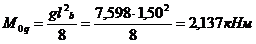
Балочный изгибающий момент от временной нагрузки определяется в виде:
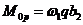 , (77)
, (77)
где 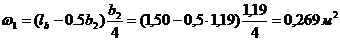 – площадь участка линии влияния М0 в границах распределения временной местной нагрузки.
– площадь участка линии влияния М0 в границах распределения временной местной нагрузки.
Усилия от временных нагрузок определяются от Н14 и А14:
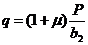 – интенсивность распределения Н14 при Р=126 кН и
– интенсивность распределения Н14 при Р=126 кН и 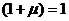 для Н14, (78)
для Н14, (78)
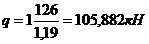
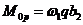 = 0,269*105,882*1,19 = 33,894 кНм
= 0,269*105,882*1,19 = 33,894 кНм
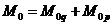 =2,137+33,894 = 36,031 кНм.
=2,137+33,894 = 36,031 кНм.
А14:
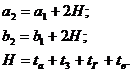
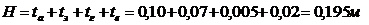
а2 = 0,2 + 2*0,195 = 0,59 м
b2 = 0,6 + 2*0,195 = 0,99 м
Усилия от временных нагрузок определяются от А14:
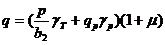 – интенсивность распределения А14 при
– интенсивность распределения А14 при
Р=70 кН (79)
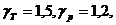
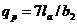 = 7*1,090/0,99 = 7,707 кН/м (80)
= 7*1,090/0,99 = 7,707 кН/м (80)
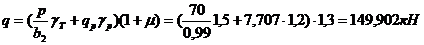
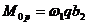 =0,249*149,902*0,99=36,952 кНм
=0,249*149,902*0,99=36,952 кНм
где 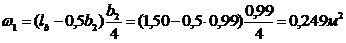
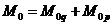 =1,671+ 36,952= 38,623 кНм
=1,671+ 36,952= 38,623 кНм
Изгибающие моменты в сечениях 1-1 и 2-2 (М1 и М2) определяются через балочный момент М0, который определяется для разрезной балки пролетом lb. Балочный момент определяется от совместного действия временных и постоянных нагрузок (в качестве временной нагрузки следует рассмотреть А14 и Н14 и выбрать из них ту нагрузку, которая вызывает наибольший изгибающий момент):
Выбираем М0 от А14, М0=38,623 кНм
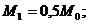 (81)
(81)
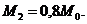 (82)
(82)
M1 = 0,5*38,623 = 19,312 кН·м
M2 = 0,8*38,623 = 30,898 кН·м
В качестве расчётного:
Mоп = 30,898 кН·м
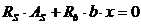
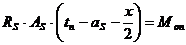
пусть высота сжатой зоны: 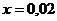 м,
м, 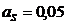 м
м
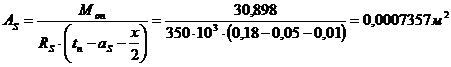
возьмём диаметр d = 12 мм
d = 12 мм 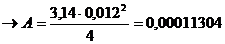 м2.
м2.
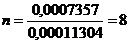 стержней
стержней
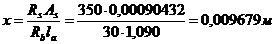
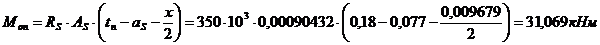
М2 ≤ Мпред ≤ 1,05М2
30,898 кНм ≤ 31,069 кНм ≤ 32,4430, кНм (условие выполнено)
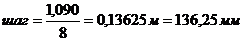 (83)
(83)
Примем шаг кратный 25, т.е. 125 мм, для удобного изображения расположения арматуры
Окончательно принимаем:8 Æ12 АIII с шагом 136,25 мм.
