Прямое измерение ощущений. Методы прямого измерения. Закон Стивенса

С. Стивене

ПСИХОФИЗИКА СЕНСОРНОЙ ФУНКЦИИ *

Исследование природы сенсорного процесса на­чинается с психофизики — дисциплины, зародившей­ся сто лет назад и изучающей ответные реакции орга­низма на воздействие энергий окружающей среды. <...>

С самого начала необходимо признать, что пси­хофизике зачастую не удавалось выполнить стоящую перед ней задачу на должном уровне. Ее задача не из легких. Прежде всего всякий раз, когда выдвигались предположения о возможности подвергнуть ощуще­ние упорядоченному количественному исследова­нию, старые предрассудки, унаследованные в основ­ном от дуалистической метафизики, порождали це­лый ряд упорных возражений. Вы не можете, гово­рили критики, измерить внутреннюю, индивидуаль­ную, субъективную силу того или иного ощущения. Может быть, это и так, говорим мы, в том смысле, в каком это понимают те, кто нам возражает. Одна­ко в другом и весьма полезном смысле сила ощуще­ния может быть, как мы увидим далее, с успехом определена количественно. Нам нужно оставить в стороне споры о внутренней жизни разума. Мы дол­жны задать себе разумные объективные вопросы об отношениях между входом и выходом сенсорных преобразователей, учитывая при этом то, как эти отношения раскрываются в поведении организмов, будь то животные или люди.

Другая трудность состоит в том, что у психофи­зики было несчастливое детство. Хотя еще в пятиде­сятых годах XIX века Плато сделал нерешительную попытку правильно определить форму функции пу­тем соотнесения воспринимаемой интенсивности с интенсивностью раздражителя, тем не менее его го­лос был заглушён Фехнером, который сковал раз­витие только что зародившейся дисциплины, обре­менив ее глубоко ошибочным "законом", носящим его имя (Стивене, 1957). Быть может, самой трудной задачей, стоящей перед нами, является освобожде­ние науки от господства столетней догмы, утверж­дающей, что интенсивность ощущения возрастает как логарифм интенсивности раздражителя (закон Фех-нера). На самом деле данное отношение вовсе не выражается логарифмической функцией. К настоя­щему времени на примере более чем двадцати сен­сорных континуумов ** показано, что кажущаяся или субъективная величина возрастает как степенная функция от интенсивности раздражителя и что пока­затели степенной функции лежат в пределах от 0,33 для яркости до 3,5 для электрического раздражения

(60 Гц) пальцев руки. Иными словами, по-видимо­му, существует простой и повсеместно действующий психофизический закон, — закон, о котором одно время догадывался Плато и от которого он впослед­ствии отказался. Этот закон целиком соответствует не только все увеличивающемуся потоку эмпиричес­ких данных, но также и известным разумным прин­ципам построения теории(./7ьк>с, 1959). О степенном законе более подробно будет сказано далее, здесь же следует сказать несколько слов о Фехнере. <...>

Выводя свой логарифмический закон, Фехнер ошибочно предполагал, что минимальный прирост ощущения (AS) будто бы есть постоянная величина на всем протяжении психологической шкалы. Хотя он хотел предположить, что постоянным является отношение едва заметного изменения раздражителя (ДА²)² * к его исходной величине (R), т.е.

AR

----- = к (закон Вебера),

R

у него получилось, что постоянно AS. Из этих двух предположений он вывел отноше­ние

S=k log/?

и тем самым нанес большой вред всему делу.<...> Предположим, что Фехнер принял бы положе­ние о постоянстве отношения не только для е. з. р. стимуляции ДА, но также и для субъективного кор­релята е. з. р. — AS. Тогда он смог бы написать:

AS

AR

откуда следовало бы, что психическая величина 5 является степенной функцией физической вели­чины А. Однако он отбросил это предположение, когда оно впервые было сделано Брентано. В резуль­тате временной победы Фехнера в психофизике от­крылся период бесплодных исследований, когда ка­залось, что нет более интересной работы, чем изме­рение е.з.р. Так логарифмический закон стал "пещер­ным идолом" **.

Но довольно о прошлом. Начиная с 30-х годов XX века значение психофизики стало восстанавли­ваться. Новый интерес к очень старой проблеме сен­сорного ответа возник благодаря изобретению мето­дов, описывающих соотношение входа и выхода сен­сорных систем. Эти методы показывают, что сенсор­ные ответы возрастают по степенному закону. При изучении поведения так редко удается показать, что простое отношение сохраняется при самых различ­ных видах стимуляции, что широкое распростране­ние и постоянство степенного закона действитель­но приобретают большое значение.

* Хрестоматия по ощущению и восприятию / Под ред. Ю.Б.Гиппенрейтер, М.Б.Михалевской. М.: Изд-во Моск. ун-та, 1975. С. 261-269.

** Континуум - непрерывный ряд переменных величин, т. е. такой ряд величин, в котором всегда между двумя значениями, как бы близки они ни были, можно взять третье.<...>

* AR - минимальное изменение величины раздражителя, не­обходимое для возникновения ощущения едва заметного раз­личия, принято называть едва заметной разницей (е. з. р.), или различительной ступенью.

** Игра слов: den по-английски означает пещера, а также ка бинет ученого. (Примечание переводчика.)

Конечно, можно себе представить, что ощуще­ния всех модальностей возрастают одинаково с уве­личением интенсивности стимуляции. На самом деле это совсем не так, и это легко показать при помощи элементарного сравнения. Заметьте, что, например, происходит при удвоении освещенности пятна све­та и, с другой стороны, силы тока (частота 60 Гц), пропускаемого через палец. Удвоение освещенности пятна на темном фоне удивительно мало влияет на его видимую яркость. По оценке типичного наблю­дателя кажущееся увеличение составляет всего лишь 25%. При удвоении же силы тока ощущение удара увеличивается в десять раз. <...>

При более близком рассмотрении, однако, об­наруживается, что у яркости и удара имеется одна общая главнейшая черта. В обоих случаях психологи­ческая величина S относится к физической величи­не R следующим образом: S = kR'.

Показатель и принимает значение 0,33 для ярко­сти и 3,5 — для удара. Значение к зависит только от выбранных единиц. <...>

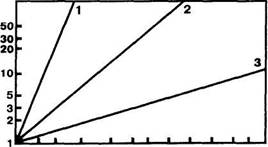
Степенная функция имеет то преимущество, что при использовании логарифмического масштаба на обеих осях она выражается прямой линией, наклон которой соответствует значению показателя. Это вид­но на рис. 1: медленное увеличение яркостного кон­траста и быстрое усиление ощущения удара электри­ческим током. Для сравнения на этом рисунке пока­зана также функция оценки видимой длины линий, сделанной несколькими наблюдателями. Здесь, как и следовало ожидать, показатель функции лишь не­много отличается от 1,0. Иначе говоря, для большин­ства людей отрезок 100 см кажется вдвое длиннее, чем отрезок 50 см. <...>

В настоящее время уже известно свыше 25 кон­тинуумов, на которые, как было показано, распро­страняется по крайней мере в первом приближении степенной закон. В своей практике автор еще ни разу не встретил исключения из этого закона (отсюда и смелость называть эту зависимость законом).

100

2 3

20 50 100 300 1000 30 200 500

Рис. 1. Зависимости субъективной величины (ощущения) от величины раздражителя для 3-х мо­дальностей, представленные в логарифмическом мас­штабе на обеих осях:

1 - электрический удар; 2 - кажущаяся длина; 3 - яркость; абсцисса - величина раздражения (ус­ловные единицы); ордината — психологическая ве­личина (произвольные единицы)

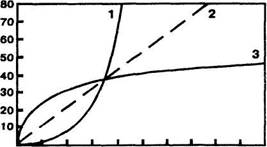
На рис. 2 — те же самые три функции представ­лены в линейных координатах.

О 10 20 30 40 50 60 70 80 вО 100

Рис. 2. Те же зависимости, что и на предыду­щем рисунке, представленные в линейных коорди­натах. Форма функции вогнутая или выпуклая, зави­сит от величины показателя степени: л больше или меньше 1,0. Обозначения кривых и осей те же, что и на предыдущем рисунке

В табл. 1 указаны показатели степенных функций некоторых из исследованных континуумов.

Межмодальные сравнения

Немного найдется ученых, которые бы не ощу­щали неудовлетворения вышеописанным методом, надежность которого всецело полагается на выраже­ние мнения наблюдателей и зависит от того, насколь­ко хорошо они знают числовую систему. Эта неудов­летворенность методом вполне обоснована, ибо поверхностные знания чисел, особенно отсутствие понятия о пропорции, естественно, затрудняет спо­собность некоторых наблюдателей хорошо выполнить свою роль в этих экспериментах. Обозначение силы ощущения числом не является чем-то таким, что человек выполняет с большей точностью и уверен­ностью, хотя обыкновенный выпускник высшего учебного заведения, как правило, может произво­дить целый ряд непротиворечивых числовых оценок.

Однако интересно не то, уверены или не увере­ны мы в полноценности этого метода. Интересно другое, можем ли мы подтвердить правильность сте­пенного закона, вообще не предлагая наблюдателям производить численные оценки? Если да, то можем ли мы проверить правильность отношений между по­казателями, приведенными в табл. 1? Утвердитель­ный ответ на этот вопрос дают результаты проведе­ния эксперимента по методу, согласно которому наблюдатель производит уравнивание интенсивнос-тей ощущений двух различных модальностей. Посред­ством таких межмодальных сравнений, производи­мых при разных интенсивностях стимуляций, мож­но получить "функцию равных ощущений", а затем сравнить ее с такой же функцией, предсказанной на основании величин показателей для этих двух мо­дальностей.

Если обе модальности при соответствующем выборе единиц описываются уравнениями:

Sr ^КГ ^{и S}2= V

и если субъективные величины 5, и S₂ уравнива­ются путем межмодального сравнения на различных уровнях стимуляции, то результирующая функция

Таблица 1

Характерные показатели степенных функций, со­относящие психологическую величину с величиной сти­муляции в протетических континуумах

Континуум	Показатель	Условия раздражения
Громкость	0,6	Бииауральное
Громкость	0,54	Моноуральное
Яркость	0,33	Размер раздражителя -5°,
		наблюдатель адаптирован к темноте
Яркость	0,5	Точечный источник света в
		условиях тем новой адаптации
Светлота	1,2	Отражательная способность серой
		бумаги
Запах	0,55	Кофе
Запах	0,6	Гептан
Вкус	0,8	Сахарин
Вкус	1,3	Сахароза
Вкус	1,3	Соль
Температура	1,0	Холод на руку
Температура	1,6	Тепло на руку
Вибрация	0,6	250 Гц на палец
Вибрация	0,95	60 Гц на палец
Длительность	1,1	Раздражитель - белый шум
Период повторения	1,0	Свет, звук, прикосновение,
		электрическое раздражение
Расстояние между	1,3	Толщина деревянных брусков
пальцами
Давление на ладонь	1,1	Статическое усилие на кожу
Тяжесть	1,45	Поднятие тяжести
Усилие сжатия	1,7	Точный ручной динамометр
кисти руки
Аутофонический	1,1	Звуковое давление при
уровень		произнесении звуков
Электрическое	3,5	Ток 60 Гц, пропущенный через
раздражение		пальцы

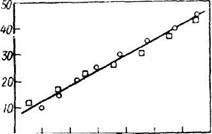
ратики - средние уровни звука в децибелах, к которым подравнива­лась вибрация. Оси координат даны в децибелах относительно ориенти­ровочно определенных порогов обо­их раздражителей.

Интересно, что на рис. 3 наклон линии равен 0,6, т. е. близок к на­клону, требуемому отношением по­казателей двух функций, получен­ных отдельно для звука и вибрации методом оценки величин. Эта зави­симость в основном линейна, и, следовательно, в диапазоне исполь­зованных стимулов как громкость, так и вибрация подчиняются сте­пенному закону.

равных ощущений примет вид: Д,^т = Л,"

Или в логарифмах log R, = — log Я,.

¹ т ²

Иначе говоря, в логарифмических координатах функция равных ощущений будет прямой линией, наклон которой определяется отношением двух дан­ных показателей.

Что касается самого эксперимента, то вопрос заключается в том, способны ли наблюдатели де­лать межмодальные сравнения и могут ли быть пред­сказаны эти сравнения, исходя из шкалы отноше­ний кажущихся величин, определяемой независимо путем оценки величин? Способность наблюдателей высказывать простые суждения о кажущемся равен­стве была твердо установлена в другом контексте. <...>

Звук и механическая вибрация являются такими стимулами, кажущуюся силу которых приравнять сравнительно легко. В качестве звука в эксперимен­тах использовался шум умеренно низкой частоты. Вибрация имела постоянную частоту (60 Гц) и по­давалась на кончик среднего пальца (Стивене, 1959).

Соотнесение кажущейся интенсивности звука и вибрации проводилось в двух дополняющих друг дру­га экспериментах. В одном из них звук подравнивался под вибрацию, в другом вибрация подравнивалась под звук. И звук и вибрация подавались одновременно. 10 наблюдателей производили в каждом эксперимен­те два подравнивания на каждой интенсивности.

Результаты этих экспериментов приведены на рис. 3. Кружочки обозначают средние уровни вибрации в децибелах, к которым подравнивались звуки, а квад-

У________________ _.

S0 АО 50 ЬО Ю 80 90

Рис. 3. Функция равных ощущений, соотнося­щая вибрацию (частота 60 Гц), подаваемую на кон­чик пальца, с интенсивностью полосы шума. Наблю­датели подгоняли громкость так, чтобы она соответ­ствовала вибрации (кружки) и чтобы вибрация со­ответствовала громкости (квадратики). Значения раз­дражений даны по логарифмической шкале (в деци­белах). Абсцисса - шум; ордината - амплитуда виб­рации

С. Стивене

МЕТОДЫ ШКАЛИРОВАНИЯ ОТНОШЕНИЙ *

Прежде, чем рассматривать конкретные приме­ры шкал отношений, коротко познакомимся с про­блемой метода или процедуры. Методы создания шкал отношений субъективной величины относи­тельно новы. Правда, Меркель в своей работе "Ме­тоды дополнительного раздражения" (1888г.) пытался найти стимулы, которые удваивали бы кажущееся ощущение, но его изыскания почти не оказали вли­яние на развитие психофизики. Фаллертон и Кэт-телл, используя метод удвоения и деления пополам, не достигли большего. Даже Титченер в своей обсто­ятельной книге "Руководство экспериментатору" ог­раничивается мимолетной ссылкой на метод Мер-келя, т. е. метод "удвоения" стимулов. Об авторе этого метода он говорит: "Мы помним, что он по своему умственному предрасположению является более фи­зиком, чем психологом, и его работа бедна интро­спективными данными". Может быть, Титченер и прав, объясняя недостатки Меркеля "умственным предрасположением". Однако, хотелось бы знать, что бы он сказал, узнав, что, по крайней мере семь раз­личных физических лабораторий внесли важный вклад в разработку шкалы отношений субъективной громкости — шкалы сонов — против, возможно, трех психологических лабораторий.

Толчок к разработке метода — это целая пробле­ма. Сам метод, сколь бы блистательным и перспек­тивным он ни был, немного стоит, если за ним не стоит методология. Физики и психологи разрабаты­вают утонченные методы измерения громкости глав­ным образом потому, что разработка этой пробле­мы представляет для них практический интерес, в особенности для инженеров-акустиков. Это видно уже из того факта, что некоторые из самых ранних работ оплачены коммерческими компаниями. Довольно любопытно, что практическая проблема возникла из-за очевидных недостатков закона Фехнера. Вскоре после принятия децибельной шкалы для измерения интенсивности звука инженеры заметили, что рав­ные деления на логарифмической децибельной шкале не "ведут" себя как равные: уровень 50 дБ выше по­рога совсем не звучит как половина 100 дЪ как это следует из закона Фехнера. Поскольку инженер-аку­стик часто должен объяснять своим заказчикам зна­чение эзотерических акустических измерений, ста­ло очевидным, что требуется шкала, на которой числа должны быть пропорциональны громкости, воспринимаемой рядовым слушателем. Маловероят­но, чтобы без этих практических нужд была пред­принята разработка шкал отношений для 14 перцеп­тивных континуумов, которые мы будем рассматри­вать. Как субъективная шкала отношений, однажды появившись, могла быть положена в основу рабо­ты? Это показано нами, так мы использовали шкалу сонов при разработке метода оценки громкости слож-

* Проблемы и методы психофизики / Под ред. А.Г.Асмолова, М.Б.Михалевской. М.: Йзд-во Моск. ун-та, 1974. С. 71-76.

ного шума из спектрального анализа звука.

Методы построения шкал отношений все еще развиваются, но все они в той или иной форме тре­буют от субъекта количественных оценок субъектив­ных впечатлений. Многие авторы уверяли, что это бессмыслица и ерунда. Однако психологи, придер­живающиеся этих методов, все же идут вперед. Эти прямые оценки ощущения, по-видимому, переста­ли выглядеть бессмыслицей, особенно после того, как они были получены.

В настоящее время в принципе существуют 4 ме­тода, но у каждого из них есть различные варианты. Мы можем классифицировать более или менее сис­тематически эти методы следующим образом.

1. Оценка отношения:

а) прямые измерения отношений;

б) "постоянная сумма".

2. Установление отношений:

а) деление (фракционирование);

б) умножение (мультипликация).

3. Оценка величины:

а) заданный модуль (заданный масштаб, мера);

б) без модуля (не обозначен масштаб).

4. Установление величины.

Я уверен, что во многих психологических иссле­дованиях царит еще больший терминологический хаос, чем в наименованиях психофизических методов и, к сожалению, не вижу радикального средства, которое бы позволило избавиться от великого множества оп­ределений при разработке этих методов. Лучшее, что мы можем сделать — это время от времени вносить некоторую систематизацию. Внеся сначала свою долю в путаницу, я затем попытался внести некоторый порядок в приведенный выше список.

Частично благодаря моим усилиям, второй класс методов, который появился в истории первым, по­лучил название фракционирования, так как обыч­ная процедура метода требует от испытуемого, что­бы он установил (выбрал) стимул для получения ощущения, оцениваемого как половина ощущения, вызванного стандартным стимулом. Другие дроби также используются и дают содержательные резуль­таты. Фракционирование в этом смысле является только частью более общего метода. Другая часть, которую можно назвать умножением, или мульти­пликацией, включает в себя дополнительную проце­дуру, требующую, чтобы испытуемый идентифици­ровал или установил предписанное отношение, ко­торое больше единицы, т.е. переменный стимул в два, три и т.д. раза больше заданного стандарта. Эта процедура использовалась, вероятно, не так часто, как следовало бы; в пользу этого есть достаточно ос­нований, показывающих, что применение процеду­ры удвоения в качестве дополнительной к делению пополам дает возможность сбалансировать опреде­ленные систематические отклонения.

Эти две процедуры вместе могут быть названы установлением отношения. Установление отношений может осуществляться различными способами. Так, экспериментатор может разрешить испытуемому ре­гулировать стимул для того, чтобы получить предпи­санное отношение к стандарту, или же эксперимен­татор может сам установить стимул и спросить ис-

пытуемого, имеет ли место предписанное отноше­ние (метод "постоянных стимулов").

Интересный вариант установления отношений включает фиксацию двух яркостей для того, чтобы определить кажущееся отношение, которое испыту­емый должен воспроизвести, устанавливая две гром­кости в том же самом кажущемся отношении, В экс­перименте, проведенном Дж. Стивенсом, физичес­кое отношение (децибелы), устанавливаемое испы­туемыми между интенсивностями белого шума, при­близительно совпадает с отношением, которое экс­периментатор устанавливает между интенсивностя­ми двух белых поверхностей. <...>

Метод оценки отношения обратен по процедуре методу установления отношения. Вместо того, что­бы задать отношения заранее, экспериментатор по­дает два (или более) стимула и просит испытуемого назвать отношения между ними. Испытуемый может дать прямую оценку отношений, как и в первых опы­тах Ричардсона и Росса, или он вынужден будет вы­разить отношение при помощи деления заданного числа точек на две группы, пропорциональные двум стимулам по способу, предложенному Метфесселем. Принуждение, включенное в так называемый метод "постоянной суммы", содержит очевидные недостат­ки, которые проявляются при работе с большим ди­апазоном отношений.

Метод оценки величины имеет дело с отношения­ми как таковыми и требует, чтобы испытуемый при­писал числа последовательности стимулов при ин­струкции выбирать числа, пропорциональные вос­принимаемым величинам ощущений. Эксперимен­татор может задать меру (модуль) предъявлением некоторого стимула и дать ему некоторое особое зна­чение, например, 10, или он может представить ис­пытуемому возможность самому свободно выбрать свой модуль. (Замечание: если оценка величины дает асимметричное распределение, как обычно бывает, то желательно подсчитывать медианы вместо сред­них арифметических).

Метод оценки величины является логически об­ратным методу установки величины', этим методом больше всего пренебрегали. Вместо предъявления серии стимулов в случайном порядке и вместо того, чтобы просить испытуемого оценить их восприни­маемые величины, экспериментатор может назвать различные величины и попросить испытуемого от­регулировать стимулы таким образом, чтобы они были пропорциональны субъективным величинам. Подобно любому методу, он имеет, вероятно, свои достоинства и свои недостатки, и интересно выяс­нить величины, по крайней мере, некоторых из них.

Одно мы знаем точно - это то, что при использо­вании этого метода экспериментатор должен сопро­тивляться любому импульсу, который побуждал бы его обозначить верх или низ диапазона. В противном случае эта задача превращается в одну из задач кате­гориального шкалирования. В некоторых более ранних экспериментах мы использовали подобный метод, который можно назвать установлением категорий, чтобы получить семиточечную шкалу категорий для громкости. Мы предъявляли два уровня, которые обо­значались как 1 и 7, а затем просили испытуемых вос­производить в случайном порядке остальные катего­рии. Результаты были подобны обычным оценкам ка­тегорий, полученным для континуума класса 1: фун­кция была выпукла вниз, когда график вычерчивался против шкалы сонов (по оси абсцисс).

Установление величины производилось в экспе­рименте, в котором для обозначения величины мы предпочитали яркость, а не число. Мы устанавлива­ли яркость одного тест-объекта на разных уровнях и просили испытуемых отрегулировать шум таким об­разом, чтобы его громкость казалась столь же силь­ной, как и яркость света. Хотя это исследование (про­водимое Дж. Стивенсом) еще не закончено, резуль­таты, по-видимому, вполне соответствуют тому, что мы знаем относительно субъективных шкал для гром­кости и яркости. Интенсивности белого шума про­порциональны в грубом приближении интенсивно-стям белого света, что явно предполагает, что гром­кость и яркость являются сходными функциями ин­тенсивности.

Все четыре метода дают необходимые данные для построения шкалы отношений. Каждый метод мо­жет быть изменен и модифицирован множеством различных способов. Нужно не только изменять и адаптировать методы для успешного разрешения кон­кретной проблемы, но и в любой серьезной попыт­ке создания определенной шкалы для заданного пер­цептивного континуума требуется искать возможные источники отклонений, смещений и искажений, используя разные методы и различные значимые параметры. В настоящее время валидная шкала, ко­торая представляет типичного испытуемого, едва ли может быть получена с первой попытки.

Описанные ниже шкалы отношений созданы с помощью одной или более из перечисленных выше основных процедур. Не все они были подвергнуты интенсивному исследованию и перекрестной про­верке, как того заслуживают, но мы заинтересова­ны скорее в получении их общего вида, а не деталей. В первом приближении все они являются степенны­ми функциями.

Р.Вудвортс, Г.Шлосберг

МЕТОДЫ ШКАЛИРОВАНИЯ *

Метод равных сенсорных расстояний

Имеется ряд методов, в которых испытуемый пытается выбрать или согласовать серию стимулов так, чтобы они отмечали субъективно равные рас­стояния на некотором континууме. Первый из них — "деление интервала пополам" — был использован Плато в 1850г. Он просил художников воссоздать се­рый тон, который является средним между черным и белым. Иными словами, субъективное расстояние между белым и серым было таким же, как между черным и серым. Метод разработан Дельбефом, Мюл­лером и Титченером (1905). Основной целью была проверка справедливости закона Фехнера. Если бы средняя точка совпадала со средним геометричес­ким, а не средним арифметическим, то Фехнер ока­зался бы прав. Иногда точка приходилась на одно среднее, иногда на другое; случалось и так, что она оказывалась где-то между ними. Мы не будем рас­сматривать старые доказательства, которым Титче-нер посвятил целый раздел своей книги. Понятно, что этот метод подвержен тем же ошибкам, что и метод фракционирования. В самом деле, метод деле­ния интервала пополам очень похож на метод деле­ния пополам величины. Единственным различием является то, что метод деления пополам может да­вать истинный нуль для шкалы.

Эксперимент Сенфорда. Конечно, нет причины ограничивать эксперименты делением пополам. Мож­но раздробить субъективное расстояние на любое количество равных интервалов. В эксперименте по взвешиванию Сенфорда 108 пакетов, ранжирован­ных от 5 до 100 г, раскладываются на пять кучек с приблизительно равными сенсорными расстояния­ми между ними. Если среднее от всех весов, поме­щенных в каждую кучку, нанести на ординату в ло­гарифмическом масштабе, а субъективные величи­ны в линейном масштабе — на абсциссу, то по зако­ну Фехнера точки должны лечь на прямой линии. <...>

Парное сравнение

Существуют, по крайней мере, два метода шка­лирования — шкалирование отношений возвращает к работе Фехнера - пионера в области эксперимен­тальной эстетики и его методу выбора. Этот устарев­ший метод был использован Фехнером при изуче­нии эстетической оценки различных вариантов пря­моугольников. Он изготавливал картонные ящички, стороны которых изменялись в пределах от квадрата

" Проблемы и методы психофизики / Под ред. А.Г.Асмолова, М.Б.Михалевской. М.: Изд-воМоск. ун-та, 1974. С. 193-194, 202-204,208-211.

до узкого прямоугольника и разбрасывал их в слу­чайном порядке на столе. Фехнер проводил экспе­римент с несколькими сотнями людей, предлагая каждому выбрать наиболее и наименее приятные формы фигурок, разбросанных на столе. Затем он мог использовать относительную частоту выбора в каче­стве показателя и таким способом определял эсте­тическую ценность каждого прямоугольника. Благо­приятные выборы падают, в основном, на середину серии (около золотой серединки), а неблагоприятные - в экстремальных направлениях.

Две наиболее совершенные формы выбора изве­стны как метод ранжирования и метод парных срав­нений. Если бы Фехнер попросил распределить все приятные прямоугольники в одном конце, а непри­ятные — в другом, то такое категоричное распоря­жение дало бы больше дополнительной информа­ции. Если бы показывал он только два прямоуголь­ника одновременно и просил бы испытуемого выб­рать наиболее приятный, то, проделывая то же са­мое со всеми парами, Фехнер опять-таки мог бы по­лучить больше информации, чем методом выбора. Или он мог бы взять определенный прямоугольник в качестве стандарта. Предъявляя стандарт в паре со сравниваемыми, он получил бы оценку сравнивае­мого как более или менее приятного, чем стандарт­ный, подобно тому, как это делается методом по­стоянных раздражителей. Это последнее предполо­жение недостаточно обосновано психологически в изучении эстетических или других величин потому, что испытуемый как бы пресыщается стандартными стимулами. Однако, мы увидим, что с точки зрения логики и математики метод парных сравнений явля­ется сокращенным методом постоянных раздражи­телей. Кроме того, метод ранжирования сводится к методу парных сравнений.

Метод парных сравнений введен Коном при изу­чении предпочитаемое™ цветов. Его часто призна­ют в качестве наиболее адекватного способа получе­ния надежных оценок. Задача испытуемого в любой момент упрощается до предела, потому что перед ним только два образца. Он сравнивает их в опреде­ленном отношении, переходит к другой паре и так до тех пор, пока не оценит всех образцов. Если каж­дый образец сочетается с каждым другим, то коли-

и(я-1)

чество пар равно —^— , что составляет 45 пар из 10 образцов или 190 из 20. "Работа" может иногда сокращаться: можно разделить серию образцов на две или более частных серий. Предъявляя все пары сти­мулов в случайной последовательности, эксперимен­татор может избавиться от временной и простран­ственной ошибок, помещая каждый образец первым в одной паре и вторым в другой. В индивидуальных экспериментах он может приготовить бланк регист­рации в форме таблицы (см. табл. 1). Каждый образец представлен в строчке и колонке. Если, например, испытуемый предпочитает G букве В, то буква G записывается на пересечении колонки G и строчки В. Когда все выборы уже сделаны, экспериментатор подсчитывает все G, занесенные в таблицу в строч­ке G или колонке С и записывает количества под колонкой G. Таким образом, экспериментатор узна­ет частоты выборов (С-частоты). Когда перед на­блюдателем 10 образцов, каждый сравнивается с

оставшимися девятью; чтобы получить процентное или вероятностное выражение, каждое значение С делится на 9 или в общем виде на («—1). Возможна определенная проверка: сумма показателей С-час-

тот должна быть равна OiO^A _t средняя величина р должна быть равна 0,50.

Тшблица 1 Парные сравнения, форма записи

Н I J

Образцы ABC

В В J

С Е

С D Е

С D Е F

В В

С J Е F G J J

С D Е F G

С D Е I G I

С D Е F G Н I J

С-частоты

Метод ранжирования

Другое название этого метода — метод качествен­ного упорядочивания. Оно говорит само за себя; испы­туемый упорядочивает по данному признаку предъяв­ленное число образцов. Так получают один ранго­вый порядок. Одни и те же образцы упорядочивают­ся несколько раз, обычно разными наблюдателями и для каждого образца подсчитывается средний ранг. Этот метод очень удобен, когда мы имеем дело с большим количеством образцов. Обычно несколько образцов предъявляют одновременно и позволяют испытуемому выбирать один ранговый порядок так долго, как он пожелает. Когда много образцов, его могут попросить грубо рассортировать их по каче­ствам (классам) до того, как он приступит к окон­чательному ранжированию.

Одной из первых работ, связанных с методом ранжирования, была работа Кэттелла с уточнения­ми и дополнениями его учеников (Самнера, Торн-дайка, Уэллса, Стронга, Холлингворта). Тем време­нем Спирман показал, как использовать порядко­вые ряды при измерениях корреляции - важный вклад в метод.

Кэттелл воспользовался методом ранжирования для определения лидеров любой естественной науки в оценке их коллег. Он предложил 10 психологам проранжировать 200 американцев, которые претен­довали на звание психолога, десять судей работали самостоятельно, независимо друг от друга. Затем Кэттелл подсчитал среднее всех 10 рангов, опреде­ленных для каждого психолога. Он опубликовал пе­речень самых высоких средних рангов в 1903 г. и от­крыл имена людей в 1933 г. Наша таблица включает в себя 51 имя и их порядок. Некоторые из людей были скорее философами, чем психологами; неко­торые лица, стоящие вблизи или на некотором рас­стоянии от конца таблицы, были молодыми людь­ми, которых еще рано было посвящать в рыцари. Что касается значимости такого списка, то мы не мо­жем сделать ничего лучшего, чем привести цитату из оригинала — статьи Кэттелла: "Следует четко от-

метить, что эти оценки дают только то, что они от­крыто могут дать, а именно, результирующее мне­ние 10 компетентных судей. Они показывают репу­тацию человека у экспертов, но совсем не обяза­тельно его способности или вклад (в науку). Не ис­ключены постоянные ошибки, которые происходят из-за того, что он известен больше или меньше. Одна­ко нет других критериев для оценки деятельности человека помимо той, которая получена от большин­ства компетентных судей".

Мы имеем здесь нечто подобное нормальному распределению; мы имеем только верхнюю четверть такого распределения, четверть, которая сама явля­ется выделенной группой женщин и мужчин, уже получивших степень и положение учителя. Мы не можем использовать эти данные для создания шка­лы превосходства или репутации, имеющей в осно­вании абсолютный нуль. Мы можем несколько улуч­шить шкалу, взяв человека, занявшего верхнее мес­то на шкале в качестве отсчетной точки и спросить, кто вдвое менее хорош, чем Вильям Джемс. Но это будет уже другой эксперимент. Что можно получить от средних рангов кроме их положения?

Средние ранги ведущих американских психологов 1903 года

(Кэттелл, 1903, 1933)

1.0. Вильям Джемс

3.7. Дж. Мак Кин Кэттелл

4.1. Хьюго Мюнстерберг

4.4. Г. Стенли Халл

7.4. Дж. Марк Болдуин

7.5. Эдвард Б. Титченер

7.6. Ионна Ройс

9.2. Георг Т.Лэдд
9.6. Джон Девэй

11.6. Иозеф Ястров
12.3. Эдмонд К. Сэнфорд

16.8. Мэри В. Калкинс
17.1. Вильям Л. Бриан

17.8. Георг С. Фаллертон

18.7. Георг М. Страттон

19.3. Эдвард Л. Торндайк
19.6. Эдмонд В. Делабарре

21.6. Эдвард В. Скрипчер

21.8. Христина Лэрд-Франклин

22.4. Генри Ратчерс Маршалл

24.4. Чарльз X. Джадд

27.0. Джеймс Р. Энгелл
29.5. Лайтнер Виттер

37.5. Г. Т. Патрик

37.7. Говард Уоррен

40.4. Вильям Т. Харрис

41.6. Раймонд Додж

42.9. Джеймс X. Хизлон

44.7. Карл Сишор
44.9. Чарльз Стронг

45.5. Артур X. Пирс

46.4. Роберт Мак Доугалл

47.1. Макс Мейер
48.0. Эрнст X. Линдлей
49.3. Джеймс Лейба

49.6. Фрэнк Энгелл
49.9. Вальтер Пилльбери

51.1. Вильям Р. Ньюболд
52.6. Ливингстон Фарранд
53.3. Герберт Никольс
54.5. Якоб Г. Шурман
54.5. Маргарет Ф. Уошборп

56.1. Роберт С. Вудвортс

56.2. Шеферд И. Франц

56.5. Харри К. Во<