Типы шкал. Косвенное измерение ощущений. Пороги ощущений. Чувствительность. Методы измерения порогов.

Закон Фехнера

П. О.Макаров

ОБ ОСНОВНОМ ПСИХОФИЗИЧЕСКОМ ЗАКОНЕ *

Два столетия назад, в 1760 г., Бугер исследовал свою способность различать тень, отбрасываемую свечой, если экран, на который падает тень, одно­временно освещается другой свечой. Его измерения довольно точно установили, что отношение Д/// (Д/ - минимальный воспринимаемый прирост освеще­ния, / - исходное освещение) — величина сравни­тельно постоянная в отличие от абсолютных вели­чин Д/. В 1834 г. Э. Вебер повторил забытые к тому времени опыты Бугера. Изучая различение веса, он показал, что минимально воспринимаемая разница в весе представляет собой постоянную величину, равную приблизительно ¹/_ш, т. е. груз в 31 г различа­ется от груза в 30 г; груз в 62 г от груза в 60 г; в 124 г от 120 г и т. д. Такое же постоянство в отношении минимального воспринимаемого прироста раздраже­ния к его исходной величине Вебер установил для зрения (различение длины линий) и слуха (различе­ние высоты тона). Вебер предполагал, что им обна­ружен важный общий принцип, однако специаль­ного закона он не сформулировал.

Выражение "закон Вебера" принадлежит Фехне-ру, но впоследствии укоренилось выражение "закон Вебера-Фехнера", так как роль Фехнера в разработ­ке проблемы измерения ощущений исключительно велика. Фехнер рассуждал следующим образом. Мы не можем измерить ощущение. Мы можем только удо­стоверить, есть ли ощущение, больше, меньше или равно данное ощущение другому. Но поскольку мы можем измерять стимулы, мы можем измерить и минимальный стимул, необходимый для вызова ощущения или для того, чтобы минимально усилить или минимально ослабить имеющееся в наличии ощущение. Поступая таким образом, мы измеряем чувствительность как величину, обратную порогу. Фехнер ввел понятие об абсолютной и различитель­ной (или дифференциальной, или разностной) чув-

* Хрестоматия по ощущению и восприятию / Под ред. Ю.Б.Гиппенрейтер, М.Б.Михалевской. М.: Изд-во Моск. ун-та, 1975. С. 249-252.

ствительности: абсолютная чувствительность изме­ряется абсолютным порогом, т.е. минимальной ин­тенсивностью раздражения, вызывающей ощущение, различительная чувствительность измеряется разност­ным порогом, т.е. минимальным приростом интен­сивности раздражения, вызывающим усиление или ослабление ощущения, по отношению к исходной интенсивности раздражения. Так, если груз в 60 г (I) оценивается как равный по весу грузу в 61 г и чуть более легкий, чем груз в 62 г (/,), то минимальный воспринимаемый прирост веса будет равен:

Д/ = /,-/ = 62 - 60 = 2 г,

а разностный порог (отношение Вебера) будет
равен: д. . .

Т⁼бо ⁼ зо'

Закон Вебера выражается, таким образом, фор­
мулой: дд

—-= константа (1)

к

для едва воспринимаемого прироста величины
раздражения R. ._

Фехнер предположил, что если — = константа,

R

то и минимальный прирост ощущения (AS) относи­тельно исходного уровня ощущения (S) тоже кон­станта, т. е.

_AS = c— - (2)

R

где с — константа пропорциональности. Формула (2) — это "основная формула Фехнера". Введение AS в уравнение (2) следует рассматривать как заключе­ние Фехнера о равенстве между собой всех AS, всех минимальных приростов ощущения. Таким образом, приросты ощущения AS рассматриваются Фехнером как единицы измерения. Интегрируя уравнение (2), Фехнер получил

S=clog_cR+C, (3)

где С — константа интегрирования, ас - осно­вание натуральных логарифмов. С помощью этой формулы, зная обе константы с и С, можно вычис­лить величину ощущения для стимула любой интен­сивности. Однако поскольку константы неизвестны, эта формула неудовлетворительна, и Фехнер заме­нил С, сделав допущение о нулевой величине S при пороговой величине R. При R — г, т.е. при величине раздражения, равной абсолютному порогу, S = 0.

Подставляя значения R и S при R = г в формулу (3), получаем

О = clog/+C С= - с log/

Теперь мы можем заменить С в формуле (3): S = с log_e7? - с log/ = c(log_tR - log/) = с log_ei*

Путем соответствующего изменения константы с на к переходят от натуральных логарифмов к деся­тичным, тогда

(4)

S = к log-г

Это и есть Massformel Фехнера — формула для из­мерения ощущений. Шкала S — это шкала едва разли­чимых приростов ощущения над нулем, т. е. ощуще­нием при абсолютном пороге. Затем Фехнер сделал еще одно допущение. Он предположил, что мы мо­жем измерять R, любой надпороговый стимул, его отношением к г, пороговому стимулу. Если, таким образом, принять г за единицу измерения, г = 1, то

S = к log/? (5)

Этой последней формуле (5) Фехнер и дал на­звание "закона Вебера". Выраженная словами, она гласит: величина ощущения пропорциональна лога­рифму величины раздражения. Разумеется, закон Вебера выражается формулой (1), а не формулой (5). Формула (5) выведена, как мы видели, при ряде ус­ловных допущений: во-первых, что единицей R яв­ляется пороговая величина стимула г, во-вторых, что S = О при пороге, т. е. при R = г, в-третьих, что все DS, все минимальные воспринимаемые приросты ве­личины раздражения, равны между собой. Прежде всего формула (5) требует соблюдения формулы (1), а между тем последующие эксперименты показали, что отношение Вебера постоянно не во всем диапа­зоне интенсивностей раздражения. Тем не менее, не­смотря на бесчисленную критику и все ограниче­ния, закон Бугера—Вебера—Фехнера имеет достаточ-

но широкую зону приложения. Существенно, что формула Фехнера (5) приложима к деятельности некоторых изолированных рецепторов. В определен­ном диапазоне интенсивностей частота токов дей­ствия есть линейная функция логарифма интенсив­ности. Это показано на мышечном веретене Мэтью-сом (1931) и на глазу Limulus Хартлайном и Грэмом (1932). Разумеется, здесь приходится говорит не об 5-ощущении, а об Е-возбуждении:

Е = к log R

Фехнер соединял в себе физика, психофизио­лога и философа-идеалиста. Отвергая его идеалисти­ческие построения, мы должны признать, что как физик он внес в физиологию органов чувств чело­века новые точнейшие методы количественного из­мерения отношения стимул — ответ. Это, во-первых, уже описанный нами метод измерения едва разли­чимых приростов величины раздражения, позже на­званный методом пределов, во-вторых, метод проб и ошибок, позже названный методом постоянного стимула (исследуемый сравнивает целый ряд стиму­лов с одним и тем же постоянным стимулом по ка­кому-нибудь признаку — больше или меньше, тем­нее или светлее, длиннее или короче и т.д.), и, в-третьих, метод средней ошибки (исследуемый сам подбирает стимул, равный заданному или в то или иное число раз больший или меньший заданного). Фехнер установил значение изменчивости при "пси­хофизических", как он выражался, измерениях, не­обходимость определения средних и крайних вели­чин и законы изменчивости средних величин, т.е. ус­тановил необходимость статистических методов.

Фехнер считается одним из основателей экспе­риментальной психологии, а физиологи вправе ска­зать, что он развил открытие Бугера-Вебера в за­кон — метод измерения различительной чувствитель­ности органов чувств и, таким образом, заложил основы измерения нервных процессов у человека с помощью варьирования и точного измерения нано­симых раздражений.

Ф.А.Джелдард

СЕНСОРНЫЕ ШКАЛЫ *

Работы Вебера, Фехнера, а с тех пор и многих других были направлены на достижение первой цели науки - измерения. Однако система знания остается не до конца продуманной и недостаточно опреде­ленной до тех пор, пока неправильно применяется математика, пока не используются те богатые возможности, которые дает описание основных ис­следуемых соотношений в количественных поняти­ях. Если научные феномены выразить в числах, то мы получим шкалы того или иного вида.

Науке известно три различных вида измеритель­ных шкал, и все они применяются в психологии. Это шкалы порядка, интервалов и отношений. Рассмотрим конструкцию и цели каждой из этих шкал.

Шкала порядка указывает только порядок явле­ний по степени выраженности того или иного при­знака. Коллекцию камней, карандашей или фотопле­нок, по-разному экспонированных, можно размес­тить на порядковой шкале, раскладывая их по весу, длине или серости. Самый длинный, тяжелый и тем­ный обозначается номером один, следующий за ним по порядку — два, следующий за вторым — три и т. д. В результате этой процедуры мы получим шкалы порядка. Столь же произвольно мы можем присво­ить номер 1 самому легкому камню, номер 2 — кам­ню потяжелее и т. д. Многие "сырые" (грубые) шка­лы имеют такую конструкцию. Некоторые из них, имеющие определенное научное и практическое при­менение, построены таким образом или происходят именно от этой процедуры упорядочения. Известно, например, что шкала твердости используется в гео­логии и технике. Сейчас твердость измеряется по шкале интервалов, а первоначально — по шкале по­рядка. Наиболее твердый минерал в мире — алмаз, занимает место на верхнем конце шкалы, а самый мягкий - тальк - на нижнем крае шкалы. Почему? Дело в "способности царапать". Алмаз может делать царапину на корунде, топазе или кварце; конечно, при соответствующих условиях можно сделать цара­пину на любом материале. В то же время ни один из них не может поцарапать алмаз.

Недостаток шкал порядка состоит в том, что они ничего не говорят нам о расстояниях, разделя­ющих разные точки на шкале. Насколько алмаз твер­же кварца, гипса или талька? Исходная шкала по­рядка ничего не может сообщить по этому поводу, поскольку все шкалы порядка не отвечают на такие вопросы. Хотя на шкале твердости алмаз помечен № 10, корунд - № 9, а тальк - № 1, по ряду со­ображений расстояние между алмазом и корундом считается большим, чем между корундом и таль­ком. Измеряя силу ощущения по шкале порядка, получить которую намного легче, чем другие шка­лы, мы не можем ожидать, что эта шкала даст нам возможность сказать, насколько одно ощущение сильнее другого. Мы увидим только, что оно силь-

* Хрестоматия по ощущению и восприятию / Под ред. Ю.Б.Гиппенрейтер, М.Б.Михалевской. М.: Изд-во Моск. ун-та, 1975. С. 253-261.

нее, если оно имеет более высокое порядковое зна­чение или ранг.

Чтобы получать более полезные результаты из­мерения, мы должны найти способ применять в шкалировании скорее количество, чем порядок. Нуж­но изобрести единицу измерения. Это сделано на шкале интервалов, которая дает нам возможность определить разницу между двумя точками на ней.

Шкала, применяемая на всех обычных термомет­рах, является шкалой интервалов независимо от того, выражена ли она в градусах по Фаренгейту или по Цельсию. В обоих случаях интервал, скажем Г, явля­ется одним и тем же во всех частях шкалы. Нет боль­ших или малых градусов. Шкала имеет постоянный интервал. Очевидно, что и шкала Фаренгейта и 100-градусная шкала имеют только произвольно выбран­ный нуль. Эта особенность не позволяет шкале ин­тервалов стать более полезной, чем она есть на са­мом деле. Немецкий физик Г. Д. Фаренгейт взял смесь снега и соли и эту температуру принял за нуль. В ка­честве второй фиксированной точки 12 была перво­начально выбрана температура человеческого тела. Позднее ее заменили на 96, что позволило сделать эту шкалу более дробной (тонкой). Точка замерза­ния воды стала равна 32*, а точка ее кипения при нормальном атмосферном давлении поднялась до 212°. Равные интервалы температуры были выбраны им очень просто: он пометил на стеклянной трубочке объемы расширения ртути или спирта. Собственно, шкала Фаренгейта получает привязку на верхнем конце в точке парообразования, 212"; температура тела поднялась на 2—3" по сравнению с прежней и сейчас принята равной 92,6°. Стоградусная шкала, наиболее часто употребляемая в науке, построена по той же логике, но численно является более про­стой. За нуль принята точка замерзания воды, за 100° — точка кипения воды.

Обе шкалы обладают особенностями всех шкал интервалов независимо от их длины. Однако сравни­вать температуры можно только через их разности на данной шкале, поскольку нулевая точка на лю­бой шкале интервалов не имеет существенного зна­чения. Нельзя сказать, что 40° вдвое теплее 20' неза­висимо от того, измерены эти температуры по шка­ле Фаренгейта или Цельсия; напротив, высказыва­ние типа: "Две измеренные температуры различают­ся на 20 единиц шкалы", конечно, имеет смысл, его можно выразить в единицах шкалы Цельсия или Фа­ренгейта.

Шкалы отношений встречаются во всех облас­тях науки, они представляют и самые простые изме­рения, и наиболее изощренные. Общие измерения длины, веса, электрического сопротивления, ско­рости и плотности осуществляются по шкале отно­шений. Здесь существуют действительные нулевые точки. "Нулевая длина", "нулевой вес", "нулевая ско­рость" понятны для всех. Отнимите 1 дюйм из 1 дюй­ма, 5 фунтов из 5 фунтов и 10 миль/ч из 10 миль/ч, и не будет никаких сомнений в результатах. Также не возникает сомнений, что 10 миль/ч — это дважды по 5 миль/ч и что I дюйм — это '/₁₂ фута. Существование равных единиц и действительной нулевой точки де­лает возможным сравнение отношений. В этом и зак­лючается большое достоинство шкал отношений.

Если мы хотим точно охарактеризовать стиму­лы, то чаще всего пользуемся шкалой отношений — шкалой размера, веса, яркости и т. д. Но что можно сказать об ощущениях, вызываемых этими стимула­ми? Можно ли шкалировать ощущения? Да, если возможны "ощущаемые отношения". Что подразуме­вается под этим и как мы переходим от ощущений к шкале отношений?

Существует несколько способов шкалирования, главными среди них являются фракционирование, оцен­ка отношения и оценка величины. Иногда все три ме­тода дают приблизительно одни и те же результаты, и тем самым подтверждают друг друга.

При методе фракционирования испытуемому предъявляется эталон (стандарт) определенной ин­тенсивности, который он должен сравнить с рядом слабых стимулов, пытаясь выбрать один, который, как ему кажется, составляет простое отношение (дробь) с эталоном (обычно равен половине этало­на). Допустим, что строится шкала отношений для громкости звука. Испытуемому предъявляют тон по­стоянной интенсивности и предлагают подобрать более тихий тон так, чтобы его громкость была рав­на половине громкости эталона. Эта процедура по­вторяется на разных уровнях интенсивности в ши­роком диапазоне. Установки испытуемого представ­ляют собой большое число интервалов, каждый из которых оценивается как отношение 1:2. С их помо­щью можно построить шкалу. Это будет шкала отно­шений, которая содержит истинный нуль.

Какой вид будет иметь такая шкала, если ее по­местить вдоль шкалы физической интенсивности? Ответ можно получить, рассмотрев рис.1. Громкость - мера силы звукового ощущения, представлена в зависимости от интенсивности стимула в децибелах (см. подпись к рис. 1). Увеличение оценки громкости по мере увеличения интенсивности стимула изобра­жено сплошной линией, названной "шкалой сонов". Сон - единицы громкости. Один сон — громкость тона, частота которого равна 1000 Гц, а интенсив­ность — 40 децибелам над абсолютным порогом. Два сона равны удвоенной громкости, три сона - утро­енной громкости и т. д. Крутой участок кривой озна­чает, что при высоких интенсивностях звука гром­кость возрастает быстрее. По определению, один сон получают при тоне 40 децибел. Видно, что 2 сона имеют место при тоне 55, 7 сонов — при 60, 13 со­нов - при 70, 25 сонов - при 80, 50 сонов — при 90 децибелах над абсолютным порогом. При низких уров­нях интенсивности звука мы должны сильно про­двинуться по нашей логарифмической шкале физи­ческой энергии, чтобы получить незначительное возрастание громкости, но при высоких интенсив­ностях сравнительно небольшое увеличение энергии ведет к громадному изменению громкости. Указан­ные выше соотношения получены эмпирически в результате тщательных экспериментов. Для упроще­ния расчетов громкости было принято международ­ное соглашение о том, что увеличение интенсивно­сти на 10 децибел удваивает громкость. Итак, гром­кость звука, интенсивность которого равна 40 деци­бел, составляет 1 сон; 50 децибел - 2; 60 децибел -4; 70 децибел - 8 и т. д.

Прерывистая линия (рис. 1), названная "шкалой децибел", показывает, как увеличилась бы громкость,

если бы выполнялся закон Фехнера, так как на го­ризонтальной оси отложены логарифмические еди­ницы — децибел тоже является логарифмической единицей — интенсивность ощущения должна быть связана с ней линейно. Ясно видно большое расхож­дение между предсказаниями закона Фехнера и ре­зультатами измерений по методу фракционирования. Второй метод - оценка отношения - связан с методом фракционирования и поэтому может слу­жить проверкой для него. Метод оценки отношения состоит в том, что испытуемому предъявляют два различных по интенсивности стимула и просят оце­нить кажущееся отношение между ними, например, составляет ли слабый звук по громкости '/₂, '/₅, ⁴/_s или какую-либо другую часть сильного звука. Такие субъективные оценки возможны, если они не очень затруднительны. В действительности испытуемые вна­чале не очень уверены в правильности оценок, но скоро приобретают способность быстро оценивать отношения, и точность оценок показывает, что они могут служить ценным дополнением к методу фрак­ционирования.

ии			__ |						/
									^£
								j
							А[		/
								/
					А			\1
			/'
			/1							—1
	/
	/				г——	——-

0 20 40 60 80 100 Лес. /. Зависимость громкости от интенсивнос­ти звука:

Ось абсцисс - интенсивность звука в децибелах над абсолютным порогом; ось ординат - громкость в сонах. При низких физических интенсивностях оценка громкости (сплошная линия, названная "шкала в сонах") возрастает медленно, а при высо­ких — быстро. Мера физической интенсивности -децибел определяется как '/,„ log₁₀ EJE_a, где £, -измеряемая акустическая энергия, Е„ - энергия ус­ловного эталона, взятого в качестве точки отсчета (обычно 0,0002 дин/см², что приблизительно соот­ветствует абсолютному слуховому порогу "среднего" молодого человека при частоте тона, равной 1000 Гц). Таким образом, децибелы изменяются по логариф­мическому закону, нулю децибел соответствует ин­тенсивность звука, равная порогу слышимости, 40 децибелам - интенсивность звука в среднем уч­реждении, 60 децибелам — интенсивность голосов во время разговора, 100 децибелам — грохот в ко­тельном цехе, 120 децибелам - удар грома, а рев реактивных двигателей некоторых самолетов может достигать 160 децибел и более. Прерывистая линия, обозначенная как "шкала в децибелах", показывает, какой вид имела бы зависимость между громкостью и физической интенсивностью, если бы выполнялся закон Фехнера, так как громкость дана в линейном масштабе, меняется по линейному закону, а интен­сивность (децибелы) — по логарифмическому (Вуд-вортс и Шлосберг, 1954. С. 239)

40 60 80 tOO

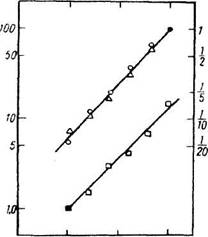
Рис. 2. Сенсорные величины, полученные дву­мя методами на одной и той же группе испытуемых: Абсцисса — уровень звукового давления в деци­белах. Верхняя прямая показывает оценку громкос­ти, полученную методом оценки величины (левая ордината), и методом оценки отношения (правая ордината). Нижняя прямая показывает хорошее со­ответствие данных той же степенной функции (на­клоны прямых точно совпадают), когда вместо мо­дуля 100, использовавшегося в эксперименте, был выбран модуль 1. Кружочками и квадратиками обо­значены результаты оценки величины, треугольни­ками - результаты оценки отношения, (по С.С.Сти-венсу II Американский журнал психологии. 1956. Т. 59. С. 19)

Частным случаем метода оценки отношения яв­ляется метод постоянной суммы. Два стимула, раз­личные по интенсивности (или по другой характе­ристике), предъявляются одновременно или непос­редственно один за другим, и наблюдатель должен оценить каждый в процентах от их суммы. Так, два расположенных рядом световых пятна сначала, ког­да их яркости кажутся различными, могут быть оце­нены как 70 и 30, а затем, по окончании уравнива­ния, как 50 и 50. Очевидно, что метод постоянной суммы есть метод оценки отношения, где оценки даются в процентах. Сказать, что два "слагаемых" в сумме составляют 100, — не значит скрыть существу­ющие между ними отношения (7:3; 1:1).

Если сенсорная величина может быть разделена пополам или на четыре части, как это делается в методе фракционирования, и если могут быть оце­нены отношения между двумя или более впечатле­ниями даже разных модальностей, то можно поста­вить вопрос, не существует ли более прямого спосо­ба оценки сенсорных уровней? Можно ли, напри­мер, отправляясь от некоторой точки, эталона, при­писать числа другим ощущениям? Было предприня­то много попыток решить этот вопрос, и теперь уже ясно не только то, что человек способен с извест­ной точностью прямо оценивать величину ощуще­ния, но и что с помощью метода оценки величины можно получить некоторые важные выводы, касаю­щиеся отношений стимул — ощущение.

В методе оценки величины используется более пря­мая процедура. Предположим, что мы хотим полу­чить прямые оценки величины громкости и тем са-

мым проверить результаты, полученные с помощью метода оценки отношения. Сначала мы предъявляем тон умеренной громкости, например, равный 80 де­цибелам, и сообщаем наблюдателю, что эта гром­кость является эталоном и должна быть оценена, на­пример, 10 единицами (модуль). Испытуемый дол­жен численно оценивать относительную громкость всех последующих предъявляемых тонов, причем более слабым тонам должны быть приписаны числа меньше 10, а более громким — больше 10. Если пере­менный тон в четыре раза громче эталона, ему при­писывается 40, если он кажется вдвое слабее этало­на, ему приписывается 5 и т.д. Экспериментатор не накладывает никаких ограничений на пределы оце­нок на обоих концах шкалы. Затем в случайном по­рядке испытуемому предъявляют большой ряд ин-тенсивностей, выбранных заранее.

Результаты, полученные с помощью такого ме­тода, хорошо соответствуют результатам, полученным с помощью метода оценки отношений. На рис. 2 (верх­няя кривая) показаны результаты решения обеих за­дач группой из 8 испытуемых. В этом опыте для оцен­ки величины использовался максимальный модуль 100 - модуль не обязательно должен иметь "умеренную" интенсивность или быть "центральным" числом, - и испытуемым предъявлялись для численной оценки 5 более слабых и достаточно удаленных друг от друга громкостей. При оценке отношения модуль был равен 1, а знаменатель дроби варьировал в зависимости от интенсивности тона. Нижняя кривая показывает, что во второй задаче была получена та же функция. А имен­но линии, соединяющие точки, имеют такой же на­клон, когда модуль представлен наименьшей интен­сивностью (1,0 для звука в 60 децибел), а все оцени­ваемые интенсивности оказываются выше его.

Возможно, наиболее важным результатом экспе­риментов по оценке величины является вывод, те­перь уже достаточно убедительный, что для некото­рых сенсорных характеристик равные отношения меж­ду стимулами приводят к равным отношениям между ощущениями. Чтобы понять смысл этого утверждения, достаточно взглянуть на рис. 2. Заметим, что на орди­нате отложены значения в логарифмических едини­цах, т. е. расстояния от 1 до 10 равны расстоянию от 10 до 100. Абсцисса также является логарифмической шкалой, так как сам децибел является логарифми­ческой единицей. Если изображенная на графике за­висимость между двумя логарифмическими перемен­ными выражается прямой линией, то мы знаем, что имеем дело со степенной функцией. Такая функция представлена (рис. 2); она была получена при многих других измерениях сенсорных величин. <...>

Все сказанное позволяет заключить, что в пси­хологии, как и в физических науках, мы можем точ­но измерять наши феномены, если только признаем основные требования к шкалам и к единицам изме­рения. Многие меры, особенно в области ощущений и восприятий, являются психофизическими, так как они определяются характеристиками стимула. Дру­гие меры, в которых такие свойства стимулов менее очевидны, являются просто психометрическими, со­держащими только отношения между психически­ми феноменами. Во всех случаях шкала измерений будет более полезной, если это шкала отношений, а не шкала порядка, интервалов или номинальная.

Т.Энген

ОСНОВНЫЕ МЕТОДЫ ПСИХОФИЗИКИ *

Сам Фехнер предложил три психофизических метода, которые вошли в психологию под именем основных методов. В литературе описываются и мно­гие другие методы, но обычно они являются моди­фикациями одного из этих трех методов. Эти основ­ные методы сходны в одних отношениях и весьма различны в других. Все эти методы могут быть ис­пользованы для определения понятий, о которых шла речь выше. Выбор того или иного метода чаще всего зависит от двух практических и технических сообра­жений: 1) характер континуума стимулов, т.е. могут ли стимулы изменяться непрерывно (или по край­ней мере очень малыми шагами) или же они могут быть предъявлены только в дискретном виде. Исполь­зование дискретного предъявления стимулов необ­ходимо, например, при изучении вкуса и обоняния; 2) характер организации стимуляции, например, од­новременное или последовательное предъявление пар стимулов. В этом смысле при исследовании зрения мы располагаем большей свободой, чем при иссле­довании слуха. Сначала очень коротко, а затем более подробно рассмотрим основные психофизические методы.

1. Метод границ(едва заметных различий, ми­
нимальных изменений или серийного исследования).
Это самый прямой метод определения порога. При
определении разностного порога экспериментатор
изменяет сравниваемый стимул малыми шагами в
восходящих и нисходящих рядах. Испытуемый при
каждом изменении стимула должен сказать меньше,
равен или больше переменный стимул по сравне­
нию со стандартным. В результате эксперимента оп­
ределяются значения переменного стимула, соответ­
ствующие смене категории ответа. При определении
абсолютного порога стандартный стимул не предъяв­
ляется и задача испытуемого состоит в том, чтобы
отвечать, обнаруживает он стимул или нет.

2. Метод установки(средней ошибки, воспро­
изведения или метод подравнивания). При опреде­
лении разностного порога испытуемый, как прави­
ло, сам подстраивает сравниваемый стимул, кото­
рый может непрерывно изменяться, к стандарту, т.е.
устанавливает такое значение переменного стиму­
ла, при котором он кажется равным стандарту. Эта
процедура повторяется несколько раз, а затем вы­
числяется среднее значение и вариабельность уста­
новок испытуемого. Среднее значений подравнива­
ний (установок) является прямым показателем точ­
ки субъективного равенства, а вариабельность под­
равниваний, допускаемая испытуемым, может быть
использована для вычисления разностного порога.
При определении абсолютного порога испытуемый
неоднократно устанавливает такое значение перемен­
ного стимула, которое по его мнению является са­
мым низким среди обнаруживаемых им стимулов.

* Проблемы и методы психофизики / Под ред. А.Г.Асмолова, М.Б.Михалевской. М.: Изд-во Моск. ун-та, 1974. С. 107-116, 119— 130.

Среднее этих установок принимается за абсолютный порог.

3. Метод постоянных раздражителей(метод ис­тинных и ложных случаев или метод частот). В этом методе используется несколько постоянных дискрет­ных значений сравниваемого стимула. При опреде­лении разностного порога каждое из них сравнива­ется со стандартным стимулом много раз. Для каж­дого из значений сравниваемого стимула подсчиты-вается относительная частота разных ответов, напри­мер, ответов "меньше" и "больше". Если в опыте ис­пользуются только две категории ответов, то испы­туемый будет давать правильный ответ в половине случаев даже при одном только угадывании. Поэто­му его разностный порог определяется как прира­щение или уменьшение величины сравниваемого стимула относительно стандартного, правильно оце­ниваемое им в 75% проб, т.е. посредине между 50% (случайная удача) и 100%. Это значение, соответ­ствующее 75%, определяется интерполяцией или каким-либо другим из нескольких возможных ста­тистических методов. Когда добавляется третья кате­гория ответов типа "равно", "сомнительно" и тому подобное, метод постоянных раздражителей стано­вится очень похож на метод границ. Метод постоян­ных раздражителей может быть использован также для измерения абсолютного порога. В этом случае стандартный раздражитель не применяется, а за аб­солютный порог принимают такое значение срав­ниваемого стимула, который вызывает равное чис­ло ответов "да" и "нет".

Метод границ Абсолютный порог

Процедура опыта и вычисления при определе­нии нижнего порога высоты звука методом границ показаны в табл. 1 (взята у Титченера). Испытуемый получает инструкцию отвечать "да", когда он слы­шит тон, и "нет", когда он его не слышит в течение определенного интервала времени, указываемого эк­спериментатором. Перед основным опытом следует провести несколько предварительных тренировочных проб, чтобы убедиться, что испытуемый усвоил про­цедуру опыта. Словесные инструкции трудно сделать краткими и ясными и часто они дают худшие ре­зультаты, чем предварительная тренировка.

В первом столбце (читать сверху вниз) указаны ответы испытуемого на стимулы, предъявляемые в нисходящем ряду. Экспериментатор начинает этот ряд со сравниваемого стимула, равного 24 Гц и испытуе­мый отвечает "да". В каждой следующей пробе экспе­риментатор уменьшает частоту переменного стиму­ла на 1 Гц, испытуемый продолжает давать положи­тельный ответ до тех пор, пока частота переменного стимула не становится равна 14 Гц; тогда испытуемый отвечает "нет". Итак, порог лежит между 14 и 15 Гц. За порог принимается средняя точка — 14,5 Гц и эта величина L записывается под первым столбцом как одно из значений абсолютного порога. Затем экспе­риментатор предъявляет стимулы в восходящем ряду, начиная с 10 Гц, т.е. значительно ниже только что измеренного порога и получает ответ "нет". Экспе-

Таблица 1

Определение	порога раздражения методом границ: нижний предел восприятия высоть	звука
Частота			Чередующиеся	восходящие и нисходящие ряды
(Гц)	А	т	А	т	А	Т	А	т	А	А
	Да
	Да
	Да		Да
	Да		Да
	Да		Да						Да
	Да		Да				Да		Да
	Да	Да	Да		Да		Да		Да
	Да		Да		Да		Да		Да
	Да	Да	Да		Да		Да		Да
	Да	Нет	Да	Да	Да	Да	Да		Да	Да
	Нет	Нет	Нет	Нет	?•	Нет		Да		Нет
		Нет		Нет		Нет		Нет		Нет
		Нет		Нет		Нет		Нет		Нет
		Нет		Нет		Нет		Нет
		Нет		Нет				Нет
				Нет				Нет
				Нет				Нет
				Нет				Нет
1) L=	14,5	15,5	14,5	14,5	14,5	14,5	14,5	13,5	14,6	14,5
М = 14,5
а = 0,45
2) Уср. L	15,0		,5		14,5		14,0		14,5
М = 14,5
сг = О,32

риментатор увеличивает частоту переменного сти­мула снова на 1 Гц в каждой пробе и получает поло­жительный ответ при частоте 16 Гц. Таким образом, L = 15,5 Гц. Чередующиеся нисходящие и восходя­щие ряды повторяются возможно большее число раз или до тех пор, пока экспериментатор не убедится в относительном единообразии величины L. В после­дующих рядах он изменяет начальную точку, чтобы у испытуемого не формировались ложные представ­ления. Трудно оценить околопороговые стимулы и даже добросовестный испытуемый может впасть в ошибку, руководствуясь каким-нибудь побочным признаком, который по его мнению облегчает вы­полнение задания.

Вычисление абсолютного порога по этим дан­ным проводится следующим образом: величины RL могут быть усреднены (среднее арифметическое) тремя способами (два из них указаны внизу табли­цы: 1) все отдельные величины L, указанные под верхней линией, суммируются и усредняются. Сред­нее значение — 14,5 Гц принимается за абсолютный порог. Среднее квадратичное отклонение этого рас­пределения отражает вариабельность работы наблю­дателя; 2) под второй линией п