Расчет ЦЕНТРАЛЬНО-сжатых элементов постоянного цельного сечения
Общие сведения о работе
На сжатие работают стойки, подкосы, верхние пояса и отдельные стержни ферм и других сквозных конструкций. В сечениях сжатого элемента от сжимающего усилия N, действующего вдоль его оси, возникают почти одинаковые по величине нормальные сжимающие напряжения. Длина сжатых элементов конструкций, как правило, существенно превышает размеры поперечного сечения, и элементы разрушаются в результате потери устойчивости, которая происходит раньше, чем напряжения сжатия достигнут предела прочности. При потере устойчивости сжатый элемент теряет несущую способность и выгибается в сторону. Относительно короткие, редко применяемые элементы, разрушаются только от сжатия без потери устойчивости.
Прочность стержня при сжатии и потеря устойчивости зависят от площади A и формы его сечения, длины и типа закрепления его концов, что учитывается коэффициентом устойчивости φ, называемым иногда коэффициентом продольного изгиба.
Сжатые деревянные элементы рассчитывают по прочности и устойчивости при действии продольных сил сжатия N от расчетных нагрузок.
 Рис. 2.1. Сжатый элемент Рис. 2.1. Сжатый элемент |
Расчетные формулы
Расчет центрально-сжатых цельных элементов постоянного сечения следует производить по формулам:
а) на прочность
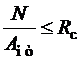 ;(2.1)
;(2.1)
б) на устойчивость
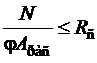 ,(2.2)
,(2.2)
где Rс- расчетное сопротивление древесины сжатию вдоль волокон; φ - коэффициент продольного изгиба; AНТ - площадь нетто поперечного сечения элемента; Aрасч - расчетная площадь поперечного сечения элемента, принимаемая равной:
Aрасч = Aбр - при отсутствии ослабления или если ослабления в опасных сечениях не выходят на кромки и их площадь не превышает 25 % Aбр, где Aбр, -площадь сечения брутто;
Aрасч = (4/3) Aбр - если ослабления не выходят на кромки и их площадь превышает 25 % Aбр;
Aрасч = Aнт-при симметричных ослаблениях, выходящих на кромки.
Опасными зонами для центрально-сжатых элементов считаются следующие участки:
для элементов с шарнирным закреплением концов - средний участок, равный половине длины элемента;
для элементов с одним шарнирно-закрепленным и другим защемленным концом - вся длина элемента;
для элементов с одним защемленным и другим свободным нагруженным концом - участок, привыкающий к защемлению, равный половине длины элемента.
Коэффициент продольного изгиба φ следует определять по формулам: при гибкости элемента λ ≤70
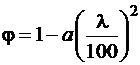 ; (2.3)
; (2.3)
при гибкости элемента λ>70
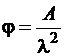 ,(2.4)
,(2.4)
где коэффициент а = 0,8 для древесины и а = 1 для фанеры, коэффициент А = 3000 для древесины и А = 2500 для фанеры.
Гибкость элементов цельного сечения определяют по формуле 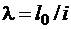 , где
, где 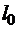 - расчетная длина элемента; i - радиус инерции сечения элемента с максимальными размерами брутто соответственно относительно осей x или y.
- расчетная длина элемента; i - радиус инерции сечения элемента с максимальными размерами брутто соответственно относительно осей x или y.
Расчетную длину элементов 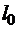 следует определять умножением его свободной длины l на коэффициент μ0:
следует определять умножением его свободной длины l на коэффициент μ0: 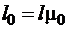 .
.
Расчетная длина учитывает влияние типа закрепления концов на устойчивость сжатого элемента. При обоих шарнирно закрепленных концах она равна геометрической длине 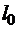 = l. При нижнем заделанном, а верхнем свободном конце -
= l. При нижнем заделанном, а верхнем свободном конце - 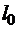 = 2,2 l. При нижнем заделанном, а верхнем шарнирном конце -
= 2,2 l. При нижнем заделанном, а верхнем шарнирном конце - 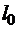 = 0,8 l, при обоих заделанных концах -
= 0,8 l, при обоих заделанных концах - 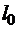 = 0,65 l.
= 0,65 l.
Радиус инерции сечения i зависит от площади A и момента инерции сечения I, т. е. 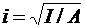 . Радиусы инерции прямоугольных сечений с размерами b и h (где h - меньший размер сечения) и круглых сечений диаметром d можно принимать равными 0,289h и 0,25d.
. Радиусы инерции прямоугольных сечений с размерами b и h (где h - меньший размер сечения) и круглых сечений диаметром d можно принимать равными 0,289h и 0,25d.
Гибкость сжатых элементов ограничивается предельной гибкостью λпр с тем, чтобы они не получились недостаточно надежными λ ≤ λпр. Основные элементы конструкций - отдельные стойки, пояса и опорные раскосы ферм и др. - должны иметь гибкость не более 120, прочие сжатые элементы основных несущих конструкций - не более 150 и сжатые элементы связей - не более 200.
Указания по подбору сечения
Подбор сечения центрально-сжатых элементов производят методом попыток, последовательных приближений и считают законченным, если дальнейшее уменьшение размеров поперечного сечения приводит к невыполнению условий прочности или устойчивости.
Размеры поперечного сечения прямоугольной формы следует принимать, руководствуясь сортаментом пиломатериалов по ГОСТ 24454-80Е (прил. 1). При круглых сечениях необходимо иметь в виду, что диаметр бревен в их тонком конце d должен приниматься кратным 0,02 м, а диаметр в расчетном сечении - с учетом сбега. Величина сбега равна 0,008 м на 1 м длины, а для лиственницы – 0,01 м на 1 м длины.
Центрально-сжатые элементы из брусьев следует проектировать равноустойчивыми, чтобы гибкости относительно осей x и y были равны, а это значит, что соотношение сторон поперечного сечения должно быть равным или близким соотношению длин. При выполнении этой рекомендации площадь поперечного сечения элемента будет наименьшей.
Зная расчетные длины l0x, l0y и предельную гибкость λпр, можно определить возможные наименьшие размеры поперечного сечения:
круглого - 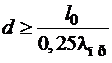 ; (2.5)
; (2.5)
прямоугольного - 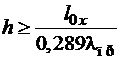 ,
, 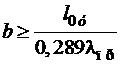 (2.6)
(2.6)
и таким образом уменьшить количество попыток при подборе сечения.
Можно предварительно приближенно задаться величинами λ и φ. Например: для основных стоек следует принимать гибкость λ = 80 и φ = 0,5; для не основных элементов гибкость - λ = 120 и φ = 0,2; для элементов связей - λ = 180 и φ = 0,1. Требуемую площадь сечения Aтр можно определить по формуле 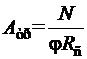 и затем подобрать размеры сечения. Гибкость отдельных элементов прямоугольного сечения следует определять в направлении обеих осей сечения и принимать для расчета наибольшую.
и затем подобрать размеры сечения. Гибкость отдельных элементов прямоугольного сечения следует определять в направлении обеих осей сечения и принимать для расчета наибольшую.
Относительно короткие элементы, длина которых не превышает семикратной высоты сечения, работают на сжатие без потери устойчивости. Расчет таких элементов проводят только на сжатие.
Задание
Подобрать сечение центрально-сжатого элемента и проверить его на прочность и устойчивость. Исходные данные взять по варианту задания из табл. 2.1, 2.2 и рис. 2.2, 2.3.
Пример расчета
Исходные данные
Расчетная сжимающая сила N = 65 кН= 0,065 МН Свободная длина l = 3,3м. Древесина сосны 2 сорта.
Условия эксплуатации конструкции: класс ответственности здания II; температурно-влажностный режим здания А3; установившаяся температура воздуха 40оС; отношение постоянных и длительных нагрузок к полной равно 0,8.
Решение
1. Определяем расчетные длины:
относительно оси x - l0x = l0 μ0x = 3,3·2,2 = 7,26м, как длястержнясодним защемленным и другим свободным нагруженным концом;
относительно оси y - l0y = l0μ0y= 3,3·1,0 = 3,3 м, как длястержня с шарнирно-закрепленными концами.
2. Определяем наименьшие возможные размеры поперечного сечения по предельному значению гибкости:
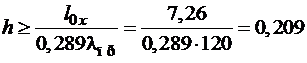 м;
м; 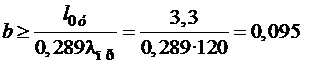 м.
м.
Принимаем ширину сечения b в соответствии с сортаментом 0,10 м.
Из условия равноустойчивости 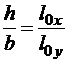 , высоту сечения следует принять
, высоту сечения следует принять 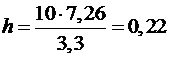 м.
м.
Принимаем ближайший больший по сортаменту размер 0,225 м.
Определяем гибкости:

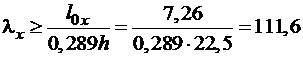 ;
; 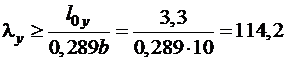 .
.
3. По большей гибкости определяем коэффициент продольного изгиба. Так как λmax = 114,2 > 70, то φ определяем по формуле (2.4)
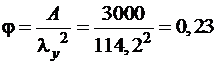 .
.
4. Для сосны 2-го сорта при ширине сечения b = 0,10 м табличное значение расчетного сопротивления сжатию равно: Rст = 13 МПа. Определяем значение расчетного сопротивления с учетом коэффициентов условий работы (п. 3.2 [1]) и коэффициента надежности по ответственности (прил. 2) по формуле (1.4):
Rс= Rстmтmвmдmn / γn = 13·0,9·0,9·1·1 / 0,95 = 11,49МПа.
Расчетная площадь поперечного сечения
Aрас = Aбр = 0,10·0,225 = 0,0225 м2, так как ослабление расположено вне зоны опасных сечений.
5. Проверяем элемент на устойчивость по формуле (2.2):
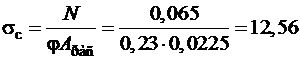 МПа.
МПа.
Так как σc > Rс = 11,49 МПа, условие устойчивости не выполняется. Необходимо увеличить размеры сечения.
Увеличиваем высоту сечения до 0,25 м. Ширина осталась без изменения и, соответственно, не изменилась гибкость.
Тогда при Aрасч = 0,10·0,25 = 0,025 м2,
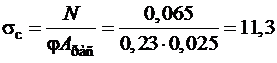 < Rс = 11,49 МПа.
< Rс = 11,49 МПа.
6. Проверяем ослабленное сечение с с площадью
Aнт = 0,25(0,10 − 2·0,02) =0,015 м2на прочность по формуле (2.2):
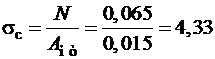 МПа < Rс=11,49 МПа.
МПа < Rс=11,49 МПа.
Так как условия прочности и устойчивости выполнены, окончательно принимаем сечение элемента 0,10х0,25 м.
2.6. Исходные данные к заданию по подбору сечения
центрально-сжатого элемента
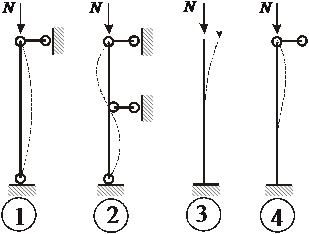
Рис. 2.2. Схемы закрепления концов стержней
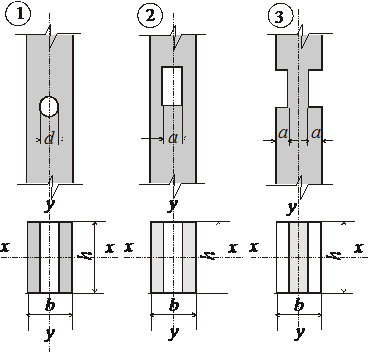
Рис. 2.3. Схемы ослабления сечений
Таблица 2.1
| Номер задания | Расчетная сила сжатия, кН | Длина стержня, м | Номер схемы закрепления концов стержня относительно осей | Вид материала | Ослабление сечения | Предельная гибкость | ||||
| Номер схемы | Размер, м | Место* | ||||||||
| x - x | y – y | |||||||||
| 85,0 | 6,0 | Брус | 0,03 | Б | ||||||
| 135,0 | 3,2 | Бревно | 0,02 | А | ||||||
| 52,5 | 3,4 | Брус | 0,018 | А | ||||||
| 40,0 | 4,8 | Брус | 0,03 | Б | ||||||
| 220,0 | 5,0 | Бревно | 0,04 | А | ||||||
| 92,0 | 3,7 | Брус | 0,018 | А | ||||||
| 73,0 | 3,8 | Брус | - | - | - | |||||
| 331,0 | 3,5 | Бревно | - | - | - | |||||
| 289,0 | 4,5 | Брус | 0,05 | Б | ||||||
| 147,5 | 5,5 | Брус | 0,02 | А | ||||||
| 310,0 | 6,5 | Бревно | - | - | - | |||||
| 140,0 | 3,6 | Брус | 0,016 | А | ||||||
| 12,5 | 5,5 | Брус | 0,03 | А | ||||||
| 230,0 | 6,0 | Бревно | 0,03 | Б | ||||||
| 141,0 | 4,2 | Брус | - | - | - | |||||
| 50,0 | 3,2 | Брус | 0,02 | А | ||||||
| 312,0 | 4,6 | Бревно | 0,05 | Б | ||||||
| 224,0 | 3,7 | Брус | 0,02 | Б | ||||||
| 150,0 | 6,2 | Брус | 0,018 | А | ||||||
| 268,0 | 5,8 | Бревно | - | - | - | |||||
| 37,0 | 3,5 | Брус | 0,02 | Б | ||||||
| 240,0 | 4,0 | Бревно | - | - | - | |||||
| 88,0 | 5,4 | Бревно | 0,03 | А | ||||||
| 222,0 | 6,1 | Брус | 0,04 | Б | ||||||
| 238,0 | 4,0 | Брус | 0,05 | А |
* А – ослабление в пределах опасной зоны, Б – вне опасной зоны.
Таблица 2.2
| Номер задания | Класс ответственности здания | Температурно-влажностные условия эксплуатации | Установившаяся температура воздуха, (ºС) | Отношение постоянных и длительных временных нагрузок к полной | Порода | Сорт |
| II | Б2 | <35 | <0,8 | Лиственница | ||
| III | А1 | >0,8 | Сосна | |||
| II | А3 | <35 | <0,8 | Пихта | ||
| I | Б1 | <35 | <0,8 | Береза | ||
| III | Б2 | <35 | >0,8 | Осина | ||
| III | А3 | <0,8 | Кедр | |||
| II | А3 | <35 | >0,8 | Ель | ||
| I | В3 | <35 | >0,8 | Лиственница | ||
| II | Б3 | <35 | <0,8 | Сосна | ||
| II | А3 | <35 | >0,8 | Пихта | ||
| III | А2 | <0,8 | Береза | |||
| III | В2 | <35 | <0,8 | Осина | ||
| II | В1 | <35 | >0,8 | Кедр | ||
| II | Г1 | <35 | >0,8 | Ель | ||
| I | А2 | <0,8 | Лиственница | |||
| I | Б3 | <35 | <0,8 | Сосна | ||
| II | В1 | <35 | >0,8 | Пихта | ||
| III | А1 | <35 | >0,8 | Береза | ||
| II | В2 | >0,8 | Осина | |||
| I | Б3 | <0,8 | Кедр | |||
| II | А2 | <35 | <0,8 | Ель | ||
| III | В2 | <35 | <0,8 | Сосна | ||
| II | Г2 | <35 | >0,8 | Пихта | ||
| I | Б3 | <0,8 | Береза | |||
| II | А1 | >0,8 | Осина |
Расчет на поперечный изгиб
Общие сведения
Изгибаемые элементы - балки, прогоны, доски настилов и обшивок - наиболее распространенные элементы деревянных конструкций. В изгибаемом элементе от нагрузок, действующих поперек его продольной оси, возникают изгибающие моменты М и поперечные силы Q, определяемые методами строительной механики.
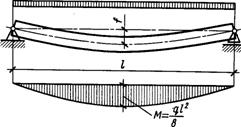 Рис. 3.1. Схема изгибаемого элемента Рис. 3.1. Схема изгибаемого элемента |
От действия изгибающего момента в сечениях элемента возникают напряжения изгиба, которые состоят из сжатия в верхней половине сечения и растяжения в нижней. В результате элемент изгибается.
Изгибаемые элементы работают еще более надежно, чем сжатые, и предупреждают об опасности разрушения заранее большими прогибами.
Изгибаемые элементы, как и сжатые, рекомендуется изготовлять из древесины 2-го сорта. В малоответственных элементах можно применять древесину 3-го сорта.
Изгибаемые элементы рассчитываются по первой и второй группе предельных состояний.
Расчетные формулы
3.1.1. Расчет по первой группе предельных состояний
1. Расчет изгибаемых элементов, обеспеченных от потери устойчивости плоской формы деформирования, на прочность по нормальным напряжениям следует производить по формуле
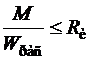 , (3.1)
, (3.1)
где М - расчетный изгибающий момент; Rи - расчетное сопротивление изгибу; Wрас - расчетный момент сопротивления поперечного сечения элемента.
Для цельных элементов Wрас = Wнт. При наличии ослаблений в пределах длины равной 0,20 м в разных сечениях, при определении Wнт все ослабления на этой длине суммируются.
