Анализ простых ассерторических суждений в простой традиционной силлогистике

3.1. Специфика анализа простых ассерторических суждений в простой традиционной силлогистике

Простая традиционная силлогистика, восходящая к силлогистике Аристотеля и составляющая главный компонент традиционной логики, пошла по пути выявления упрощенной логической формы простого суждения, а именно: все простые суждения в ней рассматриваются как атрибутивные. Это стало возможным потому, что любое реляционное суждение, состоящее из двух и более субъектов, т. е. суждения вида

R(a,b), R(a₁,a₂,…,a_n), можно, не изменяя содержания, переформулировать и свести к суждению с более простой логической формой, которую имеет атрибутивное суждение. Более простая логическая форма атрибутивного суждения особенно очевидна в случае единичных атрибутивных суждений: в них в традиционной логике выделяют ровно один субъект, один предикат и одну связку.

Пример. Москва есть столица России.

Под субъектом атрибутивного суждения в традиционной логике понимают то, о чем в нем нечто утверждается либо отрицается. Субъект суждения обозначается латинской буквой S (первая буква латинского слова «Subjectum» – подлежащее, субъект; см. Словарь И.Х. Дворецкого); под предикатом – сам признак, наличие или отсутствие которого утверждается в суждении. Предикат суждения обозначается буквой P (первая буква латинского слова «Praedicatum» – сказуемое). Связка в русском языке передаётся словом «есть» и выражает логическую связь между S и P атрибутивного суждения. В случае единичного атрибутивного суждения она выражает отношение (не) принадлежности элемента S классу предметов, мыслимых в P.

Таким образом, логическая форма единичного утвердительного атрибутивного суждения будет иметь вид S есть P, а единичного отрицательного атрибутивного суждения – S не есть P.

3.2. Канонический и неканоческий вид единичных простых суждений

Для точного логического анализа умозаключений следует различать канонический и неканонический вид суждения. Если в суждении в явном виде представлены субъект, предикат и связка, то такое суждение имеет канонический вид. Например, единичное суждение «Иванов есть студент» является суждением канонического вида, а суждение «Иванов сдал зачёт по логике» имеет неканонический вид, так как в нём в явном виде представлен только субъект под именем «Иванов». Такая ситуация является характерной для естественного языка, в котором выражаются суждения в виде повествовательных предложений. Как известно, естественные языки не имеют точных синтаксических (правил построения сложных выражений языка из простых) и семантических (правил приписывания смысла и значения выражениям языка) правил, что позволяет пользователю языка в процессах речевой практики кратчайшим способом выражать свои мысли. Однако ценой этого достоинства естественного языка является то, что он строго не следует за логической формой мысли, которую он выражает. В частности, грамматическая форма повествовательных предложений как определённых языковых единиц строго не следует за логической формой суждений, которые они выражают, т.е. повествовательные предложения очень часто репрезентируют в себе суждения в неканоническом виде, что чревато возможностью логических ошибок в рассуждении. Во избежание ошибок в рассуждении необходимо посредством переформулировки повествовательного предложения приводить суждения неканонического вида к суждению канонического вида по схеме «S (не) есть P». Так, в случае суждения неканонического вида «Иванов сдал зачёт по логике» в результате переформулировки предложения, которое его выражает, мы получим следующее суждение канонического вида: «Иванов есть студент, который сдал зачёт по логике», где S – Иванов, P – студент, который сдал зачет по логике, а связка представлена словом «есть».

3.3. Объединённая классификация атрибутивных суждений по количеству и качеству

Для одновременного учёта всех важных логических свойств суждений в традиционной логике используется объединённая классификация атрибутивных суждений по количеству и качеству. В этой классификации выделяются четыре типа (вида) суждений: суждения вида (типа) A, E, I, O.

I. Суждения вида (типа) A. К ним относятся:

1) Общеутвердительные суждения с логической формой «Все S есть P».

Например, «Все города (S) есть населённые пункты (P)».

2) Единично - утвердительные суждения с логической формой «S есть P».

Например, «Калининград (S) есть населённый пункт (P)».

II. Суждения вида (типа) E. К ним относятся:

1) Общеотрицательные суждения с логической формой «Все S не есть P» («Ни один S не есть P»).

Например, «Все герои (S) не есть трусы (P)», либо «Ни один герой (S) не есть трус (P)». Интуитивно ясно, что данные суждения логически равнозначны.

2) Единично-отрицательные суждения с логической формой «S не есть P».

Например, «А. С. Пушкин не есть космонавт».

III. Суждения вида (типа) I.

I. Частноутвердительные суждения с логической формой «Некоторые S есть P».

Например, «Некоторые студенты есть спортсмены».

IV. Суждения вида (типа) O.

Частноотрицательные суждения с логической формой
«Некоторые S не есть P».

Например, «Некоторые студенты не есть спортсмены».

В данной классификации выбор латинских букв A, E, I, O в качестве названий видов (типов) суждений опирается на следующие мнемонические соображения.

Латинский термин «affirmo» в переводе на русский язык означает утверждаю. Поскольку суждения, выделенные в рубриках I и III, являются утвердительными, т. е. имеют одно и то же качество и различаются только по количеству, то первая гласная термина «affirmo», т.е. a(А), взята для названия общеутвердительных и единично - утвердительных суждений, а вторая гласная термина «affirmo», т.е. i(I), взята для названия частноутвердительных суждений.

Соответственно латинский термин «nego» в переводе на русский язык означает отрицаю. Поэтому первая гласная этого термина, т. е. е(E) взята для названия общеотрицательных и единично - отрицательных суждений, а вторая гласная этого термина, т.е. о(O), взята для названия частноотрицательных суждений.

В современных учебниках по общей логике используется более краткая запись логических форм суждений A, E, I, O.

Так, в А вместо выражений логических форм «Все S есть P» и «S есть P» употребляется их краткая запись в виде «S а P», где «а» есть сокращение словосочетания «Все … есть …» либо «… есть …»; в E вместо выражений «Все S не есть P», «Ни один S не есть P», либо «S не есть P» употребляется выражение «S е P», где «e» есть сокращение «словосочетаний «Все … не есть …», «Ни один … не есть …» либо «… не есть …»; в I вместо «Некоторые S есть P» пишется «S i P», где «i» есть сокращение выражения «Некоторые … есть …»; в O вместо «Некоторые S не есть P» пишется «S о P», где «о» есть сокращение выражения «Некоторые … не есть …»

Логические термины «все» и «ни один», входящие в записи логических форм некоторых суждений вида (типа) A, E, а также логический термин «некоторые», входящий в запись логических форм суждений I, O, называются кванторными словами. Кванторные слова (от латинского quantum – сколько) есть слова, которые указывают на характеристику суждений по количеству.

3.4. Категорические суждения вида (типа) A, E, I, O, их канонический и неканонический вид

В объединённой классификации суждений по количеству и качеству речь идёт не просто об атрибутивных, а об атрибутивных категорических суждениях A, E, I, O.

При этом под категорическими суждениями в традиционной логике следует понимать суждения A, E, I, O, в которых выполнены следующие два условия.

I. Первое условие. Кванторным словам приписан точный смысл: кванторное слово «все» следует понимать не в собирательном, а в разделительном смысле, т.е. в смысле «каждый»; а кванторное слово «некоторые» следует понимать не только в смысле «не все», а в более широком смысле, т.е. в смысле «хотя бы один (а может быть, и все)».

Примеры. Суждение вида А: «Все студенты есть учащиеся» нужно понимать как «Каждый студент есть учащийся». Соответственно суждение вида I «Некоторые студенты есть спортсмены» следует понимать как «Хотя бы один студент есть спортсмен», или, говоря по-другому, «Существует студент, который является спортсменом».

Два последних примера модификации суждения I показывают, что выражения «хотя бы один» и «существует» являются логическими синонимами. При этом как выражение «хотя бы один», так и выражение «существует» предполагают, что суждения вида I: «Некоторые S есть P» и суждения вида О: «Некоторые S не есть P» будут истинными в следующих случаях:

1) когда один предмет из множества S (не) обладает свойством P;

2) когда более чем один, но не все предметы из S (не) обладают

свойством P;

3) когда каждый предмет из S (не) обладает свойством P.

Например, суждение «Некоторые студенты нашей группы посетили

Варшаву» будет истинным в случаях:

1) Если всего лишь один студент из нашей группы посетил Варшаву;

2) если два, три … и т. д., но не все студенты из нашей группы посетили Варшаву;

3) наконец, если каждый студент нашей группы побывал в Варшаве.

II. Второе условие. Даны точные определения утвердительного и отрицательного суждения.

Суждение X является отрицательным, если в нём есть отрицание и отрицание стоит либо в начале суждения, либо непосредственно перед связкой. В противных случаях суждение X является утвердительным.

Примеры отрицательных суждений.

1) Неверно, что Варшава есть столица Франции.

2) Варшава не есть столица Франции.

Примеры утвердительных суждений.

1) Эта книга есть источник больших знаний.

2) Эта книга есть художественное произведение, которое не пользуется широкой популярностью.

Следует иметь в виду, что в обычной разговорной практике суждения A, E, I, O фигурируют чаще всего в неканоническом виде, т.е. в них могут быть нечётко выделены либо опущены (но подразумеваются) или кванторные слова, или субъект, или связка, или предикат.

Примеры.

1. Кража есть аморальный поступок. Это суждение есть суждение вида А, которое имеет неканонический вид, так как в нем опущено, но подразумевается кванторное слово «все». Его канонический вид: Все кражи есть аморальные поступки.

2. Иногда граждане России нарушают Уголовный кодекс.

Это суждение есть суждение вида I, которое имеет неканонический вид, так в нём слово «иногда» замещает кванторное слово «некоторые»; опущена (но подразумевается) связка «есть», нечетко выделен предикат. Его канонический вид: Некоторые граждане России есть люди, которые нарушают Уголовный кодекс.

Описанные ситуации показывают, что суждения A, E, I, O правомерно называть категорическими лишь после того, когда они приведены к каноническому виду.

3.5. Отношения между суждениями A, E, I, O. Логический квадрат

В современной логике содержание мысли принято называть интенсионалом, а её предметное значение – экстенсионалом. В этих терминах содержание понятия есть его интенсионал; а его объём – экстенсионал.

Аналогично в учении о суждении как форме мышления содержание суждения есть его интенсионал, а его истинностное значение есть его экстенсионал.

В главе 2 Понятие как форма мышления мы рассмотрели вопрос об отношении между понятиями по содержанию (интенсионалу) и объёму (экстенсионалу).

Аналогично в главе 3 Суждение как форма мышления. Простые суждения мы рассмотрим вопрос об отношении между простыми суждениями A, E, I, O по содержанию (интенсионалу) и истинностным значениям (экстенсионалу).

По содержанию суждения A, E, I, O могут находится друг с другом в отношении сравнимости либо несравнимости.

Суждение X (из A, E, I, O) сравнимо по содержанию с суждением Y (из A, E, I, O), если и только если понятия, стоящие в них на местах S и P, совпадают с точностью до перестановки. В противных случаях суждение X несравнимо по содержанию с суждением Y.

Примеры сравнимых по содержанию суждений.

1) X: Все липы (S) есть деревья (P).

Y: Некоторые липы (S) не есть деревья (P).

2) X: Все города(S) есть населенные пункты(P).

Y: Некоторые населённые пункты(P) есть города(S).

Примеры несравнимых по содержанию суждений.

1) X: Все студенты(S) есть учащиеся(P).

Y: Все футболисты(S) есть спортсмены(P).

В этих суждениях, как нетрудно видеть, не совпадают S (субъекты) и не совпадают P (предикаты).

2) X: Все берёзы(S) есть деревья(P).

Y: Все сосны(S) есть деревья(P).

В этих суждениях, как нетрудно видеть, совпадают Р, но не совпадают S.

3) X: Все футболисты(S) есть спортсмены(P).

Y: Все футболисты(S) есть люди(P).

В этих суждениях совпадают S, но не совпадают P.

Для дальнейшего анализа рассуждений на предмет их логичности либо нелогичности важно выяснить отношения между сравнимыми множественными суждениями по их истинностным значениям.

По истинностным значениям сравнимые множественные суждения A, E, I, O могут находиться в отношении совместимости либо несовместимости.

Суждение X (из A, E, I, O) совместимо с суждением Y (из A, E, I, O), е. и т. е. они вместе истинны. В противном случае суждение X несовместимо с суждением Y. Наглядно эти определения можно выразить следующей таблицей:

Х	Y	Суждения
И	И	Отношения совместимости
И	Л	Отношения несовместимости
Л	И
Л	Л

Для наглядного, ясного и более конкретного представления отношений совместимости и несовместимости между множественными суждениями A, E, I, O в традиционной логике используют логический квадрат (ЛК). ЛК – это наглядный геометрический способ изображения конкретных отношений между суждениями A, E, I, O.

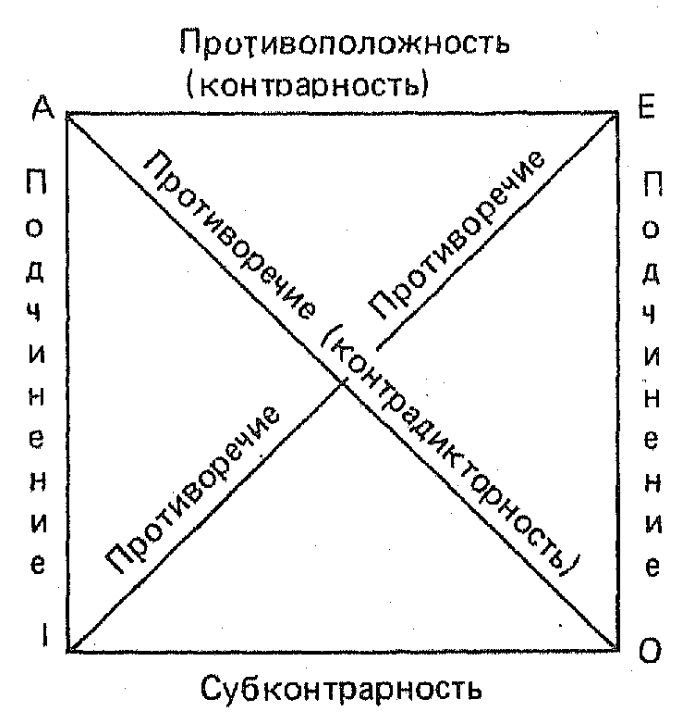
Предполагается, что в ЛК суждения A, E, I, O имеют на местах S и P одни и те же понятия. Эти суждения отличаются друг от друга только количеством и качеством. Это позволяет при содержательном формулировании одного из четырёх суждений вида A, E, I, O содержательно сформулировать оставшиеся три суждения. Например, при A: Все липы есть деревья получаем E: Ни одна липа не есть дерево; O: Некоторые липы не есть деревья – I: Некоторые липы есть деревья. Понятно, что все эти суждения сравнимы по содержанию.

Теперь опишем более конкретно отношение подчинения, отношение субконтрарности, отношение контрарности и отношение контрадикторности.

1. Отношение подчинения. Суждения, находящиеся в отношении подчинения, т. е. A, I; E, O, где A и E являются подчиняющими суждениями, а I и O – подчинёнными суждениями, характеризуются тем, что в них из истинности подчиняющих суждений с необходимостью следует истинность подчинённых суждений. Например, из истинности A: «Все кражи – аморальны» с необходимостью следует истинность суждения I: «Некоторые кражи – аморальны»; также из истинности E: «Ни один герой не есть трус» с необходимостью следует истинность суждения O: «Некоторые герои не есть трусы».

Описанная ситуация показывает, что суждения A, I, а также E, O могут быть вместе истинными, и, следовательно, они находится в отношении совместимости.

2. Отношение субконтрарности. Суждения, находящиеся в отношении субконтрарности, т.е. I, O, не могут быть вместе ложными, но могут быть вместе истинными.

Так, суждение I: «Некоторые треугольники есть квадраты» является ложным, а суждение О: «Некоторые треугольники не являются квадратами» в соответствии со смыслом кванторного слова «некоторые» является истинным. Этот пример демонстрирует случай, когда суждение I и суждение O не могут быть вместе ложными.

Соответственно суждение I: «Некоторые студенты знают логику» и суждение O: «Некоторые студенты не знают логику» демонстрируют случай их одновременной истинности. Таким образом, суждения, находящиеся в отношении субконтрарности, также могут представлять отношение совместимости.

3. Отношение контрарности. Суждения, находящиеся в отношении контрарности, т.е. A, E, не могут быть вместе истинными, но могут быть ложными. Например, суждение А: «Все студенты есть учащиеся» является истинным, а суждение Е: «Ни один студент не есть учащийся» является ложным, что демонстрирует случай, когда они не могут быть вместе истинными; если же в качестве А взять суждение «Все студенты знают логику», а в качестве E взять суждение «Ни один студент не знает логику», то тем самым мы продемонстрируем случай, когда A и E являются вместе ложными. Следовательно, суждения A и E репрезентируют отношение несовместимости друг с другом.

4. Отношение контрадикторности. Суждения, находящиеся в отношении контрадикторности, т. е. A, O, а также E, I, не могут быть вместе истинными и не могут быть вместе ложными: при истинности одного из них другое с необходимостью будет ложным и, наоборот, при ложности одного из них другое с необходимостью будет истинным. Например, при истинности А: «Все квадраты есть ромбы» суждение O: «Некоторые квадраты не есть ромбы» является ложным. Равнымобразом при ложности суждения I:«Некоторые треугольники есть квадраты» суждение E: «Ни один треугольник не есть квадрат» является истинным. Следовательно, отношение контрадикторности также демонстрирует отношение несовместимости.

Схема отношений между простыми атрибутивными суждениями A, E, I, O в логическом квадрате.

Отношения между суждениями в ЛК

отношение отношение

совместимости несовместимости

отношение отношение

подчинения субконтрарности

отношение отношение

противоположности контрадикторности

Знание описанных отношений позволяет рассуждающему ясно представлять возможности распределения истинностных значений в рассуждениях по логическому квадрату, что детально будет продемонстрировано нами в изложении вопроса «Непосредственные силлогизмы, правдоподобные и неправдоподобные умозаключения по логическому квадрату» ( см. §3 Главы 7).

3.6. Распределённость терминов в суждениях вида A, E, I, O

Для анализа логичности умозаключений средствами традиционной логики важную роль играет знание распределённости терминов, т.е. субъекта и предиката (S, P), в суждениях вида A, E, I, O. Это знание составляют следующие определения.

Термин является распределённым в суждении, если и только если он мыслится в нем в полном объеме. В противном случае термин в суждении не распределён. Этому определению можно придать следующий операциональный смысл: термин является распределенным в суждении, если объём понятия, которое он выражает, полностью входит (включается) в объём понятия, которое выражает другой термин, либо полностью исключается из объёма понятия этого другого термина. В противных случаях термин в суждении не распределён.

Рассмотрим, как распределены термины в суждениях A, E, I, O. Результаты нашего анализа оформим в виде некоторой таблицы. В случае фиксирования распределённости термина в суждении мы поставим в таблице напротив данного термина и соответствующего вида суждения знак «+», а в случае обнаружения его нераспределённости – знак «-».

Для заполнения таблицы проанализируем распределенность терминов (S, P) в каждом из суждений A, E, I, O на содержательных примерах.

1) Рассмотрим общеутвердительное суждение вида A: Все липы (S) есть деревья (P).

Интуитивно ясно, что понятие «липы», стоящее на месте субъекта S, в этом суждении мыслится в полном объеме, на что указывает и кванторное слово «все». Объем этого понятия полностью включается в объем понятия «деревья», стоящего на месте предиката P. Таким образом, в данном суждении термин S распределен.

По-другому обстоит дело с термином P, ведь в данном суждении мы мыслим в P лишь те деревья, которые являются липами, и не мыслим в P другие деревья, т.е. березы, дубы, сосны, осины и т.д. Следовательно, в данном суждении предикат P мыслится не в полном объеме, т.е. является нераспределенным. Это заключение следует и из применения операционального критерия (не)распределенности. Ведь интуитивно ясно, что объем понятия «деревья» полностью не входит в объем понятия «липы».

Очевидно также, что S будет распределен, а P не распределен и в случае рассмотрения единично-утвердительных суждений, которые, как мы отметили выше (см. объединенную классификацию суждений по количеству и качеству в ТЛ), относятся к виду А. Например, это интуитивно усматривается при анализе суждения: А.С. Пушкин (S) есть великий поэт (P).

Вывод о распределенности S и нераспределенности P в суждениях A убедительно демонстрируют диаграммы Эйлера для приведенных примеров.

Диаграмма Эйлера для суждения Диаграмма Эйлера для

Все липы (S) есть деревья (P). суждения А.С. Пушкин (S)

есть великий поэт (P).

S S Ы P U

P S. U

U – множество растений U – множество поэтов

P – множество деревьев P – множество великих поэтов

S – множество липS – А.С. Пушкин

2) Рассмотрим суждения вида E на примерах общеотрицательного суждения: Все герои (S) не есть трусы (P) и единично-отрицательного суждения: А.С. Пушкин (S) не есть космонавт (P).

Распределенность субъекта (S) и предиката (P) легко усматривается на диаграммах Эйлера для этих суждений через операциональный критерий исключенности объемов этих терминов относительно друг друга.

Диаграмма Эйлера для суждения Диаграмма Эйлера для суждения

Все герои не есть трусы. А.С. Пушкин не есть космонавт.

S P U

P   U S.

U – множество людей U – множество людей

S – множество героев S – А.С. Пушкин

P – множество трусов P – множество космонавтов

Равный образом легко усматривается на диаграммах Эйлера нераспределенность субъекта (S) и предиката (P) в суждениях вида I и нераспределенность субъекта (S) и распределенность предиката (P) в суждениях вида O через призму операционального критерия (не)распределенности этих терминов.

Примеры.

I: Некоторые студенты (S) есть спортсмены (P).

O: Некоторые студенты (S) не есть спортсмены (P).

Диаграмма Эйлера для суждения Диаграмма Эйлера для суждения

«Некоторые студенты есть «Некоторые студенты не есть

спортсмены» спортсмены».

P S U

P   S U

U – множество людей U – множество людей

S – множество студентов S – множество студентов

P – множество спортсменов P – множество спортсменов

В данных диаграммах заштрихованные части наглядно показывают, что S и Р в суждениях вида I мыслятся в неполном объеме, т.е. являются нераспределенными, а в суждениях вида О субъект (S) мыслится в неполном объеме, т.е. является нераспределенным, а предикат (Р) мыслится в полном объеме, т.е. является распределенным.

Проведенный анализ позволяет отразить полученные результаты в следующей таблице:

Виды суждений	S	P
A	+	-
E	+	+
I	-	-
O	-	+

Данная таблица показывает, что субъекты (S) распределены в общих суждениях и не распределены в частных суждениях, а предикаты (Р) распределены в отрицательных суждениях и не распределены в утвердительных суждениях.