Деление понятия как логическая операция. Понятие о классификации

7.1. Общая характеристика операции деления

В актах общения и исследования иногда необходимо точно знать, какие виды предметов входят в объём того или иного понятия. В математике эту информацию полезно знать при доказательстве обобщающих теорем о математических объектах методом рассуждения по случаям, в строительном деле, например, эта информация полезна при раздельном складировании строительных материалов, мыслимых в понятии «сыпучие строительные материалы», и т.д.

Для удовлетворения такого рода потребностей в общей практической логике имеется специальная операция с понятиями, которая называется делением понятия.

Деление понятия – это логическая операция, раскрывающая объём понятия посредством выделения в нём различных видовых понятий, объёмы которых и представляют различные виды предметов, входящие в объём исходного понятия.

Проведение данной операции предполагает выделение делимого понятия, основания деления и членов деления.

Делимое понятие – это понятие, объём которого раскрывается; основание деления – это признак, на основе которого образуются видовые понятия; члены деления – это сами видовые понятия, в объёме которых мыслится ровно один вид предметов из объёма исходного (делимого) понятия.

7.2. Виды деления понятия

В общей практической логике целесообразно выделить следующие виды деления понятий.

а) Деление понятия по видоизменению признака – это такое деление, в котором на основе количественного изменения основания деления последовательно выделяются различные виды предметов, входящие в объём делимого понятия.

Пример 1. Пусть делимое понятие есть понятие «треугольник»; основание деления – признак «величина угла». Тогда, количественно увеличивая основание деления, т.е. величину угла, мы в структуре понятия «треугольник» последовательно выделим видовыепонятия «остроугольный треугольник», «прямоугольный треугольник», «тупоугольный треугольник» и соответственно в их объёмах выделим качественно различные виды треугольников: остроугольные, прямоугольные и тупоугольные треугольники.

Пример 2. Пусть делимое понятие есть «естественный сыпучий строительный материал природного происхождения», основание деления – величина отдельных его видов. Тогда,мысленно количественно увеличивая основание деления – величину отдельных его видов, мы в структуре понятия «естественный сыпучий строительный материал природного происхождения» выделим последовательно видовые понятия: «глина», «песок», «гравий» и соответственно в их объёмах выделим качественно различные виды естественных сыпучих строительных материалов, т.е. глину, песок, гравий.

б) Дихотомическое деление.

Дихотомическое (от греч. διχο-τομiα – разрубание пополам, разделение надвое) – это такое деление, в котором на основе качественного варьирования некоторого основания, то есть некоторого признака, по принципу наличия либо отсутствия его у предметов, входящих в объём делимого понятия, образуются ровно два видовых понятия, находящихся друг к другу в отношении противоречия; соответственно объёмы этих видовых понятий фиксируют в себе ровно два вида различных предметов:

1) предметы, обладающие выделенным в основании признаком;

2) предметы, не обладающие выделенным в основании признаком.

Операция деления понятия может быть многоступенчатой. Однако в науке и практике дихотомическое деление часто заканчивается одним - двумя этапами, так как уже трехступенчатое дихотомическое деление становится не вполне прозрачным.

Примеры дихотомического деления в науках: в математике все числа делятся на чётные и нечетные; в физиологии все рефлексы делятся на условные и безусловные (неусловные); в политологии и социологии все противоречия делятся на антагонистические и неантагонистические; в философии все причины делятся на свободные и несвободные и т. д. В практической жизни мы всех людей делим на честных и нечестных, решительных и нерешительных, трудолюбивых и нетрудолюбивых и т. д.

Схематические представления дихотомического деления.

Пример. Пусть делимое понятие А («населённый пункт»). Тогда, используя в качестве основания деления признак – численность населения, мы можем дихотомически выделить в структуре понятия А («населенный пункт») видовое понятие В («город») и видовое понятие не-В («не-город»).

Далее, применяя определенное основание к понятию В, мы можем дихотомически выделить в его структуре видовые понятия С и не-С. Равным образом мы можем начать и продолжить методом дихотомии образование видовых понятий на базе понятия не-В. В итоге можно представить следующие схемы дихотомического деления.

Схема 1 Схема 2

А А

В не-В В не-В

С не-С Д не-Д

Дихотомическое деление эффективно применяется в следственной практике в целях сокращения числа следственных версий при раскрытии преступления.

Пример*. Пусть на окраине посёлка N Калининградской области произошло покушение на убийство. Выехавший на место преступления следователь обнаружил недалеко от стреляной гильзы охотничьего ружья клочки обгоревшей газеты, которая была использована в качестве пыжа патрона охотничьего ружья. Развернув клочок обгоревшей газеты, следователь узнал, что это часть газеты «Калининградская правда». На этом основании он разделил жителей посёлка N на жителей, которые выписывают «Калининградскую правду», и жителей, которые её не выписывают.

Далее он дихотомически разделил жителей посёлка N, которые выписывают «Калининградскую правду», также на две части: на тех, которые имеют охотничьи ружья, и тех, которые их не имеют. Жителей, которые выписывают «Калининградскую правду» и имеют охотничьи ружья, оказалось очень мало, и следственная версия легко была проверена.

в) Деление понятия на основе комбинирования двух оснований.

Практически этот вид деления применяется к понятиям, в которых обобщаются индивиды, т.е. к понятиям с логической формой xА(x). Поясним этот вид деления понятия на следующем содержательном примере.

Пусть делимое понятие есть понятие «студент». В качестве основания деления выберем:

1) наличие у студента трудолюбия

2) наличие у студента способностей к успешной учебе[24]

Далее в результате качественного варьирования данных оснований мы получим следующие словосочетания, выражающие признаки-свойства:

1) быть трудолюбивым студентом

2) быть нетрудолюбивым студентом

3) быть способным к успешной учебе

4) быть неспособным к успешной учебе

В итоге на основе делимого понятия мы можем выделить следующие видовые понятия, объёмы которых содержат все возможные качественно различные группы студентов:

1) студент, который трудолюбив и способен к учебе

2) студент, который трудолюбив, но не способен к учебе

3) студент, который нетрудолюбив, но способен к учёбе

4) студент, который нетрудолюбив и не способен к учёбе

Во избежание ошибок в рассуждениях деление понятия как логическую операцию следует отличать от мереологического деления целого на части, где целое и часть есть физические либо метафизические объекты.

Примеры логического и мереологического деления физических объектов:

Пример 1. Логическое деление: поезда делятся на грузовые и пассажирские.

Пример 2. Мереологическое деление: поезда делятся на локомотив и вагоны.

Примеры логического и мереологического деления метафизических объектов:

Пример 3. Логическое деление: университеты делятся на технические и гуманитарные.

Пример 4. Мереологическое деление: университеты делятся на факультеты и институты.

Для установления характера операции деления необходимо осуществить следующую процедуру:

из членов деления и делимого понятия построить повествовательное предложение, чтобы его подлежащим был один из членов деления, а в сказуемое вошло делимое понятие. Если при этом полученное предложение окажется истинным, то анализируемая операция является логическим делением, если – ложным, то речь идет о мереологическом делении.

Проверки примеров 1 – 4 описанным методом.

Пример 1. Грузовой поезд есть поезд (истина) – логическое деление.

Пример 2. Вагон есть поезд (ложь) – мереологическое деление.

Пример 3. Гуманитарные университеты есть университеты (истина) – логическое деление.

Пример 4. Факультет есть университет (ложь) – мереологическое деление.

7.3. Правила деления и их возможные нарушения

В общей практической логике также фиксируются четыре правила деления.

1. Правило соразмерности.

Это правило требует, чтобы объединение классов предметов, мыслимых в объёмах видовых понятий, полностью бы исчерпывало объём делимого понятия.

Формальная запись правила. Пусть А есть делимое понятие, а B₁, B₂, …, B_n есть члены деления; соответственно WA есть объём делимого понятия A, а WB₁, WB₂, …WB_n есть объёмы членов деления B₁, B₂, …, B_n. Тогда правило соразмерности будет иметь следующий вид:

WB₁ WB₂ … WB_n = WA.

При нарушении данного правила возможны следующие ошибки.

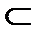1. Ошибка неполного деления. Пример. Пусть делимое понятие А есть понятие «юрист»; B₁ – «прокурор», B₂ – «судья», B₃ – «следователь». Тогда очевидно, что объединение класса прокуроров, класса судей и класса следователей не будет исчерпывать класс юристов, а будет представлять лишь правильный подкласс класса юристов, что формально выразится следующей записью: WB₁ WB₂ WB₃ WA.

Мы имеем данный результат, потому что в объединение объёмов членов деления не вошли объёмы следующих членов деления: класс адвокатов – WB₄, класс нотариусов – WB₅ и класс юрисконсультов – WB₆.

2. Ошибка обширного (с лишним членом) деления. Эта ошибка возникает, когда имеет место следующее соотношение между объединением объёмов членов деления и объёмом делимого понятия: WA 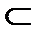WB₁ WB₂ … WB_n.

Пример. Пусть делимое понятие А – «футболист высшей лиги», B₁ –«футболист - перворазрядник», B₂ – «футболист - мастер спорта», B₃ – «футболист - заслуженный мастер спорта».

Тогда имеем: WA 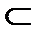WB₁ WB₂, …, WB₃, т. е. имеем формальное выражение ошибки деления с лишним членом, так как в данном случае футболисты - мастера спорта и футболисты - заслуженные мастера спорта выделены в отдельные классы, хотя логическая корректность требует рассматривать класс футболистов - заслуженных мастеров спорта в качестве правильного подкласса футболистов - мастеров спорта. Иными словами, схема соразмерного деления должна иметь следующий вид: WB₁ (класс футболистов-перворазрядников) WB₂ (класс футболистов-мастеров спорта) = WA (класс футболистов высшей лиги), где WB₂ = (класс футболистов - мастеров спорта, не имеющих звания «заслуженный» класс футболистов - мастеров спорта, имеющих звание «заслуженный»).

2. Правило исключения. Это правило требует, чтобы объёмы членов деления (видовых понятий), попарно взятые, не находились в отношении пересечения (перекрещивания). Формальное выражение данного требования: WB_i WB_j = Ø. Иными словами говоря, данное правило исключает наличие общей части в объёмах членов деления, что делает операцию деления точной и ясной процедурой.

При нарушении данного правила возникает логическая ошибка «не исключает», которая фиксирует нечёткость операции деления и вследствие этого нестрогость всего рассуждения, опирающегося на результаты ошибочного деления.

Пример ошибки «не исключает»*.

Пусть делимое понятие А – «деньги»; B₁ – «деньги, отправленные почтовым переводом»; B₂ – «деньги, не отправленные почтовым переводом»; B₃ – «утерянные деньги». Нетрудно видеть, что WB₁ WB₃ 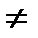Ø, так как деньги могут быть отправлены на почте почтовым переводом и не дойти до получателя вследствие непреодолимой силы, возникшей на пути их трансляции, т.е. эти деньги окажутся утерянными. Не исключён также случай: WB₂ WB₃ 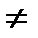Ø, так как деньги могут быть утеряны отправителем ещё по дороге на почту, и таким образом окажутся деньгами, которые не отправлены почтовым переводом.

3. Правило одного основания.Хотя деление понятия является многоступенчатой операцией и на каждом этапе деления правомерно применять разные основания деления, однако во избежание путаницы в рассуждении необходимо, чтобы при делении понятия неукоснительно выполнялось следующее требование: на каждом этапе деления члены деления должны получаться вследствие применения только одного основания.

Пример. Всех жителей России на первом этапе деления можно разделить по национальности на русских, белорусов, украинцев и т.д.; на втором этапе всех русских – на блондинов и брюнетов; на третьем этапе всех блондинов – на спортсменов и неспортсменов. Но нельзя на одном и том же этапе всех жителей России разделить на русских, блондинов и спортсменов.

Однако такого рода ошибки нередки и даже встречаются в сочинениях выдающихся мыслителей. Так, например, И. Кант в работе «Пролегомены ко всякой будущей метафизике, могущей появиться как наука» в логической таблице суждений делит все суждения в рамках одного этапа по качеству на утвердительные, отрицательные и бесконечные (13, с.121). Некорректность данного деления здесь заключается в том, что в нём утвердительные и отрицательные суждения действительно выделяются на основе признака качества суждения как основания деления, в то время как выделение бесконечных суждений подразумевает применение признака количества суждения как основания деления.

4. Правило последовательности и непрерывности деления. Это правило подразумевает выполнение следующего требования: на каждом этапе деления члены деления (видовые понятия) должны быть ближайшими видами по отношению к понятиям предшествующего этапа деления. При нарушении данного правила в процессе осуществления операции деления понятия возникает логическая ошибка, которая называется скачком в делении. Наличие этой ошибки демонстрирует прерывность и непоследовательность в осуществлении операции деления понятия.

Пример ошибки «скачок в делении». Пусть делимое понятие А есть понятие «число». Тогда представленная схема демонстрирует скачок в делении по двум правым ветвям следующей схемы:

Понятие «число»

понятие «действительное понятие «мнимое понятие «комплексное

число» число» число»

Скачок в делении здесь проявляется в том, что понятия «мнимое число» и «комплексное число» не являются ближайшими видами понятия «число», а являются ближайшими видами понятия «недействительное число», которое в представленной операции пропущено, что сигнализирует о наличии скачка в представленной операции деления.

Правильная операция деления понятия «число» должна осуществляться по следующей схеме: сначала на базе делимого понятия «число» должны быть выделены ближайшие видовые понятия «действительное число» и «недействительное число». Затем на базе понятия «действительное число» должны быть выделены ближайшие видовые понятия «рациональное число» и «иррациональное число». Соответственно на основе понятия «рациональное число» должны быть образованы ближайшие видовые понятия «целое число» и «дробное число», а на базе понятия «целое число» должны быть выделены ближайшие видовые понятия «целое положительное число» («натуральное число») и «целое отрицательное число». После этого на базе понятия «недействительное число» должны быть образованы ближайшие видовые понятия «мнимое число» и «комплексное число».

Схема правильного деления понятия «число».

«Число»

«действительное число» «недействительное число»

«рациональное «иррациональное «мнимое «комплексное

число» число» число» число»

«целое «дробное

число» число»

«положительное «отрицательное

целое число» целое число»

7.4.Понятие о классификации

Классификация есть мысленное распределение предметов по классам, образуемым на основе корректного осуществления операции деления некоторого общего понятия, существенного для науки либо практики.

Данное определение показывает, что в основе классификации как интеллектуальной операции лежит логическая операция деления и что процедурно классификация как приём познания ничем не отличается от операции деления понятия.

Различие между операцией деления понятия и классификацией усматривается в том, что операция деления понятия как операция, раскрывающая его объём, применяется к любым понятиям, в то время как классификация есть операция, раскрывающая объём понятий, существенных для науки либо практики. Как отмечает Е.К. Войшвилло, результаты деления понятий в классификациях входят в общий фонд человеческих знаний и постоянно сохраняются в нём (8, с. 210). Именно этим обстоятельством классификации отличаются от обычных делений понятий, которые можно назвать ситуативными, или рабочими, делениями понятий.

Так, например, в результате деления понятия «студент БФУ имени И. Канта 2011 года поступления» в объёме данного понятия можно выделить студентов, живущих в Центральном, Ленинградском, Балтийском районах г. Калининграда, и студентов, живущих за пределами г. Калининграда. Ясно, что данная информация лишь на короткое время представляет интерес для ректората БФУ им. И. Канта и она не войдёт в общий фонд человеческих знаний. Поэтому представленное деление понятия есть типичный пример ситуативного, или рабочего, деления понятия.

В то же время вышеописанное многоступенчатое деление понятия «число» представляет типичный пример классификации в математике; деление частей речи – типичный пример классификации в грамматике. Из школьного курса по биологии мы помним классификации животных и растений, предложенные Карлом Линнеем (1707 – 1778) и Жаном Батистом Ламарком (1744 – 1829), и т. д.

Все классификации в логике делятся на естественные (научные) и искусственные (вспомогательные). Естественные классификации – это классификации, в которых основаниями распределения предметов по классам являются существенные признаки, в разной степени присущие классифицируемым предметам.

Классическим примером естественной (научной) классификации является распределение химических элементов в таблице Д.И. Менделеева (1834 – 1907). Д.И. Менделеев заметил важный признак всех химических элементов: по мере нарастания их атомных весов они периодически меняют свои свойства от металлических к металлоидным. Как отмечает Е. К. Войшвилло, «с каждой рубрикой, выделяющей отдельный элемент, ряд или столбец этой таблицы … связана определенная совокупность знаний о соответствующих химических элементах» (8, с. 211).

Эвристический характер классификации химических элементов в таблице Д.И. Менделеева, равно как и других естественных классификаций, подчеркивают В.А. Бочаров и В.И. Маркин: «…Естественная классификация химических элементов, предложенная Д.И. Менделеевым (таблица Менделеева), позволяет по одному только местоположению того или иного элемента в таблице установить огромное число его свойств, предсказать поведение этого элемента в самых различных химических реакциях. То же самое характерно и для современной классификации биологических организмов» (4, с. 196).

Искусственная (вспомогательная) классификация не решает познавательные задачи, она предназначена для решения практических задач.

Искусственная (вспомогательная) классификация – это такая классификация, в которой основанием распределения предметов по классам выступает признак, который не является существенным для познания классифицируемых предметов, но является важным для систематизации их пространственного положения.

Классическим примером искусственной (вспомогательной) классификации является расстановка книг в библиотеке на книжных стеллажах в алфавитном порядке (по первым буквам фамилий их авторов). Понятно, что данный признак не несёт никакой информации о содержании книг, однако классификация книг по данному признаку в целях последовательного расположения книг на книжной полке делает удобным, быстрым и лёгким процесс отыскания любой книги из числа имеющихся в библиотеке для передачи её читателю.

Иногда термин «искусственная классификация» применяют к неадекватным классификациям, изначально предназначенным для решения познавательных задач. Именно так оценивают В.А. Бочаров и В.И. Маркин классификацию биологических организмов, предложенную в XIX веке К. Линнеем, так как в отличие от классификации химических элементов Д.И. Менделеева, обладающей большим эвристическим потенциалом, классификация организмов К. Линнея «этой особенностью не обладала» (4, с.196).

В заключение отметим, что теперь мы имеем полное и достаточно ясное представление о понятии как форме мышления, и если учесть, что понятия являются структурными элементами другой, более сложной формы мышления, которая называется суждением, то это позволит нам с необходимой ясностью и полнотой познать суждение как форму мышления.