Прочность наклонных сечений на действие изгибающих моментов.

Расчет на действие момента производится для наклонных сечений в местах обрыва продольной арматуры, у граней свободной опоры балок, у свободного конца консоли при отсутствии у продольной арматуры специальных анкеров, а также в местах резкого изменения высоты сечения.

Расчет производят из условия

M ≤ M_s + M_sw

М – момент от внешних сил,

M_s – момент, воспринимаемый продольной арматурой, пересекающей наклонное сечение, относительно противоположного конца наклонного сечения,

M_sw –момент, воспринимаемый поперечной арматурой, пересекающей наклонное сечение, относительно противоположного конца наклонного сечения.

M_sw = N_sz_s,

Здесь

N_s - усилие в продольной растянутой арматуре N_s = R_sA_s,

z_s - плечо внутренней пары z_s = h₀ - (N_s/2R_bb).

При наличии сжатой арматуры z_s ≥ h₀-a'.

Допускается принимать z_s = 0,9h₀.

Момент M_sw при наличии хомутов определяют по формуле

M_sw = 0,5q_swс². (2.46)

В этой формуле q_sw определяется по формуле (2.39), а «с» ≤2h₀.

При пересечении наклонного сечения с продольной арматурой, не имеющей анкеров в пределах зоны анкеровки, усилие N_s должно определяться с учетом уменьшения расчетных напряжений.

Пример 5.1.Определить диаметр и шаг поперечных стержней для железобетонной балки прямоугольного сечения. Размеры сечения b×h= 20×60 см, (0,2×0,6м). Бетон класса В20; R_b =11,5 МПа, (11,5·10³ кН/м²);R_bt= 0,9 МПа, (0,9·10³ кН/м²); арматура хомутов класса А240, R_sw= 170 МПа, (170·10³ кН/м² ); постоянная нагрузка от собственного веса g = 15 кН/м; временная равномерно распределенная q_v = 30 кН/м. Полная нагрузка q = q_v + q_g = 30+15 = 45 кН/м. Наибольшая поперечная сила Q_мах = 180 кН. Защитный слой а= 6 см.

Рабочая высота сечения

h_o =h – а = 60 – 6 = 54см = 0,54 м.

Вычисляем усилие, воспринимаемое бетоном.

М_в= 1,5R_btb h_o²=1,5·0,9·10³·0,2·0,54² = 78,73 кНм.

Нагрузка qсодержит временную нагрузку, которая приводится к эквивалентной равномерно распределенной нагрузке

q₁ = q – 0,5q_v = 45 – 0,5∙30 = 30 кН/м.

Условная поперечная сила, воспринимаемая бетоном (2.28).

Q_в1 = 2√ М_в ·q₁ = 2√ 78,73 ∙30 = 97,2 кН.

Проверяем неравенство

Q_b1 < (2М_в/ h_o) - Q_max = 97,2 кН < (2∙78,73 / 0,54) - 180 = 111,6 кН.

Вычисляется интенсивность погонной нагрузки на хомуты

q_sw = (Q_мах - Q_в1)/1,5h_o = (180 – 97,2) / 1,5∙0,54 = 102,2 кН/м.

В железобетонных элементах, в которых поперечная сила по расчету не может быть воспринята только бетоном, следует устанавливать поперечную арматуру с шагом не более 0,5h_o и не более 300 мм.

S₁ ≤ 540/2 = 270 мм, S₁ ≤ 300мм.

Максимально допустимый шаг поперечных стержней

s_мах = R_bt·b h_o² / Q_мах = 0,9·10³·0,2·0,54²/180 =0,290 м = 29 см.

Назначаем, предварительно, шаг хомутов S₁ = 200 мм.

Необходимая площадь сечения поперечных стержней при s₁ = 250 мм.

Рис. 2.8. Поперечное армирование элемента 1 – АSW = 2Ø12 А240, S1 = 200 мм, S2 = 250 мм.

а = 60

b = 200

аt=15

ц.т

dw=10

q = v + g = 30 + 15 = 45 кН/м

S2

S2

S2

S2

S2

S1

S1

S1

S1

S1

n1·S1

l/2

Qmax = 180 кН

n2·S2

Аs

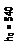
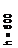
A_sw = q_sw·s₁ / R_sw= 102,2 ·0,25 /170·10³ = 1,50·10^{-4 м2} = 1,50 см².

Принимаем в сечении 2Ø10 А240 с A_sw = 1,57 см².

Реальная погонная нагрузка на хомуты у опоры

q_sw = R_sw· A_sw / s₁ = 170·10³·1,57·10^-4/0,25 = 106,76 кН/м.

Проверяем условие

q_sw ≥ 0,25 R_btb

q_sw = 106,76 кН/м > 0,25∙0,9·10³∙0,2 = 45 кН/м.

Условие удовлетворяется, уточнения расчета не требуется.

Окончательно, принимаем для хомутов 2Ø12 А240 с A_sw= 1,57 см² с шагом в приопорных зонах 200 мм, а в пролете 250 мм. Схема армирования сечения представлена на рис.2.8.

Пример 5.2.Для балки прямоугольного сечения выполнить проверку прочности наклонного сечения по поперечной силе при следующих данных.

Размеры поперечного сечения b×h = 30×85 см, (0,3×0,85 м). Бетон тяжелый класса В20; R_b=11,5 МПа, (11,5·10³ кН / м² ); R_bt = 0,9 МПа, (0,9·10³ кН / м² ); арматура хомутов класса А240, R_sw = 170 МПа, (170·10³ кН / м²); шаг хомутов у опоры s= 25 см, число хомутов в поперечном сечении n = 3, диаметр хомутов 8 мм, постоянная нагрузка от собственного веса q_g = 20 кН/м; временная равномерно распределенная (эквивалентная) q_v = 40 кН/м. Наибольшая поперечная сила на опоре Q_мах = 360 кН. Защитный слой, а = 5 см.

Рабочая высота сечения h_o=h – а = 85 – 5 = 80 см = 0,80 м.

Проверка прочности наклонного сечения на действие поперечной силы по наклонной трещине производится из условия

Q ≤ Q_в + Q_sw..

Определяем интенсивность хомутов

q_sw = R_sw A_sw / s_w = 170·10³·3∙0,503·10^-4/0,25 = 102,61кН/м.

Проверяем необходимость учета хомутов в расчете по условию

q_sw ≥ 0,25 R_btb

q_sw/ R_bt·b = 102,61/0,9·10³∙0,3 = 0,38 > 0,25.

Условие выполняется, хомуты учитываются в расчете полностью.

М_в= 1,5R_btbh_o²=1,5·0,9·10³·0,3·0,8² = 259,2 кНм.

Полная расчетная нагрузка q₁ = q_v+q_g= 40+20 = 60кН/м.

Вычисляется отношение

√ М_в / q₁ = √259,2/60 = 2,08 м,

2h_o/(1 – 0,5q_sw/ R_bt·b) = 2∙0,8/(1- 0,5∙0,38) = 1,975м.

Проверяем условие

Qmax = 360 кН

n2·S2

n1·S1

Рис. 2.9. Поперечное армирование изгибаемого элемента к примерам 5.1 и 5.2. 1- АS = 3Ø8 А240, S1 = 250 мм, S2 = 500 мм.

а = 50

b = 300

аt=15

dw=8

q = v + g = 40+20 = 60 кН/м

S2

S2

S2

S2

S2

S1

S1

S1

S1

S1

l/2

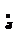
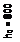
√ М_в / q₁ = 2,08 м > 2h_o/(1 – 0,5q_sw/ R_btb) = 1,975м.

Следовательно, длина проекции невыгоднейшего наклонного сечения вычисляется по формуле

с = √ М_в / q₁ = √259,2/60 = 2,08 м, но не более 3h_o= 3∙0,8 = 2,4 м.

с = 2,08м > с₀= 2h_o= 1,6м.

Для дальнейших расчетов принимаем с = с₀ = 1,6м.

Q_sw = 0,75q_sw с₀ = 0,75∙102,61∙1,6 =123,132кН.

Q_в = М_в /с = 259,2/1,6 = 162,0кН.

Q = Q_max- q₁c = 360 - 60∙1,6 = 264 кН.

Проверяем условие прочности

Q = 264 кН < Q_в + Q_sw =162,0 + 123,132 = 285,132кН.

Прочность наклонных сечений обеспечена.

Схема армирования сечения представлена на рис. 5.1.

Пример 5.3. Для балки с данными, изложенными в примере 5.2, проверить прочность бетонной полосы между наклонными трещинами.

Q = 360кН < 0,3R_bbh_o = 0,3∙11,5·10³∙0,3∙0,85 = 879,75кН.

Прочность наклонной полосы обеспечена.

Задание. 5. В соответствии с данными таблицы 5 выполнить расчет прочности наклонного сечения балки прямоугольного профиля. Определить диаметр и шаг поперечных стержней. Законструировать сечение с соблюдением конструктивных и нормативных требований. Выполнить чертежи армирования в масштабе 1:10 или 1:25.

Таблица 5

№	Расчетная поперечная сила Q кН	Размеры сечения см	Расчетная нагрузка кН/м	Класс арматуры	Класс бетона
Высота h	Ширина b	Постоянная qg	Временная qv
						А240	В25
						А240	В25
						А240	В25
						А240	В25
						А240	В25
						А240	В25
						А240	В25
						А240	В30
						А240	В30
						А240	В30
						А240	В30
						А240	В30
						А240	В30
						А240	В30
						А240	В30
						А240	В30
						А240	В30
						А240	В30
						А240	В30
						А240	В30
						А240	В35
						А240	В35
						А240	В35
						А240	В35
						А240	В35

Задание 6. Сжатые железобетонные элементы прямоугольного профиля

Расчет элементов прямоугольного сечения с арматурой, расположенной у перпендикулярных плоскости изгиба граней, допускается производить по предельным усилиям. При расчете внецентренно-сжатых элементов необходимо учитывать величины реальных и случайных эксцентриситетов, а также влияние прогибов на несущую способность. В зависимости от величины эксцентриситета условно различают:сжатие со случайными эксцентриситетами и сжатые с расчетными эксцентриситетами.