Кузнецов В.С. Шапошникова Ю.А.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение
высшего образования
НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ" (НИУ МГСУ)
Методические указания
кпрактическим занятиям
по дисциплине «Железобетонные и каменные конструкции»
Составители
Кузнецов В.С. Шапошникова Ю.А.
Москва 2015
Оглавление
Введение………………………..
1. Занятие.1. Основные положения расчетов прочности……..
1.1. Нагрузки на строительные конструкции……………
1.2. Основные положения статического расчета ………..
1.3. Сущность железобетона………………………………
1.4. Прочность бетона и арматуры……………………….
1.5. Примеры расчета…………………………………………
2. Занятие 2. Прочность изгибаемых элементов прямоугольного профиля
2.1. Прочность нормальных сечений с одиночной арматурой……
2.2. Проверка прочности сечений с одиночной арматурой………
2.3. Примеры расчета…………………………………………
3. Занятие 3. Прочность элементов таврового профиля…………………..
3.1. Нейтральная ось в полке………………………………………
3.2. Нейтральная ось в полке………………………………………
3.3. Примеры расчета………………………………………………
4. Занятие 4. Прочность нормальных сечений с двойной арматурой……
4.1. Расчет прочности нормальных сечений ……………………
4.2. Проверка прочности нормальных сечений………………..
4.3. Примеры расчета………………………………………………
5. Занятие 5. Изгибаемые элементы.Прочность наклонных сечений…
5.1. Подбор вертикальных стержней…………………………………
5.2. Проверка прочности наклонных сечений………………………..
5.3. Примеры расчета……………………………………………..
6. Занятие 6. Прочностьсжатых железобетонных элементов…………
6.1. Элементы, сжатые со случайными эксцентриситетами……
6.1. Элементы, сжатые с расчетными эксцентриситетами……
6.3. Примеры расчета……………………………………………
Контрольные вопросы……………………………………………
Литература……………………………………………………………..
Практический расчет железобетонных и каменных конструкций
Данный материал предназначен для проведения практических занятий со студентами, обучающимися по программе бакалавров и, включает расчеты прочности и конструирования изгибаемых и сжатых элементов с учетом требований современной нормативной базы. Приводится сводка необходимых расчетных формул и пояснений к ним.
1. Занятие. Основные положения расчетов прочности
Для того чтобы спроектировать здание или сооружение или какой либо отдельный элемент необходимо знать какие нагрузки будут приложены, их величины, продолжительность действия и совместность действия, конструктивную и расчетную схемы, прочностные характеристики материалов.
Нагрузки на строительные конструкции
Все нагрузки и воздействия определяются в соответствии с СП 20.13330.2011 «Нагрузки и воздействия». Актуализированная версия [1].
Постоянные нагрузки- это собственный вес железобетонных конструкций, вес и давление грунта, гидростатическое давление, усилие преднапряжения. Вес железобетонных конструкций устанавливается по фактическим размерам изделий, их реальной средней плотности или по каталогу.
Временные нагрузки - снеговые, ветровые, полезные (технологические) и т.д.
Величина полезной (технологической) нагрузки приводится в задании на проектирование или определяются по нормам. При определении усилий в элементах здания необходимо учитывать снижение нагрузки вследствие неравномерности загружения перекрытий на всех этажах здания.
Таблица 1.1.
Снеговая нагрузка определяется в соответствии с выбранным районом строительства, с учетом изменения величины нагрузки за счет ветра и профиля кровли. Полное нормативное значение снеговой нагрузки на горизонтальную проекцию покрытия определяется по формуле
s = s0·μ·се, (1.1)
Где
s0 – нормативное значение веса снегового покрова на 1м2 поверхности земли, в соответствии с заданным районом,
μ – коэффициент перехода от веса снегового покрова на 1м2 поверхности земли к весу снеговой нагрузки на покрытие (для плоских кровель μ = 1),
се– коэффициент снижения снеговой нагрузки в (районах со средней скоростью ветра v ≥ 2 м/сек за три наиболее холодных месяца, определяемый по формуле
Таблица 1.2
| Снеговой район | I | II | III | IV | V | VI | VII | VIII |
| S0 кН/м2(кгс/м2) | 0,8 | 1,2 | 1,8 | 2,4 | 3,2 | 4,0 | 4,8 | 5,6 |
се = (1,2 – 0,1v√ k)(0,8 + 0,002b), (1.2)
где
k – коэффициент, учитывающий изменение ветрового давления по высоте,
b – ширина покрытия, принимаемая не более 100 м.
Для снеговой нагрузки длительная часть учитывается в районах со средней температурой января минус 50С и составляет 70% от полной.
Ветровая нагрузка определяется в соответствии с выбранным районом строительства, высотой над поверхностью земли, типа местности, конфигурации объекта и т.д.
Таблица 1.3
| Ветровой район | Ia | I | II | III | IV | V | VI | VII |
| W0 кН/м2(кгс/м2) | 0,17 | 0,23 | 0,3 | 0,38 | 0,48 | 0,6 | 0,73 | 0,85 |
| W0 |
При проектировании железобетонных конструкций используются нормативные и расчетные значения нагрузок.
Нормативные постоянные нагрузки принимаются по фактическим размерам и средним величинам плотностей; нормативные временные нагрузки определяются по фактическим данным или среднестатистическим значениям.
Расчетное значение нагрузки определяется произведением ее нормативного значения на коэффициент надежности по нагрузки γf , который зависит от вида нагрузки и выполняемого расчета.
Например, для расчетов по первой группе предельных состояний (расчеты на прочность), коэффициенты надежности составляет:
γf =1,1 – масса железобетонных конструкций, (плотность > 1600 кг/м3 ),
γf =1,2 – при полезных нагрузках 2,0 и более кПа.
При расчете железобетонных конструкций и оснований учитывают коэффициент надежности проектируемого здания по степени ответственности γn.
Прочие временные нагрузки
· Нагрузки от транспортных средств,
· Нагрузки от мостовых кранов,
· Гололедные нагрузки
· и др.
Задание 1.1 Записать значения расчетных нагрузок для:
· Бетонных конструкций (γ ≤ 1600кг/м3), выполняемых на стр. площадке,
· Полной временной полезной нагрузки на лестницы биллиардной,
· Пониженной временной полезной нагрузки на лестницы биллиардной,
· Полной снеговой для IV снегового района,
· Пониженной снеговой для IV снегового района,
· Ветровой для IV ветрового района на высоте 20 м и типе местности В,
· Распределенную нагрузку от транспорта на пандусы от а/м весом до 3тс.
Сущность железобетона.
Расчет прочности нормальных сечений изгибаемых элементов заключается в определении необходимого количества растянутой арматуры, в предположении, что прочность бетона сжатой зоны и продольной растянутой арматуры в рассматриваемом сечении будет исчерпана одновременно.
| Рис.1. Изгибаемый железобетонный элемент 1-арматура, 2- нормальные трещины, 3- нейтральная ось, 4- арматура |
| σ |
| τ |
| а- а |
| а |
| а |
| q |
| М |
| Q |
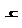
Если в балку в растянутую зону уложить небольшое количество арматуры, то несущая способность элемента повышается в несколько раз, по сравнению с неармированным образцом.
| N1 >> N2 |
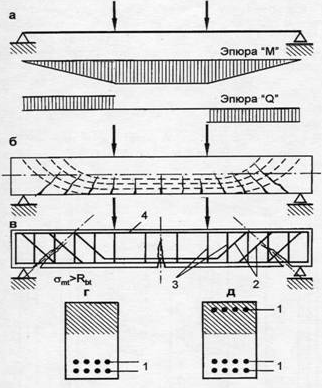
При размещении арматуры в сжатых элементах, несущая способность последних может увеличиваться до 50%, поскольку сопротивление арматуры сжатие в несколько раз превосходит аналогичный показатель для бетона. Так 1см2, широко распространенной арматуры класса А400 заменяет 24,5 см2 бетона класса В25.
Прочность бетона и арматуры
Прочность бетона характеризуется классами бетона на сжатие В и на растяжение Bt. Например: В20 или В40. Чем больше цифра, тем прочнее бетон. Для расчетов прочности используются расчетные значения прочности на сжатие и растяжение, которые привязаны к классу бетона и указаны в СП 52-01-2003. Бетонные и железобетонные конструкции. Основные положения. Актуализированная версия. М., 2012.
Таблица 1.4
| Класс бетона В | Сжатие осевое, МПа | Растяжение осевое, МПа | Модуль упругости, МПа | ||
| Rbn | Rb | Rbt,n | Rbt | Eb | |
| В25 | 18,5 | 14,5 | 1,55 | 1,05 | 30,0∙103 |
| В35 | 25,5 | 19,5 | 1,95 | 1,30 | 34,5∙103 |
Задание 1.3.Для тяжелого бетона классов В20, В40, В60 и В80 выписать значения прочности на сжатие Rbи растяжениеRbt.
Прочность арматуры характеризуется классами арматуры, обозначаемыми буквами А – стержневая арматура, В проволочная арматура, К – высокопрочные канаты. Например: А400, В500 или К1500. Чем больше цифра, тем прочнее арматура. Для расчетов прочности используются расчетные значения прочности арматуры на растяжение Rs или на сжатие Rsс, которые привязаны к классу бетона и указаны в СП 52-01-2003. Бетонные и железобетонные конструкции. Основные положения. Актуализированная версия. М., 2012.
Задание 1.4.Для Арматуры классов А240, А800, В500 и К1400 выписать значения прочности на сжатие Rscи растяжениеRs.
Пример расчета
Пример 2.1. Выполнить расчет прочности сечения с одиночной арматурой. Размеры сечения b×h = 40×140см, бетон В20; Rb =11,5 МПа, (11,5·103 кН/м2); рабочая арматура класса А400, Rs =355 МПа, (355·103 кН/м2); в сечении действует расчетный момент (с учетом кратковременных нагрузок) М = 600 кНм. Предварительное расположение стержней в один ряд, а=4 см.
Рабочая высота сечения ho=h – а = 140 – 4 = 136 см=1, 36 м.
Граничная высота сжатой зоны при арматуре А400
ξR =0, 531, αR = 0,39.
Вычисляется коэффициент αm
αm = М / Rbbho2 = 600 / 11,5·103 ·0,4·1,362 = 0,0705.
αm = 0,0705< αR = 0,390.
| а = 60 |
| b = 400 |
| а2 =310 |
| a6 =334 |
| аt=15 |
| ц.т |
| dw=8 |
| Рис. 2.1. Армирование сечения изгибаемого элемента к примеру 2.1. 1 –2Ø22 А400 АS = 7,6 см2, 2–2Ø20 А400 АS = 6,28 см2, 3–2Ø10 А400 А/S = 1,57 см2, 4–AS1= 0,1·0,25h·0,5b = 0,7 см2. 1Ø10 А400 AS1=0,785 см2. |
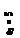
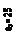
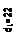
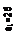
Сжатая арматура по расчету не требуется. Вычисляется площадь растянутой арматуры
As=Rbbh0 (1-√1-2αm)/Rs =11,5·103 ·0,4·1,36(1-√1- 2·0,0705)/355·103 ≈ 0,00129 м2 =12,9 см2.
В соответствии с сортаментом принимаем
2Æ20+2Æ22 А400 с площадью Аs = 6,28+7,6 = 13,88 см2.
При размещении арматуры в два ряда рабочая высота сечения уменьшится и будет равна, см. рис. 2.1.
ho= h – а-Ø/2-а1 /2=140 – 4 –22/2 –25/2 = 133,5см ≈134,0 см=1, 34 м,
где а1 – минимальное расстояние между продольными стержнями а1= 25мм.
Уточним расчет при ho = 1,34 м.
αm = М / Rbbho2 = 600/11,5·103 ·0,4·1,342 = 0,0726.
αm = 0,0726 < αR = 0,390.
Сжатая арматура по расчету не требуется. Уточняем площадь растянутой арматуры
As= Rbbh0(1-√1 -2αm)/Rs = 11,5·103 ·0,4·1,34(1-√1-2·0,0726)/355·103 =0,00131 м2 =13,1 см2 .
В соответствии с сортаментом принимаем
2Æ20 + 2Æ22 А400 с площадью Аs= 6,28+ 7,6 =13,88 см2.
Перерасход арматуры составляет (13,88 –13,1)·100/13,1 = 5,95%.
Процент армирования сечения
μ=100As/ bho=100·13,1/40·134 = 0,244% > μmin = 0,1%.
Схема армирования сечения представлена на рис. 2.1.
Задание. 2. В соответствии с данными таблицы 1 выполнить расчет прочности нормального сечения прямоугольного профиля с одиночной арматурой. Законструировать сечение с соблюдением конструктивных и нормативных требований. Выполнить чертежи армирования в масштабе 1:10 или 1:25.
| Рис.2.2. Армирование сечений к примеру 2.2. 1–4Ø18А400 АS=10,18 см2, 2–2Ø10 А400 А/S=1,57 см2, 3–4Ø10 А400 АS1=3,14 см2 |
| б) |
| b = 300 |
| а2 =218 |
| а6 =234 |
| аt=15 |
| ц.т |
| а = 60 |
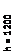
Пример 2.2.Выполнить проверку прочности нормального сечения элемента. Размеры поперечного сечения b× h=30×120 см. Тяжелый бетон класса В25; Rb =14,5МПа, (14,5·103 кН/ м2); рабочая арматура - стержни 4Æ18 А400 с площадью Аs= 0,18 см2 = 0,001018 м2, Rs= 355 МПа, (355·103 кН /м2 ); в расчетном сечении действует внешний изгибающий момент от всех нагрузок, включая кратковременные, М = 350 кНм, а= 6 см. Рабочая высота сечения ho=h –а=120 – 6 =114см=1,14 м.
Положение нейтральной оси, значение «х»
х = Rs As/Rbb = 355·103 · 0,001018 / 14, 5·103·0,3 = 0,0831м = 8,31см.
Для арматуры А400 находим ξR = 0,531, αR = 0,390.
ξ = х/h0 = 8,31/114 = 0,0729 < ξR = 0,531.
Проверка прочности нормальных сечений с одиночной арматурой производят при ξ ≤ ξR из условия
Мсеч= RsAs(h0 – 0,5х) = 355·103 ·0,001018 (1,14 – 0,5·0,0831) =396,96 кНм.
М = 350 кНм ≤ Мсеч= 396,96 кН·м.
Условие прочности выполняется, прочность сечения достаточна.
Коэффициент армирования сечения
μ = As/ b·ho = 10,18/30·114 = 0,00297, (0,3%) > μmin = 0,1%.
Схема армирования поперечного сечения представлена на рис. 2.2.
Таблица 2.1
| № | Момент | Высота сечения h | Ширина сечения b | Класс бетона | Класс арматуры |
| кНм | см | см | |||
| В25 | А400 | ||||
| В25 | А400 | ||||
| В25 | А400 | ||||
| В25 | А400 | ||||
| В25 | А400 | ||||
| В25 | А400 | ||||
| В25 | А400 | ||||
| В30 | А500 | ||||
| В30 | А500 | ||||
| В30 | А500 | ||||
| В30 | А500 | ||||
| В30 | А500 | ||||
| В30 | А500 | ||||
| В30 | А500 | ||||
| В30 | А400 | ||||
| В30 | А400 | ||||
| В30 | А400 | ||||
| В30 | А400 | ||||
| В30 | А400 | ||||
| В30 | А400 | ||||
| В35 | А400 | ||||
| В35 | А500 | ||||
| В35 | А500 | ||||
| В35 | А500 | ||||
| В35 | А500 |
3. Занятие 3. Изгибаемые элементытаврового профиля.
Задание 4. Изгибаемые элементы прямоугольного профиля
Прочность наклонных сечений
Проверку прочности наклонного сечения необходимо производить.
· По сжатой бетонной полосе между наклонными сечениями.
· На действие поперечной силы по наклонному сечению.
· На действие изгибающего момента по наклонному сечению.
Задание 6. Сжатые железобетонные элементы прямоугольного профиля
Расчет элементов прямоугольного сечения с арматурой, расположенной у перпендикулярных плоскости изгиба граней, допускается производить по предельным усилиям. При расчете внецентренно-сжатых элементов необходимо учитывать величины реальных и случайных эксцентриситетов, а также влияние прогибов на несущую способность. В зависимости от величины эксцентриситета условно различают:сжатие со случайными эксцентриситетами и сжатые с расчетными эксцентриситетами.
Пример 6.1.
| Рис. 6.1. Армирование сжатого элемента к примеру 6.1. 1 – 2Ø16 А400 АS= 4,02 см2, 2 – 4Ø8 А240 АS1 = 2,01 см2. |
| 1 - 1 |
Определить площадь арматуры в сечении сжатого элемента. Продольная сила действует на колонну со случайными эксцентриситетами, сечение - прямоугольное с размерами b× h = 40×40 см. Бетон класса В20, Rb= 11,5 МПа, (11, 5·103 кН/м2), рабочая арматура класса А400, Rs = Rsс = 355 МПа, (355·103 кН/м2 ). Расчетная продольная сила N =1800кН; длительно действующая часть Nl = 900кН; эксцентриситет приложения силы е0 = еа, η =1,0; l0 = 6,0 м. Вычисляем гибкость элемента λ = l0 / h = 600/40 = 15 < 20.
По таблице 8 приложения при Nl / N = 900/1800 = 0,5 и l0 / h =15 находятся коэффициенты φb = 0,84 и φsb = 0,875.
Принимаем μ + μ´= 1,0% и находим коэффициент αs
αs=Rsс μ/ Rb=355·103 ·0,01/11, 5·103 = 0,309.
Уточняется значение φ
φ= φb + 2(φsb – φb) αs= 0,84 + 2(0,875 – 0,84)0,309 = 0,861.
Находится суммарная площадь арматуры
Аs+А´s= (N/φ·Rsс) – (bhRb /Rsс) =(1800/0,861·355·103 ) - (0,4·0,4·11,5·103 /355·103) = 0,000706м2 = 7,06см.2
Коэффициент армирования μ + μ´= 14,12 / 40·40 = 0,00883
μ + μ´= 0,00883 больше μ min + μ´ min = 0,001.
Уточнения площади арматуры не требуется, поскольку полученное значение 0,00883 не отличается существенно от заданного.
Окончательно, принимаем арматуру
4Ø16 А400, Аs + А´s = 8,04 см2.
Схема армирования сечения представлена на рис. 6.1.
Пример 6.2.Определить количество арматуры при следующих данных.
Колонна связевого каркаса с размерами b×h= 40×40 см. Бетон тяжелый В20, Rb =11,5 МПа, (11,5·103 кН/м2), Ев = 27,5·103 МПа (27,5·106кН/м2); рабочая арматура класса А400, Rs = Rsс = 355 МПа, (355·103 кН / м2 ), Es= 2·105 МПа (2·108 кН/м2). Высота этажа 3,2м, защитный слой а = а´= 4 см, расчетная длина колонны равна высоте этажа l0 = 3,2м.
В расчетном сечении действуют усилия только от вертикальных нагрузок.
От постоянных, длительных и временных вертикальных нагрузок продольная сила NV= 400кН, момент Mv= 100кНм.
От постоянных и длительных вертикальных нагрузок продольная сила Nl= 300 кН, момент Ml= 50кНм.
Рабочая высота сечения
ho = h – а= 40 – 4=36см = 0,36 м.
Определяем отношение l0/h = 3,2 /0,4 = 8 > 4, обязателен учет гибкости.
Вычисляется жесткость элемента D при учете полных нагрузок, т.е.
М = 100кНм, N = 400 кН.
Эксцентриситет е0 = M/N = 100/400 = 0,25м = 25,0 см.
ea ≤ 10 мм; ea ≤ h/30 = 40/30 = 1,33см; еa ≤ l/600 = 3,2/600 = 0,53 см.
е0 = 25,0 см > еа = 1,33см;
Таким образом, изгибающий момент не уточняется.
М1 = М + N(h0 - a')/2 = 100 + 400(0,36 – 0,04)/2 = 164 кНм.
М1l = М l + N l (h0 - a') / 2 = 50 + 300(0,36 – 0,04)/2 = 98,0 кНм.
φl = 1+ М1 / М1l = 1+ 98,0/164 = 1,60 < 2,0.
δе = е0 / h0 = 25,0 /36 = 0,694 > 0,15. Принимаем δе = 0,694.
Коэффициент приведения арматуры к бетону
α = Es /Ев = 2·105 / 27,5·103 = 7,27.
Предварительно зададимся коэффициентом армирования μ = 0,015.
Вычисляем коэффициент μα. μα = 7,27·0,015 = 0,1091.
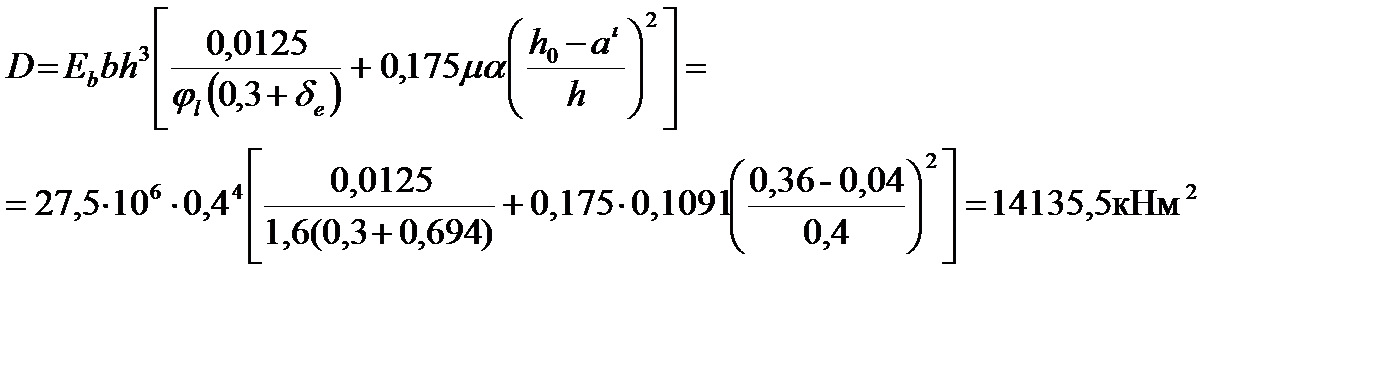
Находится величина критической силы
Ncr = π2D /l02 = 3,142·14135,5 / 3,22 = 13610,4 кН.
Коэффициент, учитывающий влияние прогибов колонны
ηv = 1/(1- N/Ncr) = 1/(1- 400/13610,4) =1,03.
Момент, с учетом влияния прогиба
М = Mv ηv = 100·1,03 = 103 кНм.
Для установления количества арматуры произведем промежуточные вычисления.
δ =a' / h0 = 4 /36 = 0,111,
αn = N / Rbbh0 = 400/11,5·103·0,4·0,36 = 0,242,
ξR = 0, 531; αR = 0,390.
| 1 – 1 |
| Рис.2.10. Армирование сжатого элемента к примеру 2.11. 1 – 2Ø14 А400 АS=3,08 см2, 2 – 1Ø12 А300 АS=1,131см2, 3 – 4Ø8 А240 АSW=2,01 см2. |
Поскольку αn = 0,242 < ξR = 0, 531, количество арматуры определяем по формуле
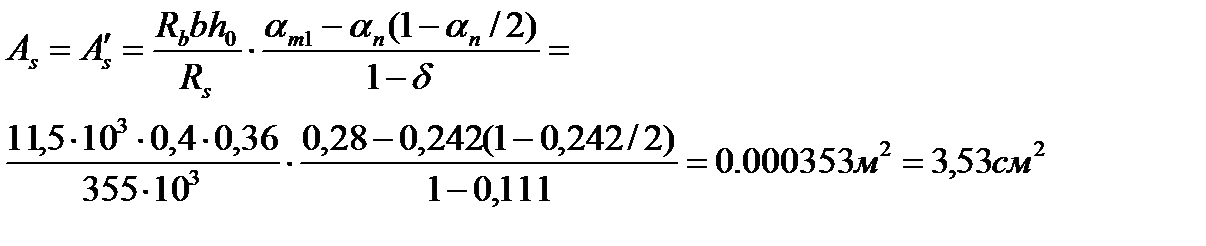
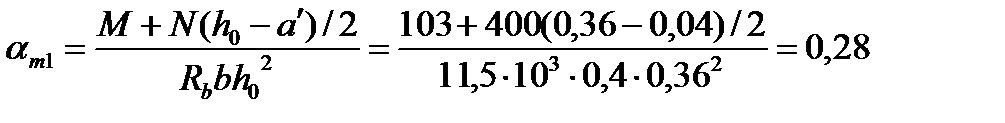Принимаем для армирования As = A's = 2Ø14 +1Ø12 А400 с общей площадью сечения арматуры 3,08 +1,131 = 4,211см2. Схема армирования сечения представлена на рис. 6.2.
В соответствии с данными таблицы 6.1 выполнить расчет прочности сжатого со случайными эксцентриситетами элемента прямоугольного профиля. Определить требуемое количество продольной арматуры. Законструировать сечение с соблюдением конструктивных и нормативных требований. Выполнить чертежи армирования в масштабе 1:10 или 1:25.
Таблица 6.1
| № | Расчетная продольная сила кН | Высота сечения h см | Ширина сечения b см | Класс бетона | Класс арматуры | |
| Полная N | Длительная Nl | |||||
| В25 | А400 | |||||
| В25 | А400 | |||||
| В25 | А400 | |||||
| В25 | А400 | |||||
| В25 | А400 | |||||
| В25 | А400 | |||||
| В25 | А400 | |||||
| В30 | А500 | |||||
| В30 | А500 | |||||
| В30 | А500 | |||||
| В30 | А500 | |||||
| В30 | А500 | |||||
| В30 | А500 | |||||
| В30 | А500 | |||||
| В30 | А400 | |||||
| В30 | А400 | |||||
| В30 | А400 | |||||
| В30 | А400 | |||||
| В30 | А400 | |||||
| В30 | А400 | |||||
| В35 | А400 | |||||
| В35 | А500 | |||||
| В35 | А500 | |||||
| В35 | А500 | |||||
| В35 | А500 |
В соответствии с данными таблицы 6.2 выполнить расчет прочности сжатого с расчетными эксцентриситетами элемента прямоугольного профиля. Определить требуемое количество продольной арматуры. Законструировать сечение с соблюдением конструктивных и нормативных требований. Выполнить чертежи армирования в масштабе 1:10 или 1:25.
Таблица 6.2
| № | Расчетная продольная сила кН | Расчетный момент кНм | Высота сечения h см | Ширина сечения b см | Класс бетона | Класс арматуры | ||
| Полная N | Длит. Nl | Полный М | Длит. Мl | |||||
| В25 | А400 | |||||||
| В25 | А400 | |||||||
| В25 | А400 | |||||||
| В25 | А400 | |||||||
| В25 | А400 | |||||||
| В25 | А400 | |||||||
| В25 | А400 | |||||||
| В30 | А500 | |||||||
| В30 | А500 | |||||||
| В30 | А500 | |||||||
| В30 | А500 | |||||||
| В30 | А500 | |||||||
| В30 | А500 | |||||||
| В30 | А500 | |||||||
| В30 | А400 | |||||||
| В30 | А400 | |||||||
| В30 | А400 | |||||||
| В30 | А400 | |||||||
| В30 | А400 | |||||||
| В30 | А400 | |||||||
| В35 | А400 | |||||||
| В35 | А500 | |||||||
| В35 | А500 | |||||||
| В35 | А500 | |||||||
| В35 | А500 |
Контрольные вопросы
1. Назовите классы тяжелого бетона на сжатие.
2. Назовите классы стержневой арматуры.
3. Какую часть от полной полезной нагрузки принимают как длительно-действующую.
4. Какую часть от полной снеговой нагрузки принимают как длительно-действующую.
5. В каких случаях сечение рассчитывается с двойной арматурой.
6. При расчете прочности ЖБЭ какие нагрузки используются: расчетные или нормативные?
7. При расчете прочности ЖБЭ какие характеристики бетона и арматуры используются: расчетные или нормативные?
8. Какие нагрузки больше расчетные или нормативные?
9. Какие характеристики бетона и арматуры больше: расчетные или нормативные?
10. Особенности разрушения изгибаемых элементов по нормальным сечениям. Граничное значение относительной высоты сжатой зоны сечений железобетонного элемента.
11. Проверка прочности о нормальным сечениям изгибаемых элементов прямоугольного профиля с одиночной арматурой. Подбор арматуры.
12. Подбор арматуры в изгибаемых элементах прямоугольного сечения по таблицам. Понятие о минимальном проценте армирования.
13. Проверка прочности по нормальным сечениям изгибаемых элементов прямоугольного профиля с двойной арматурой. Подбор арматуры.
14. Проверка прочности по нормальным сечениям изгибаемых элементов таврового сечения.
15. Подбор арматуры в изгибаемых элементах таврового сечения
16. Схемы разрушения изгибаемых элементов по наклонным сечениям. Расчет прочности по наклонным сечениям при действии изгибающего момента.
17. Расчет прочности изгибаемых элементов по наклонным сечениям при действии поперечной силы.
18. Особенности разрушения сжатых железобетонных элементов.
19. Прочность нормальных сечений внецентренно сжатых элементов и подбор арматуры.
20. Расчет прочности условно центрально сжатых элементов.
21. Учет случайных и расчетных эксцентриситетов.
22. Особенности расчета гибких сжатых элементов.
23. Расчет прочности центрально и внецентренно растянутых железобетонных конструкций.
24. Конструктивные требования по армированию изгибаемых и сжатых ЖБЭ.
Литература
Основная
1. Кузнецов В.С. Железобетонные и каменные конструкции. Учебник. АСВ, М.2015.
2. СП 20. 13330.2011 Свод правил. «Нагрузки и воздействия». Актуализированная версия к СНиП 2.01.07.85. М..,2011.
3. СП 52-01-2003. Бетонные и железобетонные конструкции. Основные положения. Актуализированная версия. М., 2012.
4. Кузнецов В.С. "Железобетонные конструкции многоэтажных зданий", М., АСВ, 2010.
Дополнительная
1. Байков В.Н., Сигалов Э.Е. “Железобетонные конструкции”, Общий курс, М., Стройиздат, 1991.
2. ГОСТ 10180-90. Бетоны. Методы определения прочности по контрольным образцам. М., 1990.
3. Кузнецов В.С., Малахова А.Н. "Железобетонные монолитные перекрытия и каменные конструкции многоэтажных зданий", М., АСВ, 2009.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение
высшего образования
НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ" (НИУ МГСУ)
Методические указания
кпрактическим занятиям
по дисциплине «Железобетонные и каменные конструкции»
Составители
Кузнецов В.С. Шапошникова Ю.А.
Москва 2015
Оглавление
Введение………………………..
1. Занятие.1. Основные положения расчетов прочности……..
1.1. Нагрузки на строительные конструкции……………
1.2. Основные положения статического расчета ………..
1.3. Сущность железобетона………………………………
1.4. Прочность бетона и арматуры……………………….
1.5. Примеры расчета…………………………………………
2. Занятие 2. Прочность изгибаемых элементов прямоугольного профиля
2.1. Прочность нормальных сечений с одиночной арматурой……
2.2. Проверка прочности сечений с одиночной арматурой………
2.3. Примеры расчета…………………………………………
3. Занятие 3. Прочность элементов таврового профиля…………………..
3.1. Нейтральная ось в полке………………………………………
3.2. Нейтральная ось в полке………………………………………
3.3. Примеры расчета………………………………………………
4. Занятие 4. Прочность нормальных сечений с двойной арматурой……
4.1. Расчет прочности нормальных сечений ……………………
4.2. Проверка прочно