Когда самоуверенность становится уголовным преступлением

Склонны ли люди к переоценке, если ставка превышает несколько долларов? Несмотря на то что соображения этического характера, очевидно, в ограниченных рамках можно исследовать в лабораторных условиях, есть по крайней мере одно свидетельство того, что переоценка может возникнуть, даже если на карту поставлена человеческая жизнь. Это свидетельство получено при исследованиях, связанных со смертной казнью.

В исчерпывающем обзоре несправедливых приговоров Хьюго Бедау и Майкл Раделет в 1987 году обсуждали 350 (275:) зафиксированных в США случаев, в которых ложно обвиненные в уголовных преступлениях, несмотря на то что обвинения «вызывали обоснованные сомнения», были осуждены. В пяти случаях ошибка была обнаружена до вынесения окончательного приговора. Другим обвиняемым повезло меньше: 67 были заключены в тюрьмы на срок до 25 лет, 139 — на срок более 25 лет и 139 были приговорены к смерти. На тот момент, когда Бедау и Раделет писали свой обзор, 23 человека из приговоренных уже были казнены.

Градуирование

«Градуирование» — это согласование уверенности и точности. Человек, принимающий решение, может считать свою градуировку совершенной, если во всех оценках уровня уверенности отношение точности равно вероятности правоты. Другими словами, 90% всех оценок верны — 90% уверенности в том, что ответы верны; 80% оценок верны — 80% уверенности в ответах и т.д.

Когда оценки индивидуальны, особого смысла говорить о градуировании нет. Насколько хорошо градуировано решение человека, ответившего 70% на вопрос п. 216 Анкеты? Градуировка важна, когда речь идет о сотнях оценок (Лихтенштейн, Фишхофф и Филлипс, 1982).

Поскольку существует множество способов измерения уверенности, существует ряд методик измерения градуировки. Одна из них — обычный подсчет разницы между средним уровнем уверенности и общей пропорцией правильных ответов. Скажем, человек имеет 80% уверенности в своих ответах на ряд вопросов из области общего знания, но правильно ответил только на 60%. Этот субъект переоценил свои силы на 20%.

Несмотря на то что такой способ градуирования очень удобен, он не всегда может быть применен. Представьте себе, например, человека, уверенность и точность оценок которого равны 80% каждая. Этот человек обладает совершенной градуировкой? Необязательно. Он мог быть на 60% уверен в половине ответов и на 100% — в другой половине (в среднем — 80% уверенности), а верно ответить на 80% вопросов и в первой, и во второй половине. Такой человек имеет заниженную самооценку, когда уверен в 60% ответов, и завышенную, когда уверен во всех. (276:)

Более совершенной методикой является оценка точности через ряд условий уверенности. Если точность подсчитывается для разных уровней уверенности, то появляется возможность создать «кривую градуирования», где горизонтальная ось будет обозначать уверенность, а вертикальная — точность. Рисунок 19.2 содержит две кривые градуирования: одна — для предсказания метеослужбами выпадения осадков, другая — для диагнозов пневмонии. Как вы можете видеть, предсказания погоды почти

Рисунок 19.2

Этот рисунок содержит кривые градуирования для прогнозов погоды (незакрашенные кружки) и диагнозов пневмонии (закрашенные кружки). В то время как прогнозы погоды почти безупречно проградуированы, врачи демонстрируют чрезмерную самоуверенность (при наличии или отсутствии у пациента пневмонии). Данные о прогнозах погоды взяты из отчета Аллана Мерфи и Роберта Уинклера (1984), а данные о врачах — из исследования Джей Кристенсен- Шалански и Джеймса Бушихеда (1981).

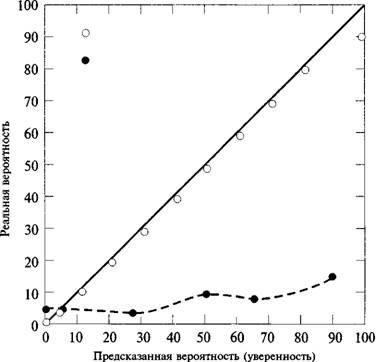
совершенно проградуированы, в среднем их прогнозы почти всегда совпадают с погодой (вопреки традиционным взглядам!). А вот диагнозы проградуированы очень плохо; большинство предсказаний этого характера лежат ниже линии, символизирующей совершенную градуировку.

Существует еще несколько способов оценивать градуировку, некоторые из них подразумевают хорошее знание математики. Например, одна из наиболее распространенных методик состоит в следующем: необходимо подсчитать так называемый «показатель Брайера» (названный по имени статистика Гленна Брайера). Показатель Брайера может быть разложен на три компоненты, одна из которых соотносится с градуировкой. Эта компонента числа Брайера представляет собой взвешенную среднюю величину между среднеквадратичными отклонениями пропорциональной точности во всех категориях и вероятности для каждой категории (более подробно см. Йетс, 1990).

Одна из наиболее интересных оценок градуировки известна как «индекс неожиданности». Индекс используется для оценок промежутков, точность которых известна. Например, представьте, что вы почувствовали 90%- ную уверенность в том, что правильный ответ на вопрос п. 12 Анкеты находится где- то между дюймом и милей (см. п. 126). Поскольку правильный ответ больше мили, этот ответ должен быть засчитан как неожиданность. Индекс неожиданности — это простое процентное выражение оценок, лежащих за границей уверенности.

В фундаментальном обзоре исследований градуирования Лихтенштейн, Фишхофф и Филлипс (1982) оценивали некоторые исследования, в которых респондентов просили указать интервалы, в которых они уверены на 98% (т.е. интервалы, которые с вероятностью 98% включали бы в себя верный ответ). В каждом исследовании ожидаемый индекс неожиданности составлял 2%. В среднем по данным всех экспериментов (всего около 15 000 оценок) индекс неожиданности составил около 32%. Другими словами, когда респонденты были уверены на 98%, что правильный ответ в названном ими промежутке, они оказывались правы на 68%. Еще раз переоценка подтвердила правило, а не исключение.

Склонны ли вы к переоценке? Эдуард Руссо и Поль Шумахер в 1989 году придумали легкий тест для самопроверки (см. рис. 19.3). Несмотря на то что исчерпывающая оценка градуировки (278:) требует сотен ответов, этот тест дает вам общее впечатление о том, каков ваш индекс неожиданности при ответе на вопросы из области общего знания при одном уровне уверенности. Руссо и Шумахер предложили этот тест более чем 1000 человек и обнаружили, что менее 1% респондентов смогли верно ответить на 9 или все 10 вопросов. Большинство людей неверно отвечали на 4- 7 вопросов (индекс неожиданности 40- 70%), опять- таки подтвердив свойство переоценки.