Проектирование верхней части колонны
Из таблицы 2 выбираем наиболее невыгодную комбинацию усилий:
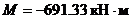 ;
; 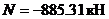 .
.
Вычисляем требуемую площадь поперечного сечения верхней части колонны:
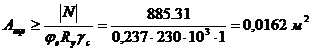 , где
, где
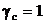 - коэффициент надежности по назначению.
- коэффициент надежности по назначению.
Для определения 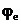 вычисляем предварительные характеристики сечения:
вычисляем предварительные характеристики сечения:
Предварительно вычисляем радиус инерции:
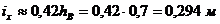 .
.
Ядровое расстояние:
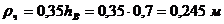 .
.
Условная гибкость:
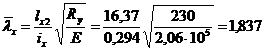 . Относительный эксцентриситет:
. Относительный эксцентриситет:
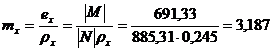 .
.
Задаемся отношением:
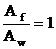 .
.
Приведенный относительный эксцентриситет:
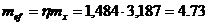 , где
, где
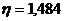 – коэффициент влияния формы сечения
– коэффициент влияния формы сечения
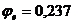 - коэффициент снижения расчетного сопротивления при внецентренном сжатии, по таблице 74 СНиП.
- коэффициент снижения расчетного сопротивления при внецентренном сжатии, по таблице 74 СНиП.
Производим компоновку поперечного сечения (рис.33).
Принимаем толщину полок:
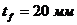 .
.
Высота стенки:
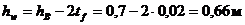 .
.
При 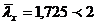 наибольшая условная гибкость:
наибольшая условная гибкость:
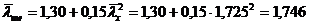 .
.
Из условия местной устойчивости (120) находим толщину стенки:
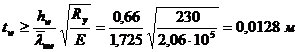 .
.
Поскольку сечение с такой стенкой неэкономично, принимаем толщину стенки tw = 10мм, у которой средняя часть теряет устойчивость, а в расчёте будут учитываться только пояса и примыкающие участки стенки длиной:
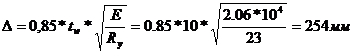
Требуемая площадь одного пояса составит:
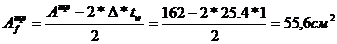
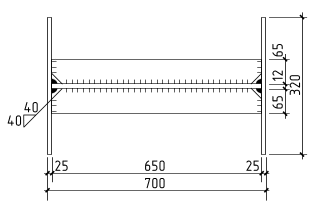
Рис.32. Сечение верхней части колонны.
Из условия устойчивости верхней части колонны из плоскости рамы:
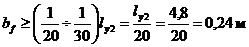 .
.
Принимаем 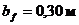 ;
;
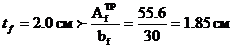 .
.
Проверяем пояс из условия обеспечения местной устойчивости:
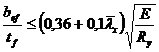 ;
;
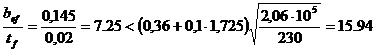 .
.
Определяем фактические характеристики скомпонованного сечения:
Фактическая площадь сечения:
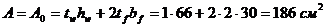 .
.
Моменты инерции:
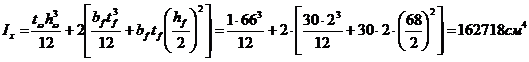
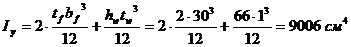 .
.
Радиусы инерции:
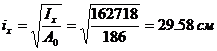 ;
;
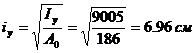 .
.
Момент сопротивления:
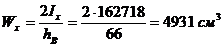 .
.
Ядровое расстояние:
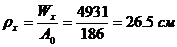 .
.
Проверяем устойчивость верхней части колонны в плоскости рамы:
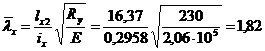 ;
;
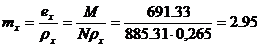 .
.
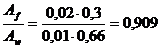 .
.
По приложению СНиП:
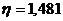 .
.
Приведенный относительный эксцентриситет:
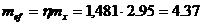 .
.
По табл. СНиП 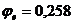 .
.
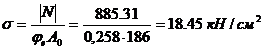 .
.
Оцениваем недонапряжение:
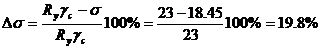 ;
;
Проверяем устойчивость верхней части колонны из плоскости рамы:
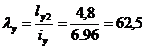 Þ
Þ 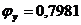 .
.
Найдем максимальный момент в средней трети расчетной длины стержня:
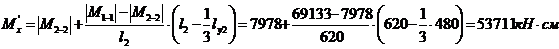 ,где
,где
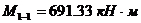 – расчетный момент, по которому проектируется колонна;
– расчетный момент, по которому проектируется колонна;
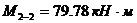 – соответствующий момент в сечении 2-2 при тех же номерах нагрузок, что и М1-1.
– соответствующий момент в сечении 2-2 при тех же номерах нагрузок, что и М1-1.
Относительный эксцентриситет:
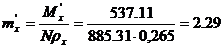 .
.
Определяем коэффициент c, учитывающий влияние изгибающего момента на устойчивость из плоскости его действия, т.к. mx£5:
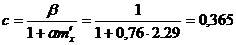 .
.
где 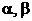 - коэффициенты, определяемые по таблице 10 [4]:
- коэффициенты, определяемые по таблице 10 [4]:
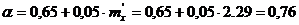 ;
;
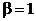 , т.к.
, т.к. 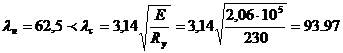 ;
;
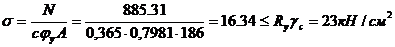 .
.
Устойчивость из плоскости рамы обеспечена.
При изгибе колонн относительно оси y материал стенки работает в упругой стадии, поэтому устойчивость стенки проверяем по упругим формулам.
Наибольшее сжимающее напряжение в стенке:
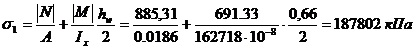 .
.
Соответствующее напряжение у противоположного края стенки:
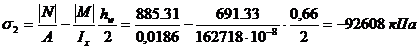 .
.
Среднее касательное напряжение в стенке:
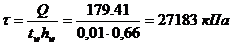 , где
, где
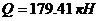 – поперечная сила в сечении 1-1 при тех же номерах нагрузок, что М и N.
– поперечная сила в сечении 1-1 при тех же номерах нагрузок, что М и N.
Определяем коэффициенты:
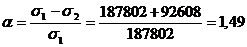 ;
;
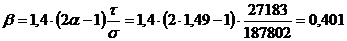 .
.
При 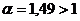
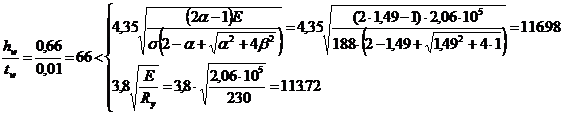 .
.
Устойчивость стенки обеспечена.
Т.к. 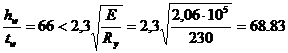 , то укреплять стенку поперечными ребрами жесткости нет необходимости.
, то укреплять стенку поперечными ребрами жесткости нет необходимости.
