Методика статистической обработки результатов экспериментов

Натуральные

Переход из нормализованных обозначений факторов (Х1.Х2.....Xn) в натуральные производят по следующим формулам (для членов модели типа Аi*Xi)

A_i*(X_i -X_i⁽⁰⁾)/d , (26)

где A_i - числовое значение коэффициента при соответствую­щем переменном факторе X₁, Х₂.....Хn;

X_i - буквенное обозначение переменного фактора, приня­тое в системе обозначений;

X_i⁽⁰⁾ - численное значение переменного фактора, соот­ветствующее нулевому уровню интервала варьирова­ния;

d – шаг варьирования, равный разности значений ин­тервала, соответствующего нулевому и нижнему уровням варьирования факторов;

(для членов модели типа A_iiX_i²)

A_ii*(X_i-X_i⁽⁰⁾)²/d , (27)

где A_ii - числовое значение коэффициента при соответствую­щем квадратичном переменном факторе Х₁,Х₂...Х_n;

X_i - буквенное обозначение переменного фактора приня­тое в системе обозначений;

X_i⁽⁰⁾- численное значение переменного фактора, соот­ветствующее нулему уровню интервала варьирова­ния;

d - шаг варьирования, равный разности значений интервала, соответствующего нулевому и нижнему уровням варьирования факторов;

(для членов модели типа A_ijX_iX_j)

A_ij ((X_i –X_i⁽⁰⁾)*( X_j- X_j⁽⁰⁾))/(d₁*d₂) (28)

где A_ij - числовое значение коэффициента при соответствующем парном взаимодействии факторов;

X_i - буквенное обозначение переменного фактора приня­тое в системе обозначений;

X_i⁽⁰⁾ - численное значение переменного фактора, соот­ветствующее нулевому уровню интервала варьирования;

X_j⁽⁰⁾ - численные значения второго переменного фактора парного взаимодействия, соответствующее нулевому уровню интервала варьирования;

d₁, d₂ - шаг варьирования первого и второго факторов парного взаимодействия, равный разности значений интервала, соответствующего нулевому и нижнему уровням варьирования факторов.

После преобразований членов модели в соответствии с форму­лами в полученном уравнении приводятся подобные члены, т.е. свободные члены группируется со свободными, квадра­тичные эффекты переменных факторов с квадратичными эффектами и т. д. В результате получается модель в натуральных обозначениях факторов. Следует отметить необходимость учета знаков при коэф­фициентах и свободного члена при группировании членов математи­ческой модели.

7 Анализ математической модели функционирования объекта

исследования

Это заключительный этап планирования эксперимента, на ко­тором исследователь, пользуясь математической моделью, получает необходимую информацию об объекте исследования.

В этой части работы должно быть проведено сопоставление и обобщение всего комплекса полученных данных, а затем оценка ре­зультатов проведенной работы. При анализе производится раскры­тие причинного характера взаимодействия между отдельными факто­рами, по возможности устанавливается и объясняется физическая сущность изучаемого явления.

Анализ модели лучше всего проводить, пользуясь уравнением регрессии в нормализованных обозначениях факторов. Анализ моде­ли производится на доминирующее влияние факторов на исследуемую величину. Для этого по каждому фактору берут частные производ­ные и суммируют значения коэффициентов по модулю. Тот фактор, у которого эта сумма получилась наибольшей, оказывает большее влияние на объект исследования.

Важную информацию несут знаки коэффициентов регрессии. Ес­ли линейные коэффициенты уравнения положительны, то выходная величина возрастает с увеличением соответствующего фактора и наоборот.

Уравнение регрессии позволяет предсказать значение выход­ной величины для любой точки внутри области варьирования факто­ров.

По моделям второго порядка проводится оптимизация процес­сов деревообработки в соответствии с методикой исследования регрессионных моделей для решения задач оптимизации.

По модели, в натуральных обозначениях, строят графики за­висимости выходной величины от фактора при закрепленных значе­ниях остальных факторов.

Можно строить графики зависимости выходной величины от нескольких факторов при закреплении значений одного из факто­ров. При этом допускается совмещать оси и значения уровней пе­ременных факторов.

Древесины

Пояснительная записка к курсовой работе

по дисциплине:

“НАУЧНЫЕ ИССЛЕДОВАНИЯ В ДЕРЕВООБРАБОТКЕ”

КР ТД 081 ПЗ

Разработал И.В.Сипилин

Студент группы ТД-302 № зачётной книжки 06-3.081

Специальность (260200 «Технология деревообработки»)

Руководитель работы

Канд. техн. наук, доцент ________________________________ Г.В. Глотов

Члены комиссии

Канд. тех. наук, доцент _________________________________ Г.В. Глотов

Канд. тех. наук, доцент _________________________________ А.А Лукаш

Брянск 2008

Методика статистической обработки результатов экспериментов

После проведенных опытов необходимо провести статистическую обработку результатов эксперимента по следующей методике:

- рассчитать построчные средние значения по каждому опыту;

- рассчитать построчные дисперсии по каждому опыту;

- рассчитать построчные средние квадратические отклонения по каждому

опыту.

Построчные средние значения Уср. результатов опытов расс­читываются по

формуле

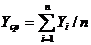, (1)

где Y_i - i-ое значение опыта;

n - Число повторений опыта.

Построчные дисперсии S² рассчитываются по формуле

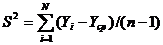. (2)

Построчные средние квадратические отклонения S рассчиты­ваются по

формуле

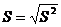. (3)

Рассчитав статистические показатели, производят оценку значений выходной величины на грубую ошибку. Грубым считается тот результат, который по-своему численному значению сильно отличается от других значений выходной величины. Если экспериментатор подозревает результат замера выходной величины, как грубый замер, то подтвердить или отвергнуть данное предположение можно при помощи расчетного критерия Стьюдента (tp) по формуле

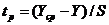, (4)

где Yср - построчное среднее значение по опытам;

Y - Подозреваемый на грубую ошибку результат;

S - Среднее квадратическое отклонение выборки;

По таблицам определяют табличное значение критерия Стьюдента (tт), которое зависит от уровня значимости (q=0, 05è40) и числа степеней свободы (f=n-l).

/ 1, с. 223 /

Если tт >tp, то подозреваемый на грубую ошибку результат не является

грубым. Если же условие не выполняется, то результат считается грубой ошибкой и

исключается из выборки замеров выходной величины, а эксперимент для опыта, где находился грубый результат повторяется.

После расчета статистических показателей по каждому опыту, проводят регрессионный анализ, т.е. рассчитывают коэффициенты математической модели.

5 Методика регрессионной обработки результатов экспери­ментов

Как отмечалось выше, по эксперименту можно получать модели в виде полинома первого и второго порядков. Следует отметить, что порядок получения моделей первого и второго порядков в целом не отличается, однако при расчете коэффициентов и проверки адекватности модели есть некоторые различия.

5.1 Методика получения математической модели по униформ-ротатабельному

плану

Математическая модель, получаемая по униформ-ротатабельному плану, это модель второго порядка, которая для трех переменных факторов имеет вид

У=А₀+А₁*Х₁+А*Х₂+А₃*Х₃+А₁₁*Х₁²+А₂₂*Х₂²+А₃₃*Х₃²+

+А₁₂*Х₁*Х₂+ А₁₃*Х₁*Х₃+ А₂₃*Х₂*Х₃ , (5)

где Ао - свободный член уравнения регрессии (модели);

А₁ - коэффициент при переменном факторе X₁:

А₂ - коэффициент при переменной факторе Х₂;

А₃ - коэффициент при переменной факторе Х₃;

А₁₂ - коэффициент при парном взаимодействии факторов X₁ и Х₂;

А₁₃ - коэффициент при парном взаимодействии факторов X₁ и Х₃;

А₂₃ - коэффициент при парном взаимодействии факторов X₂ и Х₃;

А₁₁ - коэффициент при квадратичном эффекте фактора X₁;

А₂₂ - коэффициент при квадратичном эффекте фактора Х₂;

А₃₃ - коэффициент при квадратичном эффекте фактора Х₃;

Однородность дисперсий проверяется по формуле

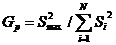, (6)

где 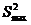-максимальное значение дисперсии;

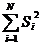- суммарное значение дисперсии.

Затем определяются коэффициенты модели А₀,А_1,А₂,А₃, А₁₁, А₂₂, А₃₃, А₁₂, А₁₃, А₂₃ по формулам

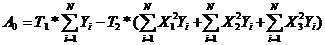, (7)

где 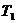, 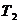- коэффициенты, выбираемые по таблице;

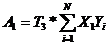; (8)

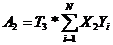; (9)

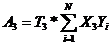; (10)

где 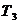- коэффициент, выбираемый по таблице для количества факторов К=3

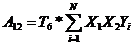; (11)

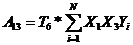; (12)

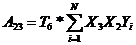; (13)

где Т₆ - коэффициент, выбираемый по таблице для количества факторов К=3

/ 1, с. 121 /

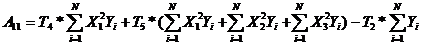; (14)

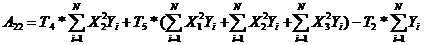; (15)

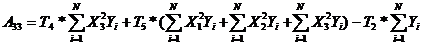; (16)

где 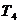, 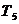- коэффициент, выбираемый по таблице для количества факторов К=3. / 1, с. 121 /

После расчета коэффициентов модели их проверяют на значи­мость по формулам

t_p{A_i}= 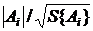, (17)

где t_p{A_i} - расчетное значение критерия Стьюдента;

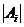- значение коэффициента при соответству­ющем факторе по абсолютной величине;

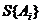- среднее квадратическое отклонение коэффи­циента;

t_p{A_ij}= 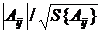, (18)

где t_p{A_ij} - расчетное значение критерия Стьюдента;

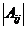- значение соответствующего коэффициента при парном взаимодействии факторов по абсолютной величине;

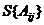- среднее квадратическое отклонение коэффи­циента.

t_p{A_ii}= 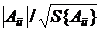, яя (19)

где t_p{A_ii} - расчетное значение критерия Стьюдента;

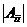- значение соответствующего коэффициента при квадратичном факторе по абсолютной величине;

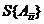- среднее квадратическое отклонение коэффи­циента.

Дисперсии коэффициентов регрессии определяются по формулам

S²{A_i}=(T₃/n)*S²{A_ср}, (20)

где S²{A_i} - дисперсия коэффициента при соответствующем факторе;

Т₃ - табличный коэффициент;

S²{A_ср} - дисперсия среднего, характеризующая ошибку среднего;

n – число повторений опыта.

S²{A_ii}=((T₄+T₅)/n)*S²{A_ср}, (21)

где S²{A_ii} - дисперсия коэффициента при соответствующем квадра-

тичном факторе;

T₄,T₅ - табличные коэффициенты;

S²{A_ср} - дисперсия среднего, характеризующая ошибку среднего;

n - число повторений опыта.

S²{A_ij}=(T₆/n)*S²{A_ср}, (22)

где S²{A_ij} - дисперсия коэффициента при парном взаимодей­ствии

факторов;

T₆- табличный коэффициент;

S²{A_ср} - дисперсия среднего, характеризующая ошибка среднего;

n - число повторений опыта.

Дисперсия среднего S²{A_ср} рассчитывается по формуле

S²{A_ср}= 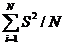, (23)

где 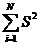- суммарное значение дисперсии;

N - число опытов.

Затем по таблицам в зависимости от уровня значимости (q=0,05) и числа степеней свободы, рассчитываемого по формуле

f =N*(n-1), (24)

ус­танавливают табличный критерий Стьюдента(t_p) и сравнивают его с расчетным. Коэффициент считается значимым если t_p>t_т . Если это условие не выполняется, то коэффициент вместе с соответс­твующим ему фактором исключается из модели.

/ 1, с. 223 /

После проверки значимости коэффициентов, модель проверяют на адекватность.

Если модель после проверки на значимость коэффициен­тов не претерпела

изменений ее переписывают, заменяя буквенные обозначения коэффициентов

(А₀,А_1,А₂,А₃, А₁₁, А₂₂, А₃₃, А₁₂, А₁₃, А₂₃), на их числен­ные значения, полученные по формулам.

Адекватность модели проверяется по расчетному критерию Фишера (Fp), который определяется по формулам

Fp= 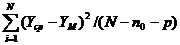, (25)

где 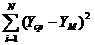- сумма квадрата разности между средним значением опыта и полученным по уравнению;

N - число опытов;

n₀ – число опытов в центре плана;

р - число значимых коэффициентов модели;

По таблицам в зависимости от уровня значимости (q=0,05), числа степеней свободы f₁ = N – n₀ - р и числа степеней свободы f₂ = N*(n - 1), выбирают табличный критерий Фишера F_т. Если Fp < F_т, то полученная математическая модель адекватно описывает объект исследования. Если условие не выполняется, принимается одно из следующих решений: / 1, с. 224 /

-переходят к плану другого порядка;

-уменьшают диапазон варьирования факторов.

6 Методика перехода из нормализованных обозначений фак­торов в

Натуральные

Переход из нормализованных обозначений факторов (Х1.Х2.....Xn) в натуральные производят по следующим формулам (для членов модели типа Аi*Xi)

A_i*(X_i -X_i⁽⁰⁾)/d , (26)

где A_i - числовое значение коэффициента при соответствую­щем переменном факторе X₁, Х₂.....Хn;

X_i - буквенное обозначение переменного фактора, приня­тое в системе обозначений;

X_i⁽⁰⁾ - численное значение переменного фактора, соот­ветствующее нулевому уровню интервала варьирова­ния;

d – шаг варьирования, равный разности значений ин­тервала, соответствующего нулевому и нижнему уровням варьирования факторов;

(для членов модели типа A_iiX_i²)

A_ii*(X_i-X_i⁽⁰⁾)²/d , (27)

где A_ii - числовое значение коэффициента при соответствую­щем квадратичном переменном факторе Х₁,Х₂...Х_n;

X_i - буквенное обозначение переменного фактора приня­тое в системе обозначений;

X_i⁽⁰⁾- численное значение переменного фактора, соот­ветствующее нулему уровню интервала варьирова­ния;

d - шаг варьирования, равный разности значений интервала, соответствующего нулевому и нижнему уровням варьирования факторов;

(для членов модели типа A_ijX_iX_j)

A_ij ((X_i –X_i⁽⁰⁾)*( X_j- X_j⁽⁰⁾))/(d₁*d₂) (28)

где A_ij - числовое значение коэффициента при соответствующем парном взаимодействии факторов;

X_i - буквенное обозначение переменного фактора приня­тое в системе обозначений;

X_i⁽⁰⁾ - численное значение переменного фактора, соот­ветствующее нулевому уровню интервала варьирования;

X_j⁽⁰⁾ - численные значения второго переменного фактора парного взаимодействия, соответствующее нулевому уровню интервала варьирования;

d₁, d₂ - шаг варьирования первого и второго факторов парного взаимодействия, равный разности значений интервала, соответствующего нулевому и нижнему уровням варьирования факторов.

После преобразований членов модели в соответствии с форму­лами в полученном уравнении приводятся подобные члены, т.е. свободные члены группируется со свободными, квадра­тичные эффекты переменных факторов с квадратичными эффектами и т. д. В результате получается модель в натуральных обозначениях факторов. Следует отметить необходимость учета знаков при коэф­фициентах и свободного члена при группировании членов математи­ческой модели.

7 Анализ математической модели функционирования объекта

исследования

Это заключительный этап планирования эксперимента, на ко­тором исследователь, пользуясь математической моделью, получает необходимую информацию об объекте исследования.

В этой части работы должно быть проведено сопоставление и обобщение всего комплекса полученных данных, а затем оценка ре­зультатов проведенной работы. При анализе производится раскры­тие причинного характера взаимодействия между отдельными факто­рами, по возможности устанавливается и объясняется физическая сущность изучаемого явления.

Анализ модели лучше всего проводить, пользуясь уравнением регрессии в нормализованных обозначениях факторов. Анализ моде­ли производится на доминирующее влияние факторов на исследуемую величину. Для этого по каждому фактору берут частные производ­ные и суммируют значения коэффициентов по модулю. Тот фактор, у которого эта сумма получилась наибольшей, оказывает большее влияние на объект исследования.

Важную информацию несут знаки коэффициентов регрессии. Ес­ли линейные коэффициенты уравнения положительны, то выходная величина возрастает с увеличением соответствующего фактора и наоборот.

Уравнение регрессии позволяет предсказать значение выход­ной величины для любой точки внутри области варьирования факто­ров.

По моделям второго порядка проводится оптимизация процес­сов деревообработки в соответствии с методикой исследования регрессионных моделей для решения задач оптимизации.

По модели, в натуральных обозначениях, строят графики за­висимости выходной величины от фактора при закрепленных значе­ниях остальных факторов.

Можно строить графики зависимости выходной величины от нескольких факторов при закреплении значений одного из факто­ров. При этом допускается совмещать оси и значения уровней пе­ременных факторов.