Приток жидкости к добывающей скважине, производительность совершенной и несовершенной скважины и методы оценки ПЗС

Приток жидкости в скважины происходит под действием разницы между пластовым давлением и давлением на забое скважины. Разность между пластовым и забойным давлением называется депрессией на пласт.

ΔР = Рпл – Рзаб

(1.20)

Так как движение жидкости в пласте происходит с весьма малыми скоростями, то оно подчиняется линейному закону фильтрации - закону Дарси. При постоянной толщине пла­ста и открытом забое скважины жидкость движется к забою по радиально-сходящимся направлениям. В таком случае говорят о плоскорадиальной форме потока. Если скважина достаточно продолжительно работает при постоянном забойном давлении, то скорость фильтрации и давление во всех точках пласта перестают изменяться во времени и поток является установившимся.

Рассмотрим задачу притока жидкости в скважину в круго­вом пласте, схема которого представлена на рис. 1.5.

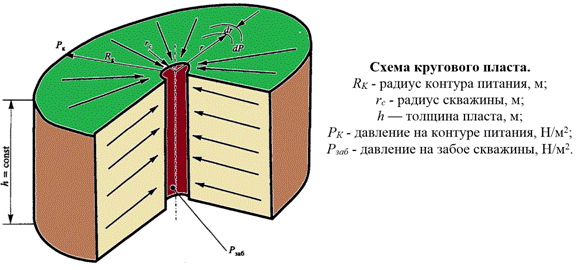
Рис. 1.5. Схема плоско-радиального притока пластовой жидкости в добывающую скважину из кругового пласта

Рассмотрим задачу плоско-радиального притока жидкости в скважину в круговом пласте.

Для решения задачи введем следующие допущения:

1. Пласт круговой, в центре которого расположена единственная совершенная скважина.

2. Пласт однородный и изотропный постоянной толщины.

3. Процесс течения флюида изотермический (μ = const).

4. Движение жидкости плоско-радиальное и соответствует закону Дарси.

5. В процессе фильтрации отсутствуют любые физические и химические реакции.

Запишем уравнение Дарси:

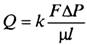(1.21)

где, Q – объемный расход жидкости, м³/с;

F – поверхность фильтрации, м²;

ΔР – перепад давлений, Па;

μ – вязкость флюида, Па с;

l – путь течения флюида, м;

k – коэффициент пропорциональности, который учитывает не только среду в которой осуществляется фильтрация, но и все процессы взаимодействия между фильтрующимся флюидом и твердой поверхностью среды, м².

Для схемы рис. 1.5 обозначим:

R_k — радиус контура питания (равен половине расстояния между двумя соседними скважинами), м;

r_с— радиус скважины, м;

h — толщина пласта, м;

Р_к — давление на контуре питания, Па;

Р_заб — давление на забое скважины, Па.

Выделим на расстоянии r от оси скважины элемент пласта толщиной dr. Перепад давлений на этом элементе обозначим через dP. Поверхность фильтрации для выделенного элемента такова:

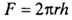(1.22)

Запишем уравнение Дарси для рассматриваемой схемы:

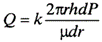(1.23)

Пределами интегрирования для являются:

· по Р: от Р_к до Р_заб;

· по r: от R_к до r_c.

Таким образом, имеем уравнение Дюпюи и описывающее приток жидкости в совершенную скважину для рассмотренной схемы (см. рис.1.5) при принятых выше допущениях:

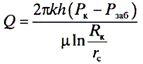(1.24)

где Р_к = Р_пл, Р_заб = Р_с, R_к = R = R_др.

Режимы течения жидкости к скважине из пласта

Радиальный режим течения – наиболее значимый режим с точки зрения интерпретации данных ГДИС. При радиальном режиме течения линии тока направлены к круговому цилиндру радиусом r (рис. 1.6 А).

Для скважины, вскрывающей пласт на всю продуктивную толщину, радиус цилиндра равен радиусу скважины r_с. Для скважины, вскрывающей только часть продуктивной толщины, радиальный приток относится только к начальному периоду исследования и только для той части пласта, в которой линии тока направлены горизонтально к скважине (рис. 1.6 Б).

Для скважин с ГРП и горизонтальных скважин эффективный радиус для радиального притока значительно больше чем r_с. Приток к горизонтальной скважине в начальный период теста также является радиальным в вертикальной плоскости, перпендикулярной к стволу скважины (рис. 1.6 В, Г).

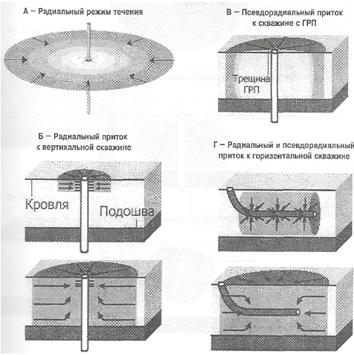
Рис. 1.6. Радиальный режим течения

Сферический режим течения – линии тока сходятся в одной точке (рис. 1.7 А).

Сферический или полусферический режим притока случается в скважинах, несовершенных по степени вскрытия:

· частичное вскрытие (рис. 1.7 В);

· частичное проникновение (рис. 1.7 Б).

Линейный режим течения - линии тока строго параллельны (рис. 1.8).

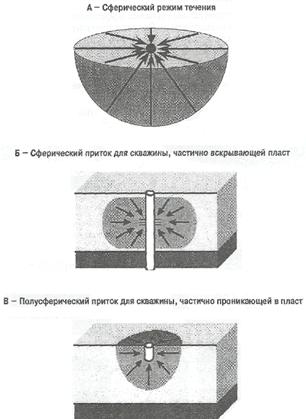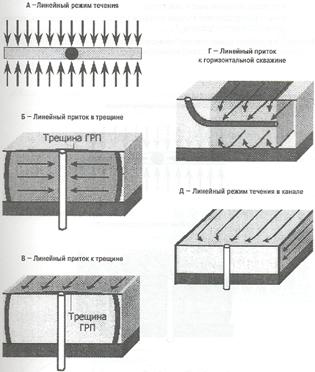Рис. 1.7. Сферический режим течения

Рис. 1.8. Линейный режим течения

Скважины с трещиной ГРП могут иногда выходить на билинейный режим течения дополнительно к линейному режиму притока или вместо него (рис. 1.9 А).

Билинейный режим притока возникает в результате того, что:

· из-за перепада давления в самой трещине возникают параллельные линии тока в трещине, направленные к скважине;

· из-за перепада давления в пласте возникают параллельные линии тока, направленные из пласта к трещине.

Термин "билинейный режим течения" относится к случаю, когда существует одновременно два взаимно-перпендикулярных линейных притока (рис. 1.9 Б).

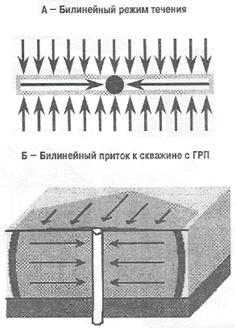
Рис. 1.9. Билинейный режим течения

Производительность фактической скважины

Производительность скважины описывается законом Дарси. Закон Дарси не является теорией или предположением, это – ЗАКОН!

Производительность (дебит) реальной скважины с учетом скин-эффекта по закону Дарси и формуле Дюпюи можно записать в виде:

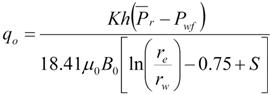(1.25)

где, q_о – объемный дебит нефти, м³/сут;

K – проницаемость пласта (эффективная проницаемость нефти), мД;

h – эффективная мощность пласта (м);

P_r = Р_к = Р_пл – среднее пластовое давление (атм);

P_wf = Р_с = Р_заб – забойное давление в скважине, атм;

m_о – вязкость нефти, сПз (в пластовых условиях);

B_о – объемный коэффициент нефти, м³/м³;

r_е = R = R_к – радиус дренирования, м;

r_w = r_c – радиус скважины, м;

S – скин-эффект, д.ед;

18.41 – пересчетный коэффициент.

Пересчетный коэффициент можно вычислить: 1/18.41 = 0.054318305

С другой стороны:

1/18.41 = 2*p{3.141593}*10^-3{перевод проницаемости из мкм² в мД}/10³{перевод вязкости из Па*с в мПа*с}*10^-1{перевод давления из МПа в атм}*86400 {перевод времени из сек в сут}= 0.054286721

Кроме того, можно учесть, что 1 атм = 101325 Па (а не 10⁵) и 1 Д = 1,02 мкм²
(а не 1 мкм²).

Закон Дарси является одним из самых главных уравнений в разработке месторождений.

Режимы притока пластовой жидкости в добывающую скважину

Установившийся – распределение давления и дебита постоянно во времени. Данный тип притока возможен только при поддержке постоянного давления на границе пласта, т.е. при наличии большой газовой шапки, активной законтурной области или в случае проведения мероприятий по поддержанию пластового давления:

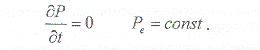
Неустановившийся – давление и/или дебит изменяются во времени, т.е. случай, когда перераспределение давления еще не достигло границ пласта и/или пока не проявляется влияние соседних скважин:

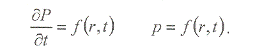
Псевдоустановившийся – профиль давления постоянен во времени. Давление на границе снижается. Данный режим притока характерен для изолированных пластов с непроницаемыми границами (рис. 1.8.2):

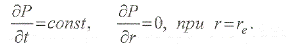
ГДИС почти всегда выполняются на неустановившемся режиме притока, даже если и начинает проявляться влияние границ пласта.

Графически проявление этих режимов при притоке жидкости в добывающую скважину во времени показано на рис. 1.10.

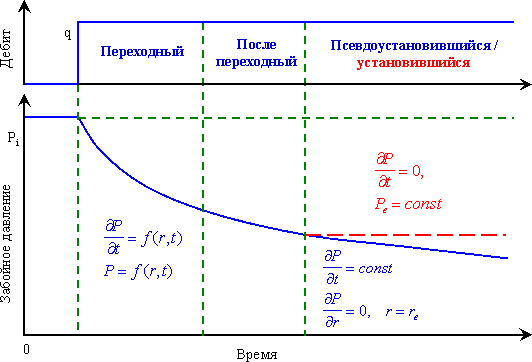
Рис. 1.10. Проявление режимов притока пластовой жидкости в добывающую скважину

Таким образом производительность (дебит) реальной скважины с учетом скин-эффекта по закону Дарси и формуле Дюпюи согласно (1.25), можно записать для каждого типа режимов притока пластовой жидкости в добывающую скважину.

Неустановившийся режим притока:

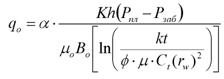
Псевдоустановившийся режим притока:

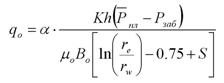
Установившийся режим притока:

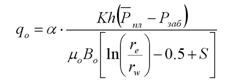
где, α – пересчетный коэффициент, который зависит от используемых единиц. Значения представлены в таблице 1.1.

Таблица 1.1. Значения пересчетного коэффициента α

Система	СИ	Российские промысловые	Американские промысловые
Дебит	м3/сек	м3/сут	bbl/day
Время	секунда	сутки	day
Давление	Паскаль (Па)	Атмосфера (атм)	psi
Проницаемость	м2	мД	mD
Вязкость	Па·сек	сПз	cP
Объемный коэффициент	м3/м3	м3/м3	bbl/stb
Коэффициент (α)	2π	1/18,41	1/141,2

Распределение давления в пласте

Распределение давления в пласте вокруг работающей скважины является логарифмическим, что представлено на рис. 1.11.

Давление на контуре питания Р_к является пластовым статическим давлением Р_пл.ст , в дальнейшем просто Р_пл (Р_пл.ст - статическое пластовое давление - давление, которое существует в системе до момента отбора продукции, т.е. когда Q = 0). Давление вокруг работающей скважины в любой точке пласта (между давлением на забое скважины и давлением на контуре питания) называется динамическим пластовым давлением Р. Динамическое пластовое давление на стенке скважины будем называть забойным давлением Р_заб.

Разность между статическим и динамическим пластовыми давлениями называется депрессией ΔР:

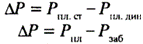
Если линию распределения давления повернуть вокруг оси скважины, получится так называемая воронку депрессии. Депрессия (потери энергии при движении продукции от контура питания до стенки скважины) существенно возрастает на определенном расстоянии от стенки скважины.

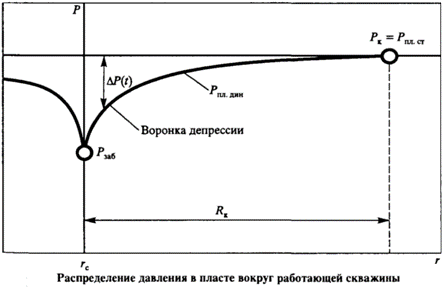
Рис. 1.11. Распределение давления в пласте вокруг работающей скважины

Под призабойной зоной скважины будем понимать зону, прилегающую к стенкам скважины, в которой существенно возрастают фильтрационные сопротивления движению продукции. До настоящего времени не существует никаких рекомендаций по численному определению радиуса этой зоны, что в значительной степени осложняет оценку эффективности различных методов искусственного воздействия на призабойные зоны скважин и сравнение их между собой.

Рассмотрим некоторые возможности численной оценки размеров ПЗС.

Первая возможность (рис. 1.12) базируется на аппроксимации ветвей логарифмической зависимости Р = f(r) прямыми линиями 1 и 2, которые пересекаются в точке А. Эта точка и дает размеры (радиус) призабойной зоны скважины – r_пзс. Данный прием не является единственно возможным.

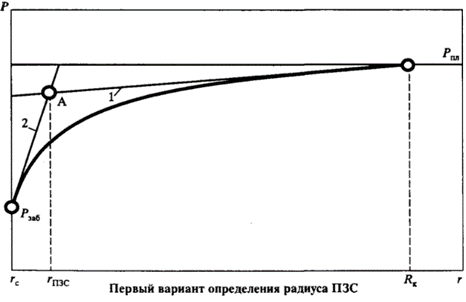
Рис. 1.12. Метод оценки ПЗС путем аппроксимации ветвей логарифмической зависимости Р = f(r)

Численная оценка размеров призабойной зоны может быть определена и по-другому (рис. 1.13).

Например, можно разбить суммарные потери энергии при движении продукции от контура питания до стенки скважины поровну, т.е. чтобы площади S₁ и S₂ были равны. Граница этих площадей и будет численно определять радиус ПЗС. Совершенно очевидно, что для оценки размеровПЗС можно предложить и другие методы.

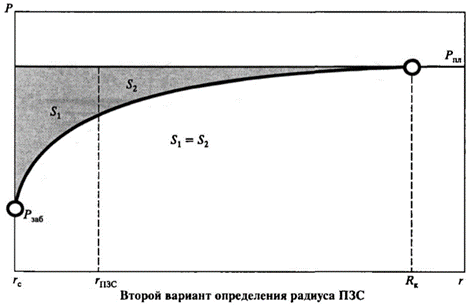
Рис. 1.13. Метод оценки ПЗС путем разделения суммарных потерь энергии при движении продукции от контура питания до стенки скважины поровну

Важно: какой бы метод оценки размеров ПЗС не использовался, если возникает необходимость сравнения результатов, зависящих от размеров ПЗС, при этом сравнении необходимо в обоих случаях использовать один и тот же метод расчета размеров (радиуса) ПЗС.