Стратегии развития критического мышления при обучении в школе
Введение
Ведущей характеристикой образования сегодня является ее нацеленность на обработку большого количества информации, развитость коммуникативных навыков и готовность личности к переменам.
В этих условиях формирование системы качественного образования граждан представляет собой стратегическую задачу, ввиду того, что конкурентоспособность государства зависит от уровня образованности и развитости каждого. Как показывает опыт стран с высоким уровнем развития системы образования, например, Финляндии, Японии, Сингапура (сегодня в этот список входит и Китай), это быстро сказывается на развитии науки, технологий, следовательно, и на развитии экономики и уровня жизни в этих странах. Одновременно образованность граждан стабилизирует социальную обстановку в обществе, ведь уверенность в будущем базируется на уверенности в том, что человек всегда найдет работу.
Сегодня Казахстан идет по пути реформирования системы образования на всех ее уровнях и становления своей уникальной модели. Одним из принципиальных требований к результатам образования школьников является их способность применять на практике полученные в школе знания, умения и навыки. Одним из отправных моментов для преобразования математической подготовки школьников являются результаты международного тестирования школьников по системе PISA и TIMSS. Эти исследования показывают способность школьников применять знания по математике в повседневной жизни (PISA) и уровень математических знаний (TIMSS). Результаты исследований показали, что наши школьники не владеют умением представления задач, возникающих в повседневности, в виде математической задачи, следовательно, не могут продемонстрировать знания приемов их решения.
Задачи обучения математики в школе не изменились в связи с изменением подходов к формированию математических знаний школьников. Л.Д.Кудрявцев, автор учебников по алгебре и началам анализа, пишет: «Целью при обучении математике является приобретение учащимися определенного круга знаний, умений использовать изученные математические методы, развитие математической интуиции, воспитание математической культуры. ...Для правильной постановки задачи, для оценки ее данных, для выделения существенных из них и для выбора способа ее решения необходимо обладать еще математической интуицией, фантазией и чувством гармонии, позволяющим предвидеть нужный результат, прежде чем он будет получен. В результате приобретенных в процессе обучения математике знаний и интуиции у учащихся появляется то, что обычно называется математической культурой" .
Характеристиками критического мышления являются, как известно, его самостоятельность, умение поставить проблему. Последнее подразумевает сбор информации о том, что известно, что нужно узнать и какие есть для этого средства, а также умения определить чего недостает для решения этой проблемы. На этой основе нужно уметь выбрать оптимальный метод ее решения. Это решение должно быть четко аргументировано. Таким образом, ученик должен уметь защитить свое решение в процессе общения со сверстниками, учителем, экзаменатором. Обладание такими умениями, очевидно, как нельзя лучше формируется в результате обучения математике, ввиду совпадения целей обучения математике с задачами формирования критического мышления школьников.
Актуальность темы исследования «Применение стратегий развития критического мышления при обучении тригонометрическим функциям в школе» обосновывается тем, что сегодня проблема достижения целей обучения математике в школе заключается не в столько в содержании обучения математике, сколько в средствах достижения этой цели. На сегодняшний день развитие критического мышления школьников является одним из эффективных средств, призванных добиться реализации целей обучения математике в школе.
Целью дипломного исследования является реализация стратегии развития критического мышления школьников в процессе обучения тригонометрическим функциям в школе
Объект исследования: процесс обучения тригонометрическим функциям в школе. Предмет исследования: реализация стратегий критического мышления в процессе обучения тригонометрическим функциям в школе.
Задачи исследования:
1. на основе анализа психолого- педагогической литературы раскрыть суть технологии критического мышления;
2. на основе анализа методической литературы раскрыть методику обучения тригонометрическим функциям в школе.
3. На основе изученной методики разработать примеры применения стратегий развития критического мышления школьников на уроках математики при изучении темы: «Тригонометрические функции»
Методы исследования:
- теоретический анализ психолого-педагогической литературы;
- анализ методической литературы по изучению тригонометрических функций в школе;
- педагогические наблюдения;
- беседы;
- изучения педагогической документации и работ учеников;
- анализ результатов учебной деятельности учеников.
Теоретической основой исследования явились труды отечественных и зарубежных педагогов, психологов и методистовОмарова В.К.,Мынбаева А.К., Загашев И.О.
Прием «Шесть шляп мышления»
В практику развития мышления метафору «шести шляп» ввел известный психолог Эдвард де Боно. Выражение «putonyourthinkinghat (cap)» (дословно: надень свою мыслительную шляпу) на русский язык можно перевести как «призадуматься, поразмыслить». Обыгрывая этот оборот, Э. де Боно предлагает «поразмыслить» шестью различными способами.
8.«Синквейн».Эта пятистрочнаястихотворная форма, возникшая в США в начале XX века под влиянием японскойпоэзии. В дальнейшем стала использоваться (в последнее время, с 1997 года, и в России) в дидактических целях, как эффективный метод развития образной речи, который позволяет быстро получить результат. Синквейны в учебно-воспитательном процессе полезны в качестве инструмента для синтезирования сложной информации, в качестве среза оценки понятийного и словарного багажа учащихся.
Порядок написания синквейна: Первая строка – одно ключевое слово, определяющее содержание синквейна.
Вторая строка – два прилагательных, характеризующих данное предложение.
Третья срока – три глагола, показывающие действие понятия.
Четвёртая строка – короткое предложение, в котором автор высказывает своё отношение.
Пятая строка – одно слово, обычно существительное, через которое человек выражает свои чувства, ассоциации связанные с данным понятием. Тем для синквейна великое множество. Возьмем для примера историю России ХХ века: война, революция, Государственная дума, реформа Столыпина, Ленин, Ленд-лиз, "холодная война", НАТО, культ личности, "застой" и т.д.
9. Эссе – один из приёмов, который используют в технологии развития критического мышления. Целесообразно использовать как небольшое письменное задание, обычно, на стадии рефлексии. Суть этого метода не только в том, чтобы выразить свои мысли в письменной форме, но и поделиться своим мнением с другими, выслушать чужую точку зрения. Детям (да и не только им) не всегда легко выразить свое мнение в развернутом, логичном виде сразу, – читая свои записи это сделать проще. Ни в коем случае нельзя оценивать эти эссе с точки зрения грамотности. Их нужно воспринимать как способ развития мышления и формирование культуры чтения. Различают 5-минутное эссе, 10-минутное эссе, а также более продолжительные и трудоемкие сочинения.
10-минутное эссе. После чтения (прослушивания) и общего обсуждения текста учащимся предлагается организовать свои мысли с помощью 10-минутного эссе (по методике свободного письма). Для этого учитель просит, в течение 10 мнут писать на предложенную тему. Главное правило свободного письма – не останавливаться, не перечитывать, не исправлять. При затруднении можно письменно прокомментировать возникшую проблему и постараться писать дальше. Иногда текст свободного эссе предлагается использовать как подготовительный этап работы для более солидного сочинения.
5-минутное эссе. Этот вид письменного задания обычно применяется в конце занятия, чтобы помочь учащимся подытожить свои знания по изученной теме. Для учителя – это возможность получить обратную связь. Поэтому учащимся можно предложить два пункта: 1) написать, что они узнали по новой теме; 2) задать один вопрос, на который они так и не получили ответа. Очень интересными получились работы учащихся на темы «Банки охотно дают деньги тем, кто может доказать, что в них не нуждается»«Богатым человека делает его сердце»Л. Толстой, «События октября 1917 года – это социалистическая революция или государственный переворот?» и т.д. Очень актуальной стала эта форма в связи с новой системой итоговой аттестации. Одно из заданий ЕНТ необходимо выполнить в виде небольшой письменной работы – эссе.
Ход урока
Вводно-мотивационная часть
1.1.Организационный момент.
Задачи этапа: обеспечить внешнюю обстановку для работы на уроке, психологически настроить учащихся к общению.
Содержание этапа:
1. Приветствие.
Учитель: Здравствуйте, садитесь! Запишите сегодняшнее число и тему урока. “Метод замены для решения некоторых тригонометрических уравнений”. Задания по решению тригонометрических уравнений встречаются в вариантах ЕНТ.
2. Проверка готовности учащихся к уроку.
Учитель: Ребята, кто сегодня отсутствует? Все готовы к уроку? Итак, внимание. Начинаем!
3. Озвучивание целей урока и плана его проведения.
Учитель: Тема нашего урока - решение тригонометрических уравнений. Я думаю, вам будет интересно на уроке.
Цель урока сегодня – вспомнить метод решения простейших тригонометрических уравнений, решение квадратных уравнений и изучить, как с помощью замены тригонометрических функций сводить некоторые тригонометрические уравнения к квадратным.
В начале урока мы вспомним методы решения квадратных уравнений, числовые значения тригонометрических функций, основные формулы тригонометрии, формулы решения простейших тригонометрических уравнений.
После каждого блока заданий будем проводить разноуровневые проверочные работы, задания которых вы будете выбирать самостоятельно, учитывая свои знания, умения и навыки. Проверяем решения, и вы выставляете себе оценку за каждый вид заданий.
После чего познакомимся с тем, как с помощью замены переменных сводить некоторые тригонометрические уравнения к квадратным. Обсудим полученные результаты работы на уроке, оценим индивидуальную работу. Затем получите инструктаж по выполнению домашнего задания и подведем итоги урока. Согласны с таким планом работы? Хорошо! Итак, приступаем.
1.2. Устная работа.
Задачи этапа: создать базу для усвоения понятий, которые будут использованы на уроке.
Содержание этапа:
Учитель: Первое задание для устной работы - решите уравнения:
| Уравнения | Ответ |
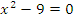 | -3, 3 |
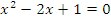 | |
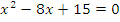 | 3, 5 |
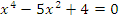 | -2, -1, 1, 2 |
Учитель: Второе задание – используя основные формулы тригонометрии, упростите выражение:
| Выражение | Ответ |
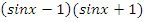 | 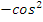 x x |
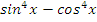 | 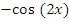 |
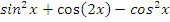 | |
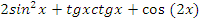 | 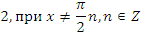 |
Основная часть урока.
2.1. Повторение (чередование фронтальной и индивидуальной форм работы с последующей проверкой задания).
Задачи этапа: обеспечивать развитие у учащихся общеучебных умений и навыков: умение анализировать, синтезировать, сравнивать, обобщать, поиск способов решения, отрабатывать навыки самооценивания знаний и умений, выбора разноуровневого задания.
Содержание этапа:
Учитель: Ребята, давайте вспомним свойства четности и нечетности тригонометрических функций и значения тригонометрических функций для различных чисел.
Учащиеся формулируют свойства четности и нечетности, называют табличные значения тригонометрических функций.
Учитель: А теперь выполним самостоятельную работу. Работа предлагается в 2 вариантах, после чего проверим правильность ее выполнения.
Найдите значения тригонометрических выражений:
| 1 вариант | 2 вариант | ||
| Вычислить | Ответ | Вычислить | Ответ |
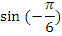 | 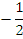 | 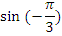 | 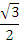 |
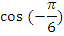 | 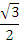 | 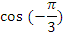 |  |
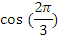 | 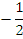 | 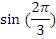 | 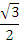 |
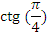 | 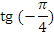 | -1 | |
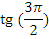 | Нет | 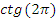 | нет |
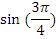 | 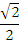 | 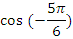 | 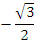 |
Учитель: А теперь сверьте свои ответы с ответами соседа. Сверили. Молодцы!
Учитель: Ребята, проверьте правильность ответов и оцените свои работы согласно шкале:
| Количество верных ответов | Оценка |
| <4 |
Учитель: Ребята, а теперь перейдем к решению простейших тригонометрических уравнений. Напомните, пожалуйста, формулы решения уравнений вида: 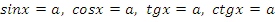 , при
, при 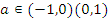 .
.
Учащиеся называют формулы решения уравнений
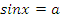 | 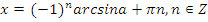 |
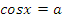 | 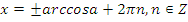 |
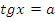 |  |
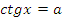 | 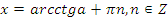 |
2.2. Введение нового способа решения тригонометрических уравнений.
Задачи этапа: организовать деятельность учащихся по применению знаний, умений и навыков при решении тригонометрических уравнений незнакомыми способами.
Содержание этапа:
Учитель: А сейчас познакомимся с решением тригонометрических уравнений новым способом: с помощью замены одной из тригонометрических функций и сведением к квадратному уравнению.
| Вид уравнения | Подходящая замена | |
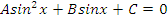 | 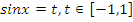 | |
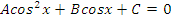 | 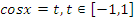 | |
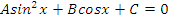 | 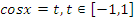 | |
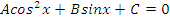 | 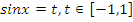 | |
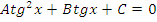 | 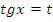 | |
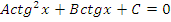 | 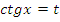 | |
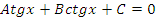 | 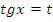 или или 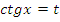 |
В таблице приведены виды тригонометрических уравнений и подходящая замена переменной, с помощью которой данные уравнения могут быть сведены к квадратным. Чтобы не заучивать таблицу, давайте выделим признаки, по которым произвольное тригонометрическое уравнение может быть классифицировано, как уравнение, сводящееся к квадратному.
Первым действием нужно убедиться, что все тригонометрические функции, входящие в уравнение, имеют единый аргумент. Если это не так, то их нужно свести к единому аргументу. Для этого используются формулы блока: “формулы двойного аргумента”
Вторым действием нужно пытаться привести уравнение виду: 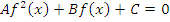 , где
, где 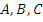 – некоторые числа,
– некоторые числа, 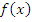 – одна из тригонометрических функций. Для этого используется основное тригонометрическое тождество или взаимосвязь между тангенсом и котангенсом.
– одна из тригонометрических функций. Для этого используется основное тригонометрическое тождество или взаимосвязь между тангенсом и котангенсом.
Третьим действием общая тригонометрическая функция заменяется буквой 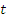 , при этом учитывается область значений обозначаемой функции.
, при этом учитывается область значений обозначаемой функции.
Таким образом, некоторые тригонометрические уравнений могут быть сведены к видам из таблицы.
Учитель: разберем несколько примеров:
1) 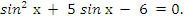
Данное уравнение соответствует (1) таблицы, поэтому делаем замену 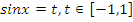 ,
,
· получаем квадратное уравнение: 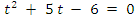 ,
,
· находим корни 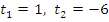 ,
,
· замечаем, что 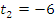 посторонний корень, поскольку
посторонний корень, поскольку 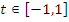 ,
,
· делаем обратную замену, т.е. решаем уравнение 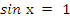 , у которого корнями будут числа
, у которого корнями будут числа 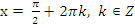 .
.
Ответ: 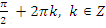 .
.
2) 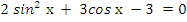 .
.
Данное уравнение соответствует (3) таблицы, поэтому cделаемзамену 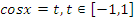 . Из основного тригонометрического тождества следует, что
. Из основного тригонометрического тождества следует, что 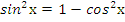 ,
, 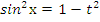 ,
,
· получим квадратное уравнение: 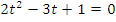 ,
,
· находим корни: 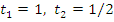 ,
,
· делаем обратную замену:
· 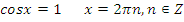 или
или
· 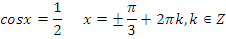
Ответ: 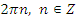 ,
, 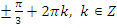 .
.
3) 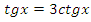 .
.
Данное уравнение соответствует (7) таблицы, поэтому можно сделать замену 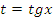 или
или 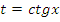 . После решения примера самостоятельно сделайте другую замену и сравните ответы.
. После решения примера самостоятельно сделайте другую замену и сравните ответы.
Сделаем, например, замену 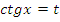 , вспомним, что
, вспомним, что 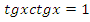 , поэтому
, поэтому 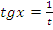 , получим уравнение
, получим уравнение 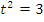 , откуда
, откуда 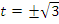 или, делая обратную замену,
или, делая обратную замену, 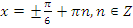 .
.
Ответ: 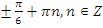 .
.
4) 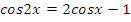 .
.
Данное уравнение непосредственно не имеет вид, описанный в таблице. Как правило, легко классифицировать уравнения, если привести тригонометрические функции в него входящие к одному аргументу. Поскольку 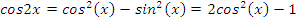 , то уравнение сведено к (2) виду таблицы. Поэтому делаем замену
, то уравнение сведено к (2) виду таблицы. Поэтому делаем замену 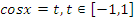 и получаем неполное квадратное уравнение
и получаем неполное квадратное уравнение 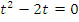 , откуда
, откуда 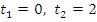 . (
. ( 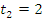 посторонний корень, поскольку
посторонний корень, поскольку 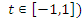 .
.
Делаем обратную замену:
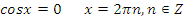
Ответ: 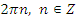 .
.
Учитель: А теперь выберите одно из предложенных уравнений и самостоятельно решите его.
| На оценку | 1 вариант | |
| задание | ответ | |
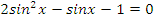 | 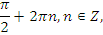 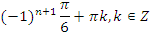 | |
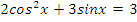 | 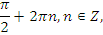 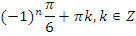 | |
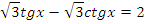 | 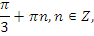 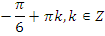 | |
| 2 вариант | ||
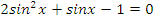 | 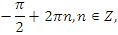 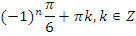 | |
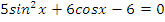 | 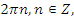 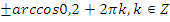 | |
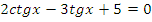 | 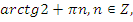 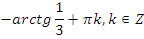 |
Учитель: “А теперь проверьте работу соседа, поставьте оценку”.
Выписываются на доске ответы. Учитель: проверьте правильность собственного решения и правильность проверки примера соседа.
Ход урока
Организационный момент.
Учитель здоровается с учениками, проверяет их готовность к уроку, оглашает цель урока. Учащиеся приветствуют учителя.
Заключение
Основными характеристиками критического мышления, которые можно эффективно развить на уроках математики в школе, является анализ информации с использованием логики, обоснованность и доказательность рассуждений и выводов.
Решение первой задачи, поставленной в исследовании, приводит к следующему выводу. Важнейшей функцией критического мышления является то, что это тип мышления, позволяющий формировать такое качества личности как умение мыслить самостоятельно. Такая характеристика может быть отнесена к высшему уровню развития мышления, т.к. она подразумевает способность подвергать сомнению любую информацию, умение задавать вопросы, проясняющие суть проблемы, требующей разрешения. Далее анализируются имеющиеся средства ее разрешения и при необходимости критически мыслящая личность способна организовать свою деятельность по поиску недостающих знаний, и их применения для разрешения ситуации.
Выводы, полученные в результате решения второй и третьей задач исследования следующие.
Изучение методики преподавания темы «Тригонометрические функции», в методической литературе и разработках учителей, приводит к ряду полезных выводов относительно применимости стратегий развития критического мышления на уроках математики. Во-первых, материал школьной математики, является достаточным источником для развития критического мышления в силу самой структуры математических знаний. Во-вторых, при планировании уроков требуется проанализировать учебные задачи на применимость конкретной стратегии и выбрать наилучшим образом отвечающий поставленной задаче. В-третьих, периодичность использования на уроках стратегий развития критического мышления приводят к привыканию школьников и дисциплине «включения» мышления на уроках математики, что активизирует их стремление самостоятельно справиться с заданием даже при традиционной форме урока. Это является одним из «побочных» эффектов системной работы в этом направлении. В-четвертых, недопустим формальный подход при организации урока с применением методов развития критического мышления, ибо это может вызвать обратный эффект и привести к потере времени и устойчивого отторжения попыток учителя организовать самостоятельную работу школьников над учебным материалом на уроке.
Общий вывод по результатам дипломного исследования заключается в том, что развитие критического мышления школьников на уроках математики, в частности темы «тригонометрические функции» является мощным инструментом не только познания математики, но и становления личности школьников. Именно поэтому применение стратегий его развития на уроках требует систематической работы учителя над изучением и применением стратегий, анализ и постоянное улучшение собственной практики преподавания.
Список литературы
Омарова В.К. - Инновационные подходы в образовании
Загашев И.О. - Критическое мышление технология развития
Мынбаева А.К. - Конгитивные психологии обучения
Введение
Ведущей характеристикой образования сегодня является ее нацеленность на обработку большого количества информации, развитость коммуникативных навыков и готовность личности к переменам.
В этих условиях формирование системы качественного образования граждан представляет собой стратегическую задачу, ввиду того, что конкурентоспособность государства зависит от уровня образованности и развитости каждого. Как показывает опыт стран с высоким уровнем развития системы образования, например, Финляндии, Японии, Сингапура (сегодня в этот список входит и Китай), это быстро сказывается на развитии науки, технологий, следовательно, и на развитии экономики и уровня жизни в этих странах. Одновременно образованность граждан стабилизирует социальную обстановку в обществе, ведь уверенность в будущем базируется на уверенности в том, что человек всегда найдет работу.
Сегодня Казахстан идет по пути реформирования системы образования на всех ее уровнях и становления своей уникальной модели. Одним из принципиальных требований к результатам образования школьников является их способность применять на практике полученные в школе знания, умения и навыки. Одним из отправных моментов для преобразования математической подготовки школьников являются результаты международного тестирования школьников по системе PISA и TIMSS. Эти исследования показывают способность школьников применять знания по математике в повседневной жизни (PISA) и уровень математических знаний (TIMSS). Результаты исследований показали, что наши школьники не владеют умением представления задач, возникающих в повседневности, в виде математической задачи, следовательно, не могут продемонстрировать знания приемов их решения.
Задачи обучения математики в школе не изменились в связи с изменением подходов к формированию математических знаний школьников. Л.Д.Кудрявцев, автор учебников по алгебре и началам анализа, пишет: «Целью при обучении математике является приобретение учащимися определенного круга знаний, умений использовать изученные математические методы, развитие математической интуиции, воспитание математической культуры. ...Для правильной постановки задачи, для оценки ее данных, для выделения существенных из них и для выбора способа ее решения необходимо обладать еще математической интуицией, фантазией и чувством гармонии, позволяющим предвидеть нужный результат, прежде чем он будет получен. В результате приобретенных в процессе обучения математике знаний и интуиции у учащихся появляется то, что обычно называется математической культурой" .
Характеристиками критического мышления являются, как известно, его самостоятельность, умение поставить проблему. Последнее подразумевает сбор информации о том, что известно, что нужно узнать и какие есть для этого средства, а также умения определить чего недостает для решения этой проблемы. На этой основе нужно уметь выбрать оптимальный метод ее решения. Это решение должно быть четко аргументировано. Таким образом, ученик должен уметь защитить свое решение в процессе общения со сверстниками, учителем, экзаменатором. Обладание такими умениями, очевидно, как нельзя лучше формируется в результате обучения математике, ввиду совпадения целей обучения математике с задачами формирования критического мышления школьников.
Актуальность темы исследования «Применение стратегий развития критического мышления при обучении тригонометрическим функциям в школе» обосновывается тем, что сегодня проблема достижения целей обучения математике в школе заключается не в столько в содержании обучения математике, сколько в средствах достижения этой цели. На сегодняшний день развитие критического мышления школьников является одним из эффективных средств, призванных добиться реализации целей обучения математике в школе.
Целью дипломного исследования является реализация стратегии развития критического мышления школьников в процессе обучения тригонометрическим функциям в школе
Объект исследования: процесс обучения тригонометрическим функциям в школе. Предмет исследования: реализация стратегий критического мышления в процессе обучения тригонометрическим функциям в школе.
Задачи исследования:
1. на основе анализа психолого- педагогической литературы раскрыть суть технологии критического мышления;
2. на основе анализа методической литературы раскрыть методику обучения тригонометрическим функциям в школе.
3. На основе изученной методики разработать примеры применения стратегий развития критического мышления школьников на уроках математики при изучении темы: «Тригонометрические функции»
Методы исследования:
- теоретический анализ психолого-педагогической литературы;
- анализ методической литературы по изучению тригонометрических функций в школе;
- педагогические наблюдения;
- беседы;
- изучения педагогической документации и работ учеников;
- анализ результатов учебной деятельности учеников.
Теоретической основой исследования явились труды отечественных и зарубежных педагогов, психологов и методистовОмарова В.К.,Мынбаева А.К., Загашев И.О.
Стратегии развития критического мышления при обучении в школе
1.1 Определение понятия “Критическое мышление”
Мышление, предполагающее проверку предложенных решений с целью определения области их возможного применения, - критическое мышление
Линдсей
Всё наше достоинство – в способности мыслить. Только мысль возносит нас, а не пространство и время, в которых мы ничто. Постараемся мыслить достойно – в этом основа нравственности.
Блез Паскаль
Разумное, рефлексивное мышление, способное выдвинуть новые идей и увидеть новые возможности
Д. Браус, Д Вуд
В английском языке понятие “Критическое мышление” означает умение размышлять над тем, каким образом человек получает знания.
Технология “Развитие критического мышления через чтение и письмо” (РКМЧП) возникла в Америке в 80-ые годы XX столетия. В основу ее положены идей и положения теории Ж. Пиаже об этапах умственного развития ребёнка: Л.С. Выготского о зоне ближайшего развития и о неразрывной связи обучения и общего развития ребёнка; К. Поппера и Р.Пола об основах формирования и развития критического мышления; Э. Браун и И. Бек о метакогнитивном учении.
В западной педагогике одними из основоположников направления “Критическое мышление” являются Халперн Д., Хьюелл Л., Зиглер Д. Дж. Стилл, К.Мередит, Ч. Темпл и др. Неоспоримой заслугой активных разработчиков технологий критического мышления является то, что они смогли “переложить” положения данных теорий на язык практики, причём довели свою работу до уровня педагогической технологии, выделив этапы, методический приёмы и критерии оценки результата. Именно поэтому их разработками может пользоваться огромное количество педагогов, достигая эффективных результатов на работе.
Болонский процесс, Совет Европы объявили, что:
- образование – важнейший приоритет политики государств;
- главная цель европейской школы – формирование критического мышления;
- сохранить единое образовательное пространство.
Критическое мышление:
- способность анализировать информацию с позиции логики, умение выносить обоснованные суждения, решения и применять полученные результаты как к стандартным, так и нестандартным ситуациям, вопросам и проблемам;
- особый вид мышления, имеющий целью оценку идей. Более узко оно связано с проверкой точности утверждений и обоснованностью рассуждении;
- систематическая оценка аргументов, основанная на ясных рациональных критериях;
- особый вид умственной деятельности, позволяющий человеку вынести здравое суждение о предложенной ему точке зрения или модели поведения;
- принятие обдуманных решений о том, как следует поступать и во что верить
- мышление, влекущее к самоусовершенствованию;
- способность ставить новые вопросы, вырабатывать разнообразные аргументы, принимать продуманные решения;
Критическое мышление (Дэвид Клустер):
- критическое мышление есть мышление самостоятельное;
- информация является отправным, а отнюдь не конечным пунктом критического мышления;
- критическое мышление начинается с постановки вопросов и уяснением проблем, которые нужно решать;
- критическое мышление стремится к убедительной аргументации;
- критическое мышление есть мышление социальное;
Интеллектуальные умения критического мышления:
- анализ и выводы
- выдвижение, формулировка, разработка гипотез;
- установление и создание, поиск аналогии, метафор;
- активизация ранее приобретённых знании;
- активизация причинно-следственных отношении;
- анализ значимости;
- сравнение – сопоставление – противопоставление;
- применение в реальных условиях;
- контраргументация
- оценка и её достоверность (валидность)
- обобщение идей;
- изучение других точек зрения
Таким образом, критическое мышление значит “искусство суждения, основанное на критериях”.
1.2 Понятие и сущность “Технологии критического мышления”
Технология “Критическое мышление посредством чтения и письма” – это осмысленный подход, поиск здравого смысла: как рассудить объективно и поступить логично, с учётом как своей точки зрения, так и других мнений, умение отказаться от собственных предубеждении.
Критическое мышление – тот тип мышления, который помогает критический относится к любым утверждениям, не принимать ничего на веру без доказательств, но быть при этом открытым новым идеям, методам. Критическое мышление – необходимое условие свободы выбора, качества прогноза, ответственности за собственные решения. Критическое мышление, способное выдвинуть новые идеи и увидеть новые возможности, весьма существенно при решении проблем.
Технология
