Основанные на отношениях между суждениями

Другой, наряду с категорическим силлогизмом, важнейшей разновидностью необходимых умозаключений, изучаемой в курсе традиционной формальной логики, являются умозаключения на основе отношений между суждениями, при обязательном участии сложных суждений.

Умозаключения на основе отношений между суждениями — это умозаключения, в которых используются сложные суждения, а вывод строится на основе знания свойств логических союзов (пропозициональных связок) и операции отрицания. При этом отвлекаются от структуры простых суждений, рассматривая их в качестве целостных, неделимых элементарных логических объектов, обладающими двумя истинностными значениями — «И» и «Л». В современной формальной логике особенности этих форм умозаключений в обобщенном виде рассматриваются в разделе под названием пропозициональная логика, или логика высказываний.

В настоящем пособии рассматриваются некоторые виды подобных умозаключений, считающиеся основными, наиболее известными. На схеме (см. выше Рис. 20) эти виды умозаключений представлены правой ветвью. Это — 1) условные умозаключения, 2) условно-категорические умозаключения, 3) разделительно-категорические и 4) условно-разделительные, или лемматические умозаключения.

Условные (или чисто условные) умозаключения — это умозаключения, в которых все посылки и заключение являются условными суждениями (импликациями). Простейшей логической формой таких умозаключений может считаться следующая:

А → В

В → С

-----------

А → С

Как видно, в данном примере имеется минимум условных посылок — всего лишь две. Но их может быть гораздо больше, практически любое конечное число. При этом могут встречаться суждения с отрицаниями. Кроме того, антецеденты и консеквенты условных посылок могут быть как простыми, так и сложными суждениями, например:

А → (В v C)

(B v C) → D

D → E

-------------------

A → E

Главное условие, которое должно выполняться для условных умозаключений, заключается в том, чтобы антецедент амии (первыми членами) всех условных посылок, начиная со второй, должны быть консеквенты (вторые члены) предшествующих посылок, а в заключении должна быть импликация, антецедентом которой является антецедент первой посылки, а консеквентом — консеквент последней посылки. Кроме того, чтобы это был не просто логически правильный формальный вывод, учитывающий только логическую структуру посылок и заключения, а именно правильное необходимое умозаключение, необходимо, чтобы все посылки были истинными суждениями.

Вывод в условных умозаключениях основывается на свойстве транзитивности импликации (связи «Если… , то…») как особого двуместного отношения, о чем речь шла выше при рассмотрении умозаключений из суждений с двуместными отношениями.

Пример — рассуждение Н.В. Гоголя:

«… не полюбивши России, не полюбить вам своих братьев,

а не полюбивши своих братье, не возгореться вам любовью к Богу,

а не возгоревшись любовью к Богу, не спастись вам».

Фактически, данное рассуждение Н.В. Гоголя представляет собой своеобразное сокращенное умозаключение, в котором пропущено заключение, а именно суждение — «…не полюбивши России — не спастись вам».

Условно-категорическими умозаключениями называются умозаключения, состоящие из трех суждений, двух посылок и заключения, (отчего их также как и ПКС нередко называют силлогизмами), при этом одна из посылок является условным суждением (импликацией), а другая — суждением, которое является антецедентом или консеквентом условной посылки, взятым в утвердительной или отрицательной форме. Заключением такого умозаключения является суждение, которое занимает место второй части условной посылки, также взятое в утвердительной или отрицательной форме.

В традиционной логике длительное время рассматривали только такие условно-категорические умозаключения, в которых части условных посылок и вторые посылки были именно простыми категорическими суждениями. Отсюда произошло название данного вида умозаключений — условно-категорические. В современной логике рассматриваются любые формы подобных умозаключений с любой сложностью их антецедентов и консеквентов.

Простейшими формами условно категорических умозаключений, также как и формы ПКС называемыми модусами, являются следующие (см. Рис. 27):

1)	2)	3)	4)
А → В   А ----------- В	А → В   А ----------- В	А → В   В ----------- А	А → В   В ----------- А

Рис. 27

Всего простейших форм (модусов) условно-категорического умозаключения — четыре. При этом две из них — это правильные модусы, т.е. гарантирующие истинность заключения при истинности посылок. В таблице на Рис. 27 схемы этих модусов указаны под номерами 1) и 4). Эти модусы имеют специальные латинские на­звания: 1),или по-русски — «модус утверждаю­щий», 4) modus tollens,по-русски — «модус отрицающий».

В самом деле, в модусах типа 1) (modus ponens) от утверждения антецедента ус­ловной посылки во второй посылке в заключении мы переходим к утверждению консеквентна условной посылки. Например:

Если решение обжаловано в кассационном по­рядке, то оно еще не вступило в законную силу.

Решение суда обжаловано в кассационном порядке

----------------------------------------------------------------------------

Следовательно, оно еще не вступило в закон­ную силу

Здесь имеет место переход от утверждения основания к утвер­ждению следствия.

Отрицающий модус (modus tollens), форма которого указана под номером 4), позволяет перейти от отрицания следствия к отри­цанию основания. Например:

Если решение суда обжаловано в кассационном порядке, то оно еще не вступило в за­конную силу

Решение суда вступило в законную силу

--------------------------------------------------------------------- Значит, оно не может быть обжаловано в кассационном порядке

Конечно, что-то может происходить или не происходить и в силу иных обстоятельств, но если имеет место данная причина, то следствие обязательно должно наступить, и если отсутствует след­ствие вообще, то значит, не действует никакая возможная причина, в том числе та, которая указана в соответствующей посылке. Здесь мы имеем дело с необходимой формальной связью, что проверяет­ся следующим образом. Необходимо объединить с помощью конъ­юнкции обе посылки, а затем объединить их с помощью имплика­ции с заключением.

Проделав это, мы имеем следующие формы:

1) для утверждающего модуса:

А → В

А

-----------

В

2) для отрицающего модуса:

А → В

В (=В)

-------------------

А

Построим таблицы истинности для данных форм (Рис. 28):

Таблицы истинности правильных модусов условно-категорических умозаключений
	А	В	А	B	Modus ponens ((А→В) ^ А) →B	Modus tollens ((А→В) ^ В) → А)
	и	и	л	л	и	и	и	и	л	и
	и	л	л	и	л	л	и	л	л	и
	л	и	и	л	и	л	и	и	л	и
	л	л	и	и	и	л	и	и	и	и

Рис. 28

Как видим, в таблицах для обоих вариантов мы получаем общее зна­чение «И», то есть, имеем дело с тождественно-истинными формами.

А это значит, что мы имеем дело с логически необходимо ис­тинными суждениями. Такие суждения являются примерами действия определенных логических законов, а их формы могут считаться правилами вывода, гарантирующи­ми истинность заключений при истинности посылок.

Убедимся в том, что два других модуса данного вида умозаключений не являются правильными, то есть у них возможно при некоторых условиях значение «Л» в соответствующих таблицах истинности (см. Рис. 29).

Таблицы истинности неправильных модусов условно-категорических умозаключений
	А	В	А	B	((А→В) ^ А)→ B	((А→В) ^ В) → А)
	и	и	л	л	и	л	и	и	и	л
	и	л	л	и	л	л	и	л	л	и
	л	и	и	л	и	и	л	и	и	и
	л	л	и	и	и	и	и	и	л	и

Рис. 29

Как видим, в третьей и первой строках для обеих форм, соответственно, мы имеем значение «Л», что говорит о том, что данные формы не являются тождественно-истинными, а значит не выражают логических законов, не могут гарантировать истинности заключения при истинных посылках.

Как правильные, так и неправильные модусы условно-категоричес­ких умозаключений широко применяются в практике наших рассужде­ний. Отрицающий и утверждающий правильные модусы (modus pones, modus tollens) относятся к числу наиболее распространенных правил вывода. Что касается неправильных модусов, то они применяются для формулировки версий, гипотез о событиях, в отношении которых могут отсутствовать данные, на основе которых можно было бы построить рассуждения с использованием только правильных форм умозаключе­ний. Следующий пример относится именно к такой гипотетической ситуации:

Если произошло некоторое событие, то остаются чьи-то следы

Обнаружены следы С.

--------------------------------------------------------------------------------

С. причина события

Данное рассуждение нельзя считать необходимым, а заключение ис­тинным, даже если обе посылки истинны: наличие следов еще не говорит о том, что именно С. совершил нечто, составляющее данное событие.

Разделительно-категорическое умозаключение— это умо­заключение, в котором одна посылка обязательно строго раздели­тельное суждение, а другая (другие) — категорические суждения, являющиеся частями разделительной посылки, взятые в утверди­тельной или отрицательной форме. Название этого вида умозак­лючений также берет свое начало в прошлой практике традицион­ной формальной логики, когда рассматривались только простей­шие варианты этого умозаключения. К их числу относятся следу­ющие два модуса разделительно-категорического умозаключения (Рис. 30):

1)	2)
А v В А ---------- В	< А v В > А -------------- В

Рис. 30

Модус 1) называется утверждающе-отрицающим,или по-латински modus ponendo-tollens,модус 2)называется отрицающе-утверждающим, или— modus tollendo-ponens.

Возможны иные, более сложные варианты подобных умозак­лючений, включающие больше членов строго разделительной по­сылки и, соответственно, большее количество посылок, связанных с этими частями разделительной посылки, например (Рис. 31):

< А v В v C v D >

А

D

-----------------------------

< В v С >

Рис. 31

В отношении данного вида умозаключений следует соблюдать такие требования:

1) в разделительной посылке должна использоваться
исключающая, строго разделительная дизъюнкция, не допускающая одновременной истинности частей разделительной посылки;

2) (требование только для отрицающе-утверждающего модуса) разделительная посылка должна быть закрытым суждением, то есть в ней
должны указываться все без исключения возможные варианты исхода ситуации, в противном случае не будет гарантии, что истинным нужно считать именно отсутствующий член.

Условно-разделительные,или лемматические умозаключения— это умозаключения, в которых одна посылка состоит из двух или более условных суждений, а другая — разделительное суждение (строгое или нестрогое), образованное из оснований или консеквентов условных суждений, взятых в утвердительной или отрицательной форме.

Строго разделительные суждения называются лемматическими, или леммами,например:

Если вы будете говорить правду, люди проклянут вас,

а если будете лгать, вас проклянут боги.

Но вы можете только говорить правду или лгать.

--------------------------------------------------------------------

Значит, вас проклянут люди или боги.

Леммы, состоящие из двух членов, называются дилеммами,из трех членов — трилеммами,и т. д. — полилеммами.

Рассмотрим общие формы некоторых модусов лемматических умозаключений только на примере дилемм. Простейшими модусами дилемм явля­ются умозаключения со следующими формами (Рис. 32):

1)	2)	3)	4)
А → В С → В А v C ---------- В	А → В С → D А v C ----------- В v D	А → В А → C B v C ------------- A	А → В С → D B v D -------------- A v C

Рис. 32

Мы получили четыре варианта дилеммы, которые отличаются между собой наличием или отсутствием отрицаний суждений, а также простыми или сложными суждениями, которые получаются в заключении. Различают дилеммы простые и сложные, созида­тельные (конструктивные) и разрушительные (деструктивные).

Простая конструктивная дилемма— это дилемма, состоящая из двух условных посылок (с разными антецедентами, но одинаковы­ми консеквентами) и одной разделительной посылки, в которой объединены основания (антецеденты) условных посылок. В заключении таких дилемм утверждается консеквент условных посылок. Например:

Если я получу премию, то куплю юбилейное издание Пушкина.

Если я получу гонорар, то куплю юбилейное издание Пушкина.

Я получил премию или гонорар.

------------------------------------------------------------------------------

Я куплю юбилейное издание Пушкина.

Данное рассуждение построено по схеме 1) на Рис. 32.

Простая деструктивная дилемма— это дилемма, условные посылки которой включают одинаковое основание (антецедент), но разные консеквенты, а в разделительной посылке объединены консеквенты, взятые с отрицанием. В заключениях таких дилемм полу­чается отрицание общего антецедента условных посылок. Например:

Если я женюсь на Роберте, то меня ждет скучное существование.

Если я женюсь на Роберте, то для меня на­ступит полный крах.

Я не хочу влачить скучное существование или потерпеть полный крах.

------------------------------------------------------------------------------------------

Я не женюсь на Роберте.

Это пример рассуждения по схеме 3) на Рис 32.

Сложная конструктивная дилемма— это дилемма, условные посылки которой содержат разные основания и разные консеквенты, а в разделительной посылке объединены основания (антецеденты) услов­ных посылок, взятые в утвердительной форме (без дополнительных отри­цаний). Заключением такой дилеммы является сложное разделительное суждение, состоящее из консеквентов условных посылок (Схема 2 на Рис. 32).

Сложная деструктивная дилемма— это дилемма, состоя­щая из двух условных посылок с разными основаниями и разными консеквентами, а разделительная посылка которой состоит из отрицаний консеквентов условных посылок. В заключении такой дилеммы стоит сложное разделительное суждение, образованное из отрицаний антецедентов условных посылок (Схема 4 на Рис. 32).

Дилеммы являются объединением соответству­ющих модусов (утверждающего и отрицающего) условно-катего­рических умозаключений. Они сокращают рассуждение, соединяя в себе сразу по две условных связи суждений.

Глава 4.

ПРАВДОПОДОБНЫЕ ИНДУКТИВНЫЕ

УМОЗАКЛЮЧЕНИЯ

Правдоподобные— это умозаключения, в которых имеет место нестро­гое следование, которое не гарантирует истинности заключения, даже если все посылки истинны. Это не значит, что при этом нарушаются какие-либо логические правила, законы. Данное обстоятельство объяс­няется самой природой таких рассуждений. Более того, познающий человек строит свои умозаключения в отношении малоизвестных пред­метов, начиная именно с данных форм умозаключений.

Различают два основных вида правдоподобных умозаключений — индуктивные умозаключения и умозаключения по аналогии, которые в свою очередь подразделяются на ряд подвидов (см. рис. 33).

Кроме того, к числу правдоподобных умозаключений следует отнести все так называемые неправильные модусы необходимых умозаключений, о которых шла речь в разделах 2.1 и 2.2.

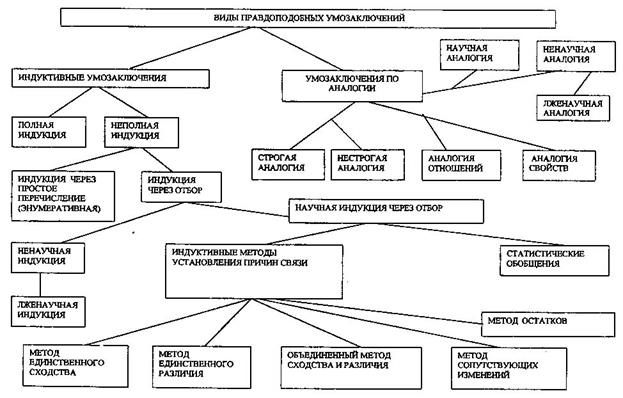
Рис. 33

Индуктивными умозаключенияминазываются такие умо­заключения, в посылках которых содержится знание об отдельных предметах некоторого вида (класса), а в заключении делается вы­вод относительно всех предметов данного вида (класса). Общая структура таких умозаключений выглядит следующим образом (Рис. 34):

а1 есть Р

а2 есть Р

а3 есть Р

……….

аn есть Р

---------------------------------------------------------------

Вероятно, все предметы а обладают свойством Р

Рис. 34

Истинность заключений в индуктивных умозаключениях зависит от знания о количестве предметов, представленного в посылках относительно некоторого признака (Р).

Введем дополнительные обозначения и средства рассмотрения индуктивных умозаключений (см. Рис. 35):

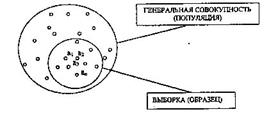
Рис. 35

Вся совокупность (класс) предметов, знания о которых имеется в посылках и заключении индуктивного умозаключения, взятая в целом (в полном объеме), называется генеральной совокупностью, или популяцией.

Совокупность предметов, о которых идет речь в посылках, называется выборкой, или образцом.

Выборка может совпадать или не совпадать с генеральной совокупностью. В зависимости от совпадения или несовпадения выборки и образца различают полную и неполную индукцию.

Полной индукцией называется умозаключение, в посылках которого заключено знание обо всех (о каждом) предметах, входящих в генеральную совокупность. В этом случае выборка совпадает с популяцией. Если все посылки такого умозаключения истинны, то общее суждение, которое получается в заключении будет необходимо истинным. Такую полную индукцию можно отнести к необходимым умозаключениям. Поэтому-то название «дедуктивные умозаключения» для умозаключений, дающих необходимое заключение, нельзя считать точным.

Примером умозаключения является известное всем по школе рассуждение в форме математической индукции (прямой или возвратной).

Применяя полную индукцию, необходимо:

1) точно знать число предметов или явлений, подлежащих изучению и обобщению;

2) убедиться в том, что признак, по которому осуществляется обобщение, принадлежит каждому элементу исследуемого класса предметов или явлений;

3) число изучаемого класса предметов должно быть не очень велико, доступно для проверки каждого из них.

В реальной практике, однако, чаще встречается вариант неполной индукции. Неполная индукция — это индуктивное умозаключение, в посылках которого содержится знание только о части (не обо всех) предметах из генеральной совокупности, а в заключении делается вывод-обобщение относительно всех, каждого предмета из генеральной совокупности. Здесь выборка строго меньше популяции. Именно этот случай и представлен на Рис. 34. Вследствие такого несовпадения заключение в неполной индукции имеет лишь вероятностный характер истинности, т.е. является проблематическим (гипотетическим) суждением по своей эпистемической модальности и поэтому требует дальнейшего обоснования. Т.е. заключение умозаключения неполной индукции может оказаться ложным. При этом, степень, или вероятность истинности заключения неполной индукции может варьироваться в весьма широких пределах — от вероятности, близкой к нулю, до вероятности, близкой к единице.

Рассмотрим далее наиболее характерные разновидности неполной индукции.

Индукция через простое перечисление (энумеративная, или популярная) — это самый слабый по степени обоснованности заключения неполной индукции, который представляет собой вывод на основе случайных примеров предметов, обладающих некоторым признаком. В таком умозаключении, если один и тот же признак повторяется у ряда однородных предметов и отсутствует противоречащий случай, то делается заключение о том, что данный признак присущ всем подобным предметам. Например, вывод о том, что все собаки лают. Позднее у племени пигмеев обнаружили собак, которые не лают. Другим примером такого же рода может служить известный случай о том, что все лебеди белые. В популярной индукции имеет место случайный подбор предметов, без какой-либо системы.

Кстати, для популярной индукции не совсем корректно говорить о выборке (образце) т.к. здесь предметы берутся наугад, из числа первых попавшихся под руку. Хотя иногда выводы по индукции через простое перечисление имеют достаточно очевидный характер. Взять, к примеру, народные приметы, которые формировались в течение сотен, а то и тысяч лет. Такие обобщения представляют собой выводы на основе весьма солидного количества случаев и нередко несут в себе элементы объективного знания: «Ласточки низко летают, значит быть дождю» и т.п.

Индукция через простое перечисление нередко встречается и сегодня, например, когда представителями СМИ делаются заключения весьма общего характера на основе опроса одного или двух десятков прохожих на улице, в каком-либо общественном присутственном месте.

Более обоснованным видом индукции является индукция через отбор.

Индукция через отбор представляет собой индуктивное умозаключение, в основе которого лежит знание об отдельных случаях, отобранных согласно некоторому правилу, принципу, схеме. Такие умозаключения существенным образом исключают (ограничивают) случайность обобщения, т.к. при этом рассматриваются предметы, отобранные по некоторому плану, типичные для данного случая. Степень вероятности заключения в таких умозаключениях может быть даже повышена за счет выполнения ряда вполне осмысленных требований:

1) нужно брать как можно большее количество интересующих экземпляров;

2) отобранные случаи должны быть достаточно разнообразными и отобраны согласно некоторому основанию;

3) интересующий признак должен быть достаточно характерным для данных предметов, типичным;

4) интересующий признак должен касаться существа отобранных предметов.

Ненаучная индукция через отбор является также индуктивным умозаключением, в основе которого лежит отбор предметов на основе житейского опыта, здравого смысла людей. До появления науки такие умозаключения были достаточно распространены и могут считаться наиболее обоснованными для того времени. Именно на основе подобных обобщений формировалась традиционная мудрость.

Особым видом, или метаморфозой ненаучной индукции через отбор, характерной для эпохи, когда уже действует наука и параллельно с научными рассуждениями, является индукция, которую можно назвать «лженаучной индукцией».

Лженаучная индукция через отбор — это рассуждение, напоминающее индукцию через отбор, в посылках которого лежат сведения о специально, тенденциозно, односторонне подобранных случаях, из которых делаются «нужные» в интересах кого-либо обобщения. Чаще всего лженаучная индукция встречается в сфере политической и юридической практики.

Научная индукция через отбор — индуктивные рассуждения, в которых на основании исследования необходимых признаков или необходимой связи признаков части предметов некоторого класса делается заключение в форме гипотетического предположения обо всех предметах данного класса. Например, вывод о том, что «Всем людям для их жизнедеятельности необходима влага». Он сделан на том основании, что: 1) без пищи человек может прожить 30-40 дней, а воду он должен пить ежедневно, в противном случае процесс обезвоживания ведет к необратимым нарушениям внутриклеточного обмена веществ, и как итог — к скорой гибели.

Следует отметить, что научная индукция опирается не столько на количество исследованных предметов, фактов, сколько на всесторонность их анализа и установление причинных зависимостей; на выявление необходимых признаков и их связей.

Особую разновидность научной индукции через отбор представляют собой т.н. индуктивные методы установления причинных связей, в первоначальном виде сформулированные еще в XIX веке Дж.С. Миллем, а также статистические обобщения.

Научные индуктивные методы установления причинных связей представляют собой индуктивные рассуждения, касающиеся причинных зависимостей и связей предметов и явлений, которые опираются на объективное знание природы соответствующих предметов и явлений, доступное в то или иное конкретное историческое время.

Под причинойв науке понимается предмет, явление, которое вызывает к жизни некоторый новый предмет, новое явление. Следствием называется всякая вещь, явление, возникшее в результате действия другого предмета — причины.

Можно назвать несколько объективных признаков причинных зависимостейи связей:

1) действие причины с необходимостью вызывает следствие;

2) если следствие обнаруживается, значит, соответствующая причина имела место;

3) отсутствие следствия указывает на то, что причина, которая его вызывает, не действовала;

4) как причина, так и следствие могут быть сложными; отдельные части сложной причины могут вызывать отдельные части сложного следствия.

Индуктивные методы установления причинных связей позволяют гипотетически заключать о том, какие из предшествующих событий вызывают, обусловливают то или иное новое событие.

Эти методы относят к индуктивным умозаключениям на том основании, что при их использовании из наблюдения некоторых частных случаев делается вывод о закономерностях, проявляющихся для всех подобных случаев.

Традиционно выделяют пять научных индуктивных методов установления причинных связей:

1) метод единственного сходства;

2) метод единственного различия;

3) объединенный метод единственного сходства и различия;

4) метод сопутствующих изменений и

5) метод остатков.

Метод единственного сходства состоит в том, что если два и более случаев имеют общим лишь одно предшествующее обстоятельство, то оно, с вероятностью, является непосредственной причиной данного явления. Схематически это можно выразить так (Рис. 36):

АВСD вызываета

ВСDE вызываета

СFGH вызываета

------------------------------------------------------------

Вероятно, Сесть непосредственная причинаа

Рис. 36

Метод единственного различия заключается в том, что если некоторое сложное явление (причинный комплекс) вызывает некоторое следствие, а другое сложное явление (причинный комплекс), отличающийся от первого лишь одним компонентом — не вызывает следствие, то делается гипотетический вывод о том, что данный компонент причинного комплекса может рассматриваться в качестве непосредственной причины данного следствия (Рис. 37).

АВСD вызывает а

АСD не вызывает а

------------------------------------------------------------

Вероятно,В есть непосредственная причина а

Рис. 37

Объединенный метод единственного сходства и различия — метод, согласно которому если при наличии одного и того же компонента причинного комплекса наступает некоторое следствие, а при его отсутствии — не наступает, то делается вывод о том, что именно этот компонент является непосредственной причиной данного следствия (Рис. 38).

АВСD вызывает а

ВСDE вызывает а

СEFGвызывает а

EFGH не вызывает а

-------------------------------------------------------------

Вероятно, С есть непосредственная причина а

Рис. 38

Метод сопутствующих изменений: если при изменении некоторого компонента причинного комплекса регулярно изменяется некоторое следствие, в то время как остальные компоненты остаются неизменными, то делается вывод о том, что именно этот изменяющийся компонент причинного комплекса является непосредственной причиной данного следствия (Рис. 39).

АВС1D вызывает а1

АВС2D вызывает а2

…………………

АВСnD вызывает аn

------------------------------------------------------------

Вероятно, С есть непосредственная причина а

Рис. 39

Метод остатков позволяет заключать о том, что если сложная причина (причинный комплекс) вызывает некоторое сложное следствие, и при этом установлена причинная зависимость между отдельными компонентами причинного комплекса и компонентами следствия, то делается гипотетический вывод о том, что оставшийся неучтенным компонент причины является непосредственной причиной неучтенного компонента следствия (Рис. 40).

АВСD вызывает abcd

A вызывает d

B вызывает а

D вызывает с

---------------------------------------------------------------

Вероятно, Сесть непосредственная причина b

Рис. 40

Рассмотренные научные индуктивные методы установления причинных связей присутствуют во всех науках. К ним также нередко прибегают и на практике, в частности, в связи с расследованием преступлений, в связи с разработкой и принятием различных управленческих решений.

Глава 5.