Объём подлежащего и сказуемого в суждении
Мы видели, что в разных суждениях то или иное свойство утверждается (отрицается) или относительно одного предмета, или относительно нескольких предметов, или относительно всех предметов данного класса. Иначе говоря, в подлежащем суждения мы отображаем или один, или несколько, или все предметы какого-то определённого класса предметов.
В том случае, когда подлежащее или сказуемое обозначает не все предметы данного класса, а только какую-то часть их, тогда говорят, что подлежащее или сказуемое взято не во всём объёме, или не распределено.
Например, в суждении «Некоторые самолёты имеют реактивные двигатели» подлежащее не распределено, так как в нём говорится о некоторых самолётах, а не о всех.
Когда же подлежащее обозначает все предметы данного класса, тогда говорят, что подлежащее взято во всём объёме, или распределено.
Например, в суждении «Все самолёты тяжелее воздуха» подлежащее распределено, так как в нём говорится о всех самолётах.
Знание распределённости терминов, входящих в суждение, помогает лучше понять смысл самих суждений. Всегда очень важно установить, обозначает ли термин суждения весь класс предметов или только часть класса. Анализ распределённости терминов суждения необходим во всех случаях, когда требуется преобразовать форму у того или иного суждения.
Так, в практике мышления часто приходится общее суждение преобразовывать в частное[3]. Например, общее суждение «Все металлы — элементы» можно преобразовать в частное суждение «Некоторые элементы — металлы».
Но суждение «Все металлы — элементы» нельзя преобразовать в суждение «Все элементы — металлы».
Почему? Потому что термин «элементы» в суждении «Все металлы — элементы» взят не во всём объёме, т. е. не распределён. Поэтому в преобразованной форме суждения, когда термин «элементы» будет обозначать субъект суждения, этот термин нельзя брать во всём объёме.
Знание распределённости терминов, входящих в суждение, даёт возможность более правильно строить наши рассуждения.
Возьмём таких два суждения:
Все одноклеточные размножаются простым делением.
Все амёбы — одноклеточные.
Из сопоставления этих суждений можно сделать следующий вывод:
Все амёбы размножаются простым делением.
В результате данного рассуждения мы пришли к правильному заключению. Больше того, мы получили новое знание в сравнении с тем, которое содержалось в первых двух суждениях.
Но никакого нового знания мы не получим из следующих двух суждений:
Все амёбы — одноклеточные.
Инфузория — одноклеточная.
Почему же из первых двух суждений выводится новое (третье) суждение, а из последних суждений такой вывод невозможен?
Потому, что в первом рассуждении дважды встречающийся термин «одноклеточные» распределён по крайней мере в одном суждении.
Из суждения «Все амёбы — одноклеточные» мы узнаём, что амёбы составляют какую-то часть одноклеточных; из суждения «Инфузория — одноклеточная» мы также узнаём, что инфузории составляют какую-то часть одноклеточных. Но из суждений не видно, каковы же эти части, в каком отношении они находятся друг к другу. А раз так, то термин «одноклеточные» не может так связать термины «все амёбы» и «инфузория», чтобы получилось новое знание.
Из приведённых примеров видно, для чего необходимо знать распределённость терминов в суждении.
Рассмотрим объёмы подлежащего и сказуемого в общеутвердительных, частноутвердительных, общеотрицательных и частноотрицательных суждениях.
1. В общеутвердительных суждениях подлежащее распределено.
Это видно из самой формулы суждения: «Все S суть P», ибо в ней говорится относительно всех представителей того или другого класса. Например, в суждении «Все автомобили имеют двигатели» подлежащее взято во всём объёме, или распределено; все автомобили имеют двигатели.
Сказуемое в общеутвердительных суждениях может быть нераспределённым, а может быть и распределённым.
а) Сказуемое не распределено в тех общеутвердительных суждениях, в которых объём сказуемого шире объёма подлежащего.
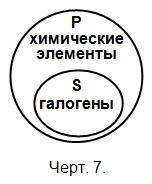
В суждении «Все галогены — химические элементы» сказуемое взято не во всём объёме, ибо в суждении не говорится о всех химических элементах (в том смысле, что все химические элементы суть галогены); другими словами, сказуемое в таком суждении не распределено. Подлежащее в этом суждении представляет собой вид, а сказуемое — род.
Такое отношение между подлежащим и сказуемым суждения можно выразить в виде двух кругов так, как это представлено на чертеже 7.
б) Сказуемое распределено в тех общеутвердительных суждениях, в которых объём сказуемого равен объёму подлежащего.
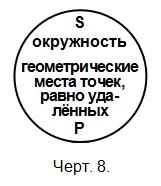
В суждении «Все окружности — геометрические места точек, равно удалённых» сказуемое взято во всём объёме, так как все геометрические места точек, равно удалённых, являются окружностями, и, следовательно, в суждении говорится о всех геометрических местах точек, равно удалённых.
Такое отношение между подлежащим и сказуемым суждения может быть выражено в виде двух совпадающих кругов (черт. 8).
2. В частноутвердительных суждениях подлежащее не распределено.
То, что подлежащее в таком суждении не распределено, очевидно из самой формулы данного суждения: «Некоторые S суть Р». В суждении речь идёт не о всех, а о некоторых предметах, не о всём объёме данного класса предметов.
Например, в суждении «Некоторые рассказы были интересны» сразу видно, что интересны были не все рассказы, а только часть их. Следовательно, подлежащее взято не во всём объёме, оно не распределено.
Сказуемое в частноутвердительном суждении может быть нераспределённым, а может быть и распределённым.
а) Сказуемое не распределено в тех частноутвердительных суждениях, в которых объём сказуемого шире объёма подлежащего.
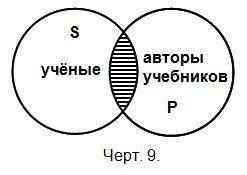
В суждении «Некоторые учёные — авторы учебников» не распределено не только подлежащее, но и сказуемое. В сказуемом мы узнаём не о всех, а только о части учёных. Сказуемое взято не во всём объёме, или не распределено (черт. 9).
б) Сказуемое распределено в тех частноутвердительных суждениях, в которых сказуемое включено в объём подлежащего.
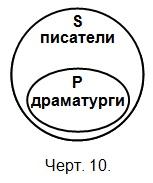
Например, в суждении «Некоторые писатели — драматурги» сказуемое распределено, ибо речь идёт о всех драматургах (черт. 10).
3. В общеотрицательных суждениях и подлежащее, и сказуемое распределены.
Возьмём, например, суждение:
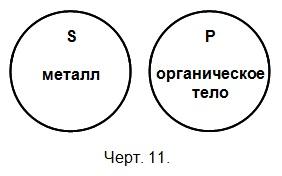
«Ни один металл не есть органическое тело».
Подлежащее в этом суждении распределено, так как мы утверждаем обо всех металлах, что они не являются органическими телами. Это видно из самой формулы общеотрицательного суждения: «Ни одно S не есть Р», ибо сказать «ни одно S» — это равносильно тому, что сказать «все S».
Сказуемое в этом суждении также распределено. Это видно из того, что если ни один металл не есть органическое тело, то и ни одно органическое тело не есть металл. В этом суждении говорится о всех металлах и имеются в виду все органические тела, когда мы исключаем их из группы металлов.
Отношение подлежащего и сказуемого в общеотрицательном суждении можно изобразить в виде двух не соприкасающихся кругов (черт. 11).
4. В частноотрицательных суждениях подлежащее не распределено.
Это ясно видно из самой формулы этого суждения: «Некоторые S не суть Р». В нём речь идёт о части предметов данного класса.
Например, в суждении «Некоторые спортсмены не являются студентами» подлежащее взято не во всём объёме, так как мы говорим о некоторых, а не обо всех спортсменах.
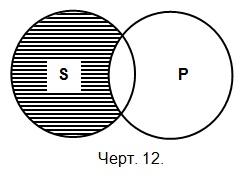
Но сказуемое в этом суждении распределено, так как мы исключаем подлежащее из всего объёма сказуемого. Хотя часть спортсменов входит в число студентов, но остальная часть спортсменов исключается, и притом из всех частей сказуемого.
Графически отношение между подлежащим и сказуемым в частноотрицательном суждении можно изобразить следующим образом (черт. 12).
Так решается вопрос о распределённости подлежащего и сказуемого в общеутвердительном, частноутвердительном, общеотрицательном и частноотрицательном суждениях.
Отношения между суждениями
Материальный мир — это связное, единое целое, где предметы и явления органически связаны друг с другом, зависят друг от друга и обусловливают друг друга.
Естественно, что и между нашими суждениями, в которых отображается материальный мир, должны существовать связи и отношения. И если мы правильно отображаем предметы и связи бытия, отношения и связи между нашими суждениями должны подчиняться определённым закономерностям. Эти закономерности важно знать.
Рассмотрим таких два суждения:
Ни одно растение не может существовать без воздуха.
Цветковые растения не могут существовать без воздуха.
Что характерно для этих двух суждений? То, что предмет, отображаемый в первом суждении (все растения), является подчиняющим в отношении предмета, отображаемого во втором суждении (цветковые растения). Такие суждения находятся в отношении подчинения.
Теперь рассмотрим таких два суждения:
Эта бумага белая.
Эта бумага не белая.
Что характерно для этих суждений? То, что второе суждение полностью отрицает первое суждение. Между ними не может быть ничего среднего: бумага или белая, или не белая. В самом деле, какой бы другой, третий цвет мы ни назвали (синий, красный, голубой и т. д.), он всё равно включается в общее свойство «не белый».
Такие суждения, из которых одно отрицает то же самое, что одновременно утверждает второе об одном и том же предмете, называются противоречащими суждениями. Они составляют первую группу суждений, находящихся в отношении несогласия.
Но отношение несогласия может проявляться и в другой форме. Это легко заметить на примере таких двух суждений:
Эта бумага белая.
Эта бумага чёрная.
Такие суждения называются противоположными суждениями. В данном случае второе суждение отрицает первое суждение, но в отличие от противоречащих суждений второе суждение не ограничивается только отрицанием первого, а одновременно утверждает что-то другое. Мы узнаём, что эта бумага действительно не белая, но одновременно нам стало известно, что бумага чёрная.
Есть ещё и другое отличие. Если в случае противоречащих суждений между ними не может быть среднего, то в данном случае возможны промежуточные суждения: бумага может быть серой, светло-серой, темно-серой и т. д.
Знание отношений между суждениями помогает нам быстрее определять достоверность тех или иных высказываний.
Возьмём такой пример. Допустим, что мы имеем два суждения:
Все ученики нашего класса решили заданные на дом задачи по алгебре.
Некоторые ученики нашего класса не решили заданные на дом задачи по алгебре.
Нетрудно заметить, что данные суждения не могут быть сразу оба истинными. В самом деле, если все ученики решили задачи, то это значит, что нет учеников, которые не решили задач. И наоборот, если хоть один ученик не решил задачи, то нельзя сказать, что все ученики решили задачи.
Следовательно, если истинно первое суждение, то ложно второе; если же истинно второе, то ложно первое; оба эти суждения одновременно не могут быть истинными.
Но эти суждения не могут быть сразу оба и ложными. Действительно, если ложно, что «Все ученики решили заданные задачи», то это значит, что среди учеников были такие, которые не решили заданные задачи, и, следовательно, суждение «Некоторые ученики не решили заданные задачи» истинно. И наоборот, если ложно суждение, что «Некоторые ученики не решили заданные задачи», то это значит, что суждение «Все ученики решили заданные задачи» истинно.
Значит, оба эти суждения одновременно не могут быть ложными. Одно из этих двух суждений должно быть истинным.
Только что разобранные суждения относятся к группе противоречащих суждений.
Можно сформулировать такое правило сопоставления противоречащих суждений:
Два противоречащих суждения не только не могут быть вместе истинными, но они не могут быть вместе и ложными; если одно из противоречащих суждений истинно, то другое ложно.
На противоположные суждения это правило не распространяется.
Возьмём известные уже нам противоположные суждения:
Эта бумага белая.
Эта бумага чёрная.
Оба данных суждения не могут быть истинными. Бумага или белая, или чёрная. Если истинно, что бумага белая, то необходимо вытекает, что суждение «Бумага чёрная» ложно. Но, в отличие от противоречащих суждений, противоположные суждения могут оказаться оба ложными.
Поясним это на таком простом примере.
Допустим, что мы присутствуем при таком споре: один из участников утверждает, что стена древней крепости, которую он видел в Средней Азии, была белой; другой участник спора опровергает это и уверяет, что стена этой крепости была не белой. Это — противоречащие суждения. В процессе спора выясняется, что утверждение первого («стена была белой») ложно. Этого достаточно, чтобы признать суждение второго оппонента («стена была не белой») истинным. Оба такие суждения не могут быть одновременно ложными.
Допустим, мы теперь присутствуем при таком споре: один из участников утверждает, что стена древней крепости была белой, а другой, что стена этой крепости была чёрной. В процессе спора выясняется, что утверждение первого («стена была белая») ложно, но отсюда не вытекает, что стена обязательно была чёрная. Она могла быть и красной, и коричневой и т. д.
Значит, если ложно одно из противоположных суждений, то это отнюдь не значит, что другое истинно. Они оба могут быть ложными.
Можно сформулировать такое правило сопоставления противоположных суждений:
Два противоположных суждения не могут быть вместе истинными, но они оба могут быть ложными; из ложности одного противоположного суждения отнюдь нельзя заключать об истинности другого.
Нам остаётся познакомиться ещё с правилами отношений между подчинёнными суждениями.
Возьмём, например, два таких суждения:
Все жидкости упруги.
Некоторые жидкости упруги.
Предположим, что истинно суждение «Все жидкости упруги». Совершенно очевидно, что подчинённое суждение «Некоторые жидкости упруги» также истинно. При этом следует иметь в виду, что слово «некоторые» понимается в смысле «по крайней мере некоторые». Подчинённое суждение истинно и в случае сопоставления отрицательных суждений.
Если установлено, что «Ни одна сибирская река не течёт на юг», то не может быть сомнений в том, что также истинно и суждение «Некоторые сибирские реки не текут на юг» («по крайней мере некоторые»).
Имеются правила, которые необходимо соблюдать при операциях с суждениями, находящимися в отношениях подчинения:
1. Из истинности общего суждения следует истинность подчинённого ему частного суждения.
Так, например, если истинно суждение «Все галогены — химические элементы», то истинно и суждение «Некоторые галогены — химические элементы».
2. Из ложности частного суждения следует ложность соответствующего общего суждения.
Так, например, если ложно суждение «Некоторые деревья не нуждаются в азоте», то ложно и суждение «Все деревья не нуждаются в азоте».
3. Из истинности частного суждения не следует необходимо истинность соответствующего общего суждения.
Так, например, из истинности суждения «Некоторые ученики нашей школы знают стенографию» вовсе не вытекает истинность соответствующего общего суждения «Все ученики нашей школы знают стенографию».
4. Из ложности общего суждения не вытекает ни ложность, ни истинность подчинённого ему частного суждения.
В самом деле, возьмём такое суждение:
«Все ученики нашего класса увлекаются спортом». Предположим, что это суждение ложно. Что происходит в таком случае с частным суждением? Мы не можем сказать, будет ли истинным или ложным суждение «Некоторые ученики нашего класса увлекаются спортом».
Таковы основные виды отношений между суждениями и некоторые, наиболее часто применяемые в наших высказываниях правила сопоставления различных суждений. Их надо знать, чтобы уметь быстро и безошибочно сделать вывод из сопоставляемых суждений.
Чтобы облегчить запоминание отношений между суждениями, в которых одно и то же подлежащее и сказуемое, но которые имеют разные качества или количества, иногда прибегают к помощи так называемого «логического квадрата».
Схема этого квадрата такова: левый верхний угол обозначается буквой А (общеутвердительное суждение), правый верхний угол — буквой В (общеотрицательное суждение), левый нижний угол обозначается буквой I (частноутвердительное суждение) и правый нижний угол — буквой О (частноотрицательное суждение) (см. черт. 13).
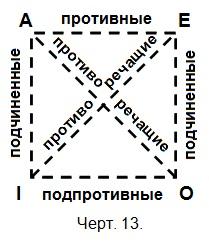
Каждая линия на этом квадрате изображает определённое отношение между двумя видами суждений.
Так, суждения A и I, а также Е и О находятся в отношении подчинения. Это видно и на рисунке: суждение А соединяется с суждением Iлинией, идущей сверху вниз. Суждения А и Е — противоположные или противные. И, наконец, суждения А и О, Е и I — суждения противоречащие. Это отображают линии, которые идут с угла на угол.
Логический квадрат — это средство, облегчающее запоминание. Никакого другого значения логический квадрат не имеет.
Вопросы для повторения
1. Что такое суждение?
2. Из каких частей состоит суждение?
3. В каком отношении находятся части логического суждения к членам грамматического предложения?
4. Дайте примеры единичного утвердительного и единичного отрицательного суждений.
5. Дайте примеры частноутвердительного и общеотрицательного суждений.
6. Какое значение имеют общие суждения?
7. Что такое условное суждение? (Приведите пример условного суждения.)
8. Что такое разделительное суждение? (Приведите пример разделительного суждения.)
9. Дайте пример категорического суждения.
10. Что такое суждение возможности? (Приведите пример суждения возможности.)
11. Что такое суждение действительности? (Приведите пример суждения действительности.)
12. Что такое суждение необходимости? (Приведите пример.)
13. Что означает выражение «распределённость термина»?
14. В каких суждениях распределено подлежащее и в каких суждениях распределено сказуемое?
15. Какие суждения называются тождественными? (Приведите пример.)
16. Какие суждения называются противоречащими? (Приведите пример.)
17. Какие суждения называются противоположными? (Приведите пример.)
Глава VI
ПРЕОБРАЗОВАНИЕ СУЖДЕНИЙ
