Умозаключения по логическому квадрату.

Учитывая свойства отношений между категорическими сужде­ниями А, Е,I, О, которые иллюстрированы схемой логического квад­рата', можно строить выводы, устанавливая следование истинности или ложности одного суждения из истинности или ложности другого суждения.

Рассмотрим эти выводы.

Отношение противоречия (контрадикторности): А — О, Е — I.

Поскольку отношения между противоречащими суждениями подчиняются закону исключенного третьего, из истинности одного суждения следует ложность другого суждения, из ложности одно­го — истинность другого. Например, из истинности общеутверди­тельного суждения (А) «Все народы имеют право на самоопреде­ление» следует ложность частноотрицательного суждения (О) «Не­которые народы не имеют права на самоопределение»; из истин­ности частноутвердительного суждения (I) «Некоторые приговоры суда являются оправдательными» следует ложность общеотрица­тельного суждения (Е) «Ни один приговор суда не является оп­равдательным».

Выводы строятся по схемам:

А -Л О; ~[ А -> О; Е -> 11; -1 Е ->1.

Отношение противоположности (контрарности): А — Е. Из истинности одного суждения следует ложность другого суждения, но из ложности одного из них не следует истинность другого. Напри­мер, из истинности общеутвердительного суждения (А) «Все народы имеют право на самоопределение» следует ложность общеотрица­тельного суждения (Е) «Ни один народ не имеет права на самоопре­деление». Но из ложности суждения А «Все приговоры суда являют­ся оправдательными» не следует истинность суждения Е «Ни один приговор суда не является оправдательным». Это суждение также ложно.

Отношения между противоположными суждениями подчиняют­ся закону непротиворечия. Выводы строятся по схемам: А —Л Е;

E->"lA; lA->(Ev-lE);-lE->(Av-lA).

См рис. 37. С. 87.

Отношение частичной совместимости (субконтрарности):

I — О. Из ложности одного суждения следует истинность другого, но из истинности одного из них может следовать как истинность, так и ложность другого суждения. Истинными могут быть оба суждения. Например, из ложного суждения «Некоторые врачи не имеют меди­цинского образования» следует истинное суждение «Некоторые врачи имеют медицинское образование»', из истинного суждения «Некоторые свидетели допрошены» следует суждение «Некоторые свидетели не допрошены», которое может быть как истинным, так и ложным.

Таким образом, субконтрарные суждения не могут быть вместе ложными; по крайней мере одно из них истинно.

Выводы строятся по схемам:Il->0; "I 0-> I; I -> (OviО);

0->(I v -11).

Отношение подчинения (А —I, Е — О). Из истинности подчиня­ющего суждения следует истинность подчиненного суждения, но не наоборот: из истинности подчиненного суждения истинность подчи­няющего суждения не следует, оно может быть истинным, но может быть ложным. Например, из истинности подчиняющего суждения А «Все врачи имеют медицинское образование» следует истинность подчиненного ему суждения I «Некоторые врачи имеют медицин­ское образование». Из истинного подчиненного суждения «Некото­рые свидетели допрошены» нельзя с необходимостью утверждать об истинности подчиняющего суждения «Все свидетели допрошены».

Выводы строятся по схемам: А —> I;Е —>О; I —> (А v"] А);

0->(Ev-lE).

Из ложности подчиненного суждения следует ложность подчи­няющего суждения, но не наоборот: из ложности подчиняющего суждения ложность подчиненного с необходимостью не следует;

оно может быть истинным, но может быть и ложным. Например, из ложности подчиненного суждения (О) «Некоторые народы не имеют права на самоопределение» следует ложность подчиняющего суждения (Е) «Ни один народ не имеет права на самоопределение». Если ложным является подчиняющее суждение (А) «Все свидетели допрошены», то подчиненное ему суждение (I) «Некоторые свиде­тели допрошены» может быть истинным, но может быть ложным (возможно, что ни один свидетель не допрошен).

В логическом квадрате слово «некоторые» употребляется в значении «по край­ней мере, некоторые».

Выводы строятся по схемам: 11 —>~\А; Ч О -»1 Е; I A —>(I v "II);

nE-^(Ov-lO);

Знание зависимости истинности или ложности одних суждений от истинности или ложности других помогает делать правильные выводы в процессе рассуждения.

Умозаключения по логическому квадрату находят применение во многих мыслительных приемах и операциях, в том числе в аргу­ментации, где построение некоторых способов косвенного доказа­тельства и косвенного опровержения опирается на отношения про­тиворечия.

§3. Простой категорический силлогизм Состав простого категорического силлогизма

Широко распространенным видом опосредствованных умозак­лючений является простой категорический силлогизм, заключение в котором получается из двух категорических суждений. Например, из суждений: 1) «Обвиняемый (S) имеет право на защиту (Р)» и 2) «Гусев (S) — обвиняемый (Р)» следует заключение 3) «Гусев (S) имеет право на защиту (Р)», которое также представляет собой категорическое суждение.

Таким образом, простой категорический силлогизм состоит из трех категорических суждений, два из которых являются посылками, а третье — заключением.

Расчленим суждения, из которых состоит силлогизм, на понятия. Этих понятий три, причем каждое из них входит в состав двух суж­дений «Обвиняемый» — в 1-ю посылку как субъект и во 2-ю посылку как предикат; «имеет право на защиту» — в 1-ю посылку и в заклю­чение как их предикаты; «Гусев» — во 2-ю посылку и в заключение как их субъекты.

В отличие от терминов суждения — субъекта (S) и предиката (Р) — понятия, входящие в состав силлогизма, называюттермина­ми силлогизма. Различают меньший, больший и средний термины.

Меньшим термином силлогизма называется понятие, которое в заключении является субъектом (в нашем примере понятие «Гусев»).Большим термином силлогизма называется понятие, ко­торое в заключении является предикатом («имеет право на защи­ту»). Меньший и больший термины называютсякрайними и обозна­чаются соответственно латинскими буквами S (меньший термин) и Р (больший термин).

Каждый из крайних терминов входит не только в заключение, но и в одну из посылок. Посылка, в которую входит меньший термин, называетсяменьшей посылкой, посылка, в которую входит больший термин, называетсябольшей посылкой. В нашем примере большей посылкой будет первое суждение (1), меньшей — второе сужде­ние (2).

Для удобства анализа силлогизма посылки принято располагать в определенной последовательности: большую — на первом месте, меньшую — на втором. Под чертой записывают заключение:

Обвиняемый имеет право на защиту Гусев —обвиняемый

Гусев имеет право на защиту

Однако в рассуждении такой порядок необязателен. Меньшая посылка может находиться на первом месте, большая — на втором. Иногда посылки стоят после заключения.

Посылки различаются не их местом в силлогизме, а входящими в них терминами.

Вывод в силлогизме был бы невозможен, если бы в нем не было среднего термина.Средним термином силлогизма называется по­нятие, входящее в обе посылки и отсутствующее в заключении (в нашем примере — «обвиняемый»). Средний термин обозначается латинской буквой М (от латинского medius — «средний»).

Средний термин связывает два крайних термина. Отношение крайних терминов (субъекта и предиката) устанавливается благода­ря их отношению к среднему термину. В самом деле, из большей посылки нам известно отношение большего термина к среднему (в нашем примере отношение понятия «имеет право на защиту» к понятию «обвиняемый») из меньшей посылки — отношение мень­шего термина к среднему (понятия «Гусев» к понятию «обвиняе­мый»). Зная отношение крайних терминов к среднему, мы можем установить отношение между крайними терминами (понятиями «Гусев» и «имеет право на защиту»).

Таким образом, вывод из посылок оказывается возможным пото­му, что средний термин выполняет роль связующего звена между двумя крайними терминами силлогизма.

Поставив в нашем примере на место терминов суждения терми­ны силлогизма, получим:

Обвиняемый (М) имеет право на защиту (Р) Гусев (S)—обвиняемый (М)

Гусев (S) имеет право на защиту (Р)

У- 1.1(1;

Итак, простой категорический силлогизм — это умозаключен ние об отношении двух крайних терминов на основании их отноше­ния к среднему термину.

Правомерность вывода, т.е. логического перехода от посылок к заключению, в категорическом силлогизме основывается на положе­нии(аксиоме силлогизма): все, что утверждается или отрицает­ся относительно всех предметов некоторого класса, утверждает­ся или отрицается относительно каждого предмета и любой

части предметов этого класса¹.

В данном примере — все, что утверждается относительно всех обвиняемых, утверждается и относительно конкретного обвиняемо­го (см. в круговых схемах рис. 47).

Рассмотрим силлогизм:

Религиозные организации (М) не выполняют

государственных функций (Р)

Церковь (S) — религиозная организация (М)

Церковь (S) не выполняет государственных функций (Р)

В этом силлогизме все, что отрицается относительно каждой религиозной организации, отрицается и относительно некоторой части этих организаций (рис. 48).

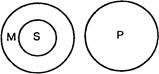
Рис. 47

Рис. 48

' Существует другая, так называемая атрибутивная, формулировка: признак признака некоторой вещи есть признак самой этой веши; то, что противоречит при­знаку вещи, противоречит и вещи.

Общие правила категорического силлогизма

^;^ Из истинных посылок не всегда можно получить истинное заклю-;:

чение. Его истинность обусловлена правилами силлогизма. Этих] правил семь: три относятся к терминам и четыре — к посылкам. ', Правила терминов.

1-е правило: в силлогизме должно быть только три термина.

Вывод в силлогизме основан на отношении двух крайних терминов к среднему, поэтому в нем не может быть ни меньше, ни больше трех терминов. Нарушение этого правила связано с отождествле­нием разных понятий, которые принимаются за одно и рассмат­риваются как средний термин. Этаошибка основана на нарушении требований закона тождества иназывается учетверением терминов.Нельзя, например, получить заключение из посылок: «Законы не создаются людьми» и «Закон — это нормативный акт, принятый высшим органом государственной власти», так как вместо трех терминов мы имеем дело с четырьмя: в первой посылке имеются в виду объективные законы, существующие независимо от сознания людей, во второй — юридический закон, устанавливаемый госу­дарством. Это два разных понятия, которые не могут связать край­ние термины.

2-е правило: средний термин должен быть распределен хотя бы в одной из посылок'. Если средний термин не распределен ни в одной из посылок, то связь между крайними терминами остается неопределенной. Например, в посылках «Некоторые юристы (М—) — члены коллегии адвокатов (Р)», «Все сотрудники нашего коллектива (S) — юристы (М—)» средний термин (М) не распре­делен в большей посылке, так как является субъектом частного суждения, и не распределен в меньшей посылке как предикат ут- ;;

вердительного суждения. Следовательно, средний термин не рас- , пределен ни в одной из посылок, поэтому необходимую связь между крайними терминами (S иР) установить нельзя, что видно из рис. 49, на котором изображены три возможных случая: 1) «Ни один сотрудник нашего коллектива не является членом коллегии адво­катов» (Si); 2) «Некоторые сотрудники нашего коллектива — члены коллегии адвокатов» (82); 3) «Все сотрудники нашего кол­лектива — члены коллегии адвокатов» (S.i).

3-е правило: термин, не распределенный в посылке, не может бЫть распределен и в заключении.

' О распределенности терминов в суждениях см. гл. IV § 2, Распределенн термина обозначается знаком «+», нераспределенность — знаком «-».

Ч

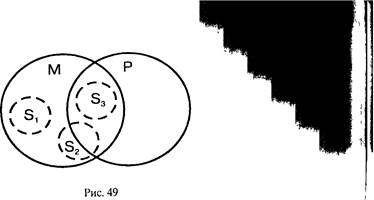
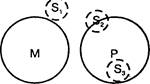
Рис. 50

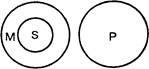
Рис. 51

Например:

Нравственные нормы (М) не санкционируются государством (Р+) Нравственные нормы (М) — формы социальной регуляции (S-)

Некоторые формы социальной регуляции (S-) не санкционируются государством (Р+)

Меньший термин (S) не распределен в посылке (как предикат утвердительного суждения), поэтому он не распределен и в заклю­чении (как субъект частного суждения). Делать вывод с распреде­ленным субъектом в форме общего суждения («Ни одна форма со­циальной регуляции не санкционируется государством») это прави­ло запрещает.Ошибка, связанная с нарушением правила распреде­ленное™ крайних терминов,называется незаконным расширением меньшего (или большего) термина.

Правила посылок.

1-е правило: хотя бы одна из посылок должна быть утверди­тельным суждением. Из двух отрицательных посылок заключение с необходимостью не следует. ,

Например, из посылок «Студенты нашего института (М) не изу­чают биологию (Р)», «Сотрудники НИИ (S) не являются студентами нашего института (М)» нельзя получить необходимого заключения, так как оба крайних термина (S и Р) исключаются из среднего. Поэтому средний термин не может установить определенного отно­шения между крайними терминами. В заключении меньший термин (М) может полностью или частично входить в объем большего тер­мина (Р) или полностью исключаться из него. В соответствии с этим возможны три случая: 1) «Ни один сотрудник НИИ не изучает био­логию (Si); 2) «Некоторые сотрудники НИИ изучают биоло­гию» (Si); 3) «Все сотрудники НИИ изучают биологию» (8э) (рис. 50).

2-е правило: если одна из посылок — отрицательное суждение, то и заключение должно быть отрицательным.

Например:

Судья, являющийся родственником потерпевшего (М), не может участвовать в рассмотрении дела (Р) Судья К. (S) — родственник потерпевшего (М)

Судья К. (S) не может участвовать в рассмотрении дела (Р)

Этот пример показывает, что в силлогизме с одной отрицатель­ной посылкой средний термин исключается из объема крайнего термина (в данном случае — большего), поэтому объем крайнего термина, который входит в объем среднего, исключается из объема другого крайнего термина (рис. 51).

3-е и 4-е правила являются производными, вытекающими из рас­смотренных.

3-е правило: хотя бы одна из посылок должна быть общим суждением. Из двух частных посылок заключение с необходимостью не следует.

Если обе посылки — частноутвердительные суждения (II), то вывод сделать нельзя согласно 2-му правилу терминов: в частно-утвердительном суждении ни субъект, ни предикат не распределе­ны, поэтому и средний термин не распределен ни в одной из посы­лок.

Если обе посылки — частноотрицательные суждения(00), то вывод сделать нельзя согласно 1-му правилу посылок.

Если одна посылка — частноутвердительная, а другая — част-нотрицательная(10 или01), то в таком силлогизме распределенным будет только один термин — предикат частноотрицательного суж­дения. Если этим термином будет средний, то вывода сделать нельзя, так, согласно 2-му правилу посылок, заключение должно быть отри­цательным. Но в этом случае предикат заключения должен быть

распределен, что противоречит 3-му правилу терминов: 1) больший термин, не распределенный в посылке, окажется распределенным в заключении; 2) если же больший термин распределен, то вывода не следует согласно 2-му правилу терминов.

1) Некоторые М(-) суть Р(-) Некоторые S(-) не суть (М+)

2) Некоторые М(-) не суть Р(+) Некоторые S(-) суть М (-)

Ни один из этих случаев не дает необходимых заключений, в чем легко убедиться, подобрав соответствующие примеры.

4-е правило: если одна из посылок — частное суждение, то и заключение должно быть частным.

Если одна посылка общеутвердительная, а другая — частноу-твердительная (AI, IA), то в них распределен только один термин — субъект общеутвердительного суждения.

Согласно 2-му правилу терминов, это должен быть средний тер­мин. Но в таком случае два крайних термина, в том числе меньший, не будут распределены. Поэтому в соответствии с 3 правилом терми­нов меньший термин не будет распределен в заключении, которое будет частным суждением. Например:

Все студенты нашего института (М+) изучают логику (Р-) Некоторые сотрудники милиции (S-) — студенты нашего института (М-)

Некоторые сотрудники милиции (S-) изучают логику (Р-)

Если одна из посылок утвердительная, а другая — отрицатель­ная, причем одна из них частная (EI,АО, ОА), то распределенными окажутся два термина: субъект и предикат общеотрицательного суждения (EI) или субъект общего и предикат частного суждения (АО,ОА). Но в том и другом случае, согласно 2-му правилу посылок, заключение будет отрицательным, т.е. суждением с распределенным предикатом. А так как вторым распределенным термином должен быть средний (2-е правило терминов), то меньший термин в заклю­чении окажется нераспределенным, т.е. заключение будет частным. Например:

Все врачи (Р+) имеют медицинское образование (М-) Некоторые из присутствующих (S-) не имеют медицинского образования (М+)

Некоторые из присутствующих (S-) не врачи (Р+)

Фигуры и модусы категорического силлогизма

В посылках простого категорического силлогизма средний тер­мин может занимать место субъекта или предиката. В зависимости от этого различают четыре разновидности силлогизма, которые на­зывают фигурами (рис. 52).

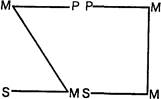
М

-Р Р

-S М

Рис.52

В первой фигуре средний термин занимает место субъекта в боль­шей и место предиката в меньшей посылках.

Во второй фигуре — место предиката в обеих посылках. Втретьей фигуре — место субъекта в обеих посылках.

В четвертой фигуре — место предиката в большей и место субъ­екта в меньшей посылке.

Эти фигуры исчерпывают все возможные комбинации терминов.