Деревья решений - математический аппарат (алгоритм С 4.5).

C4.5. – один из лучших алгоритмов построения деревьев решений.

Прежде чем приступить к описанию алгоритма построения дерева решений, определим обязательные требования к структуре данных и непосредственно к самим данным, при выполнении которых алгоритм C4.5 будет работоспособен:

* Описание атрибутов. Данные, необходимые для работы алгоритма, должны быть представлены в виде плоской таблицы. Вся информация об объектах (далее примеры) из предметной области должна описываться в виде конечного набора признаков (далее атрибуты). Каждый атрибут должен иметь дискретное или числовое значение. Сами атрибуты не должны меняться от примера к примеру, и количество атрибутов должно быть фиксированным для всех примеров.

* Определенные классы. Каждый пример должен быть ассоциирован с конкретным классом, т.е. один из атрибутов должен быть выбран в качестве метки класса.

* Дискретные классы. Классы должны быть дискретными, т.е. иметь конечное число значений. Каждый пример должен однозначно относиться к конкретному классу. Случаи, когда примеры принадлежат к классу с вероятностными оценками, исключаются. Количество классов должно быть значительно меньше количества примеров.

Пусть мы имеем проверку X (в качестве проверки может быть выбран любой атрибут), которая принимает n значений A₁, A₂ ... A_n. Тогда разбиение T по проверке X даст нам подмножества T₁, T₂ ... T_n, при X равном соответственно A₁, A₂… A_n. Единственная доступная нам информация – то, каким образом классы распределены в множестве T и его подмножествах, получаемых при разбиении по X. Именно этим мы и воспользуемся при определении критерия.

Пусть 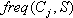– количество примеров из некоторого множества S, относящихся к одному и тому же классу C_j. Тогда вероятность того, что случайно выбранный пример из множества S будет принадлежать к классу C_j

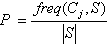
Согласно теории информации, количество содержащейся в сообщении информации, зависит от ее вероятности

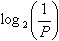(1)

Поскольку мы используем логарифм с двоичным основанием, то выражение (1) дает количественную оценку в битах.

Выражение

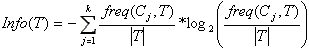(2)

дает оценку среднего количества информации, необходимого для определения класса примера из множества T. В терминологии теории информации выражение (2) называется энтропией множества T.

Ту же оценку, но только уже после разбиения множества T по X, дает следующее выражение:

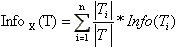(3)

Тогда критерием для выбора атрибута будет являться следующая формула:

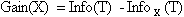(4)

Критерий (4) считается для всех атрибутов. Выбирается атрибут, максимизирующий данное выражение. Этот атрибут будет являться проверкой в текущем узле дерева, а затем по этому атрибуту производится дальнейшее построение дерева. Т.е. в узле будет проверяться значение по этому атрибуту и дальнейшее движение по дереву будет производиться в зависимости от полученного ответа.

Такие же рассуждения можно применить к полученным
подмножествам T₁, T₂ … Tn и продолжить рекурсивно процесс построения дерева, до тех пор, пока в узле не окажутся примеры из одного класса.

Здесь следует пояснить почему критерий (4) должен максимизироваться. Из свойств энтропии нам известно, что максимально возможное значение энтропии достигается в том случае, когда все его сообщения равновероятны. В нашем случае, энтропия (3) достигает своего максимума когда частота появления классов в примерах множества T равновероятна. Нам же необходимо выбрать такой атрибут, чтобы при разбиении по нему один из классов имел наибольшую вероятность появления. Это возможно в том случае, когда энтропия (3) будет иметь минимальное значение и, соответственно, критерий (4) достигнет своего максимума.

Как быть в случае с числовыми атрибутами? Понятно, что следует выбрать некий порог, с которым должны сравниваться все значения атрибута. Пусть числовой атрибут имеет конечное число значений. Обозначим их {v₁, v₂ … v_n}. Предварительно отсортируем все значения. Тогда любое значение, лежащее между v_i и v_i+1, делит все примеры на два множества: те, которые лежат слева от этого значения {v₁, v₂ … v_i}, и те, что справа {v_i+1, v_i+2 … v_n}. В качестве порога можно выбрать среднее между значениями v_i и v_i+1

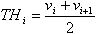
Таким образом, мы существенно упростили задачу нахождения порога, и привели к рассмотрению всего n-1 потенциальных пороговых значений TH₁, TH₂ … TH_n-1.
Формулы (2), (3) и (4) последовательно применяются ко всем потенциальным пороговым значениям и среди них выбирается то, которое дает максимальное значение по критерию (4). Далее это значение сравнивается со значениями критерия (4), подсчитанными для остальных атрибутов. Если выяснится, что среди всех атрибутов данный числовой атрибут имеет максимальное значение по критерию (4), то в качестве проверки выбирается именно он.

Следует отметить, что все числовые тесты являются бинарными, т.е. делят узел дерева на две ветви.