Наследование в теории концептуальных графов.

Нема :(

Машинное обучение на основе связей: введение, основы нейронных сетей.

Нейронные сети – самообучающиеся системы, имитирующие деятельность человеческого мозга.

Искусственный нейрон – имитирует свойства и работу своего биологического прототипа.

Схема нейрона.

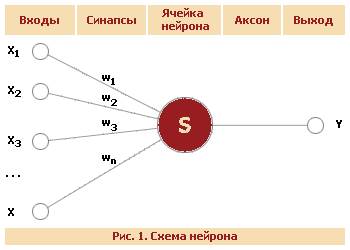
Из рисунка видно, что искусственный нейрон, так же, как и живой, состоит из синапсов (Однонаправленная входная связь нейрона, соединенная с выходом другого нейрона), связывающих входы нейрона с ядром; ядра нейрона, которое осуществляет обработку входных сигналов и аксона (Единственный отросток биологического нейрона, по которому он передает свой выходной сигнал), который связывает нейрон с нейронами следующего слоя. Каждый синапс имеет вес, который определяет, насколько соответствующий вход нейрона влияет на его состояние. Состояние нейрона определяется по формуле:

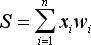, где: n – число входов нейрона, xi – значение i-го входа нейрона, wi – вес i-го синапса.

Затем определяется значение аксона нейрона по формуле: Y = f(S), где f – некоторая функция, которая называется активационной (пороговой). Наиболее часто в качестве активационной функции используется так называемый сигмоид (т.е. функция, график которой похож на букву "S"), который имеет следующий вид:

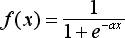
Основное достоинство этой функции в том, что она дифференцируема на всей оси абсцисс и имеет очень простую производную:

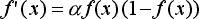
При уменьшении параметра a сигмоид становится более пологим, вырождаясь в горизонтальную линию на уровне 0,5 при a=0. При увеличении a сигмоид все больше приближается к функции единичного скачка.

Обучение нейронных сетей.

Сеть должна для некоторого множества входов давать некоторое желаемое количество выходов каждый из которых рассматривается как вектор. Процесс обучения состоит в том что перебираются входные векторы и подстраиваются их весовые коэффициенты с целью получения определенных результатов.

Существует два способа обучения:

- с учителем

- без учителя

Сети, обучающиеся без учителя, просматривают выборку только один раз. Сети, обучающиеся с учителем, просматривают выборку множество раз, при этом один полный проход по выборке называется эпохой обучения. При обучении с учителем набор исходных данных делят на две части – собственно обучающую выборку и тестовые данные; принцип разделения может быть произвольным. Обучающие данные подаются сети для обучения, а проверочные используются для расчета ошибки сети (проверочные данные никогда для обучения сети не применяются). Таким образом, если на проверочных данных ошибка уменьшается, то сеть действительно выполняет обобщение. Если ошибка на обучающих данных продолжает уменьшаться, а ошибка на тестовых данных увеличивается, значит, сеть перестала выполнять обобщение и просто «запоминает» обучающие данные. Это явление называется переобучением сети или оверфиттингом. В таких случаях обучение обычно прекращают.

Одним из первых ученых который начал разработки в этом направлении был Кохонен. Обучающееся множество состоит из входных векторов. Обучающийся алгоритм подстраивает вес сети так, чтобы получались согласованные выходные векторы, т.е. при предъявлении достаточно близких входных векторов получались одинаковые выходные.

Нейрон Мак-Каллока-Питтса.

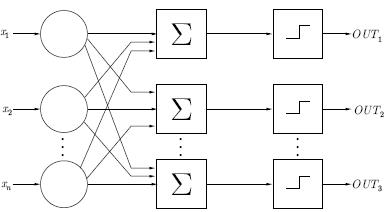
Первым примером нейросетевой модели является нейрон Мак-Каплока-Питтса [McCulloch и Pitts. 1943]. На вход нейрона подаются биполярные сигналы (равные +1 или -1). Активационная функция — это пороговая зависимость, результат которой вычисляется следующим образом. Если взвешенная сумма входов не меньше нуля, выход нейрона принимается равным 1, в противном случае - -1. В своей работе Мак-Калпок и Питгс показали, как на основе таких нейронов можно построить любую логическую функцию. Следовательно, система из таких нейронов обеспечивает полную вычислительную модель.

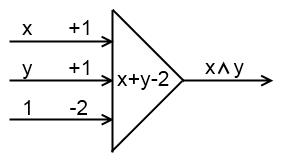
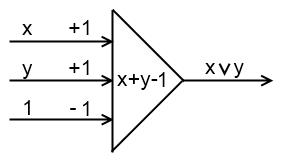
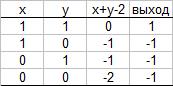
На рисунке показан пример вычисления логических функций И и ИЛИ с помощью нейронов Мак-Каллока-Питгса. Каждый из этих нейронов имеет три входа, первые два из которых задают аргументы функции x и y, а третий, иногда называемый пороговым (bias), всегда равен 1. Весовые коэффициенты связей для входных нейронов составляют соответственно +1, +1 и - 2. Тогда для любых входных значений x и y нейрон вычисляет значение x+y-2. Если это значение меньше 0, выходным значением нейрона является -1, в противном случае 1. Из таблицы видно, что такой нейрон, по существу вычисляет значение функции 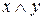. Аналогично можно удостовериться в том, что второй нейрон на рисунке вычисляет значение логической функции ИЛИ.

Несмотря на то что Мак-Каллок и Питгс продемонстрировали возможности нейросетевых вычислений, реальный интерес к этой области проявился только после разработки применимых на практике алгоритмов обучена. Первые модели обучения во многом связаны с работами специалиста по психологии Д. О. Хебба, который в 1949 году предположил, что обучение биологических существ связано с модификацией синапсов в мозгу. Он показал, что многократное возбуждение синапса приводят к повышению его чувствительности и вероятности его возбуждения в будущем. Если некоторый стимул многократно приводит к активизации группы клеток, то между этими клетками возникает сильная ассоциативная связь. Поэтому в будущем подобный стимул приведет к возбуждению тех же связей между нейронами, что в свою очередь обеспечит распознавание стимула. Модель обучения Хебба основана только на идее подкрепления и не учитывает забывчивость, штрафы за ошибки или износ. Современные психолога пытались реализовать модель Хебба, но не смогли получить достаточно общих результатов без добавления механизма забывчивости. Модель обучения Хебба более подробно будет рассмотрена в разделе 10.5.

В следующем разделе модель нейрона Мак-Каллока-Хебба расширена за счет формирования слоен взаимосвязанных нейронов и добавления алгоритмов их взаимодействия. Первая версия такой нейроподобной структуры получила название персептрона (perception).

Персептрон Ф. Розенблата.

В качестве предмета исследования искусственные нейронные сети впервые заявили о себе в 1940-е годы. Стремясь воспроизвести функции человеческого мозга, исследователи создали простые аппаратные (а позже программные) модели биологического нейрона и системы его соединений. Когда нейрофизиологи достигли более глубокого понимания нервной системы человека, эти ранние попытки стали восприниматься как весьма грубые аппроксимации. Тем не менее, на этом пути были достигнуты впечатляющие результаты, стимулировавшие дальнейшие исследования, которые привели к созданию более изощренных сетей.