Понятие логического следования

Выведение следствий из данных посылок — широко распрост­раненная логическая операция. Как известно, условиями истин­ности заключения являются истинность посылок и логическая правильность вывода. Иногда, в ходе доказательства от против­ного, в рассуждении допускаются заведомо ложные посылки (так называемый антитезис при косвенном доказательстве) или при­нимаются посылки недоказанные, однако в дальнейшем эти по­сылки обязательно подлежат исключению.

Человек, не изучавший логику, делает эти выводы, не приме­няя сознательно фигур и правил умозаключения. Формальная логика знакомит с правилами различных видов умозаключений. Математическая логика дает формальный аппарат, с помощью которого в определенных частях логики можно выводить следст­вия из данных посылок. Используя этот аппарат, мы можем, имея некоторые данные, получить из них новые сведения, непо­средственно не очевидные, но заключенные в этой информации, можем выводить логические следствия, вытекающие из данной информации.

Логическое следствие из данных посылок есть высказывание, которое не может быть ложным, когда эти посылки истинны.

Иными словами, некоторое выражение В есть логическое следствие из формулы А (где А и В — обозначения для различных по форме высказываний), если, заменив те конкретные элеме­нтарные высказывания, которые входят в А и В, переменными, мы получим тождественно-истинное выражение (А -> В), или за­кон логики.

Возьмем такой пример. Нам даны три посылки: 1) «Если Иван — брат Марьи или Иван — сын Марьи, то Иван и Ма­рья — родственники»; 2) «Иван и Марья — родственники»; 3) «Иван — не сын Марьи». Можно ли из них вывести логичес­кое следствие, что «Иван — брат Марьи»? Многим сначала ка­жется, что такое логическое заключение из данных трех посылок будет истинным. Чтобы проверить это, следует составить фор­мулу этого умозаключения. Обозначим суждение «Иван — брат Марьи» буквой (переменной) а, суждение «Иван — сын Марьи» — буквой b и суждение «Иван и Марья — родственники» — буквой с.

Запишем нашу задачу символами (над чертой записаны три данные посылки, под чертой — предполагаемое заключение):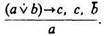

Объединив три посылки в конъюнкцию «л» и присоединив к ним посредством знака « -> » предполагаемое заключение а, получим формулу: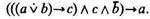

Нам нужно проверить, является ли данная формула, в кото­рой а, b, с трактуются теперь как переменные, законом логики. Составим для этой формулы таблицу (табл. 8).

Таблица 8

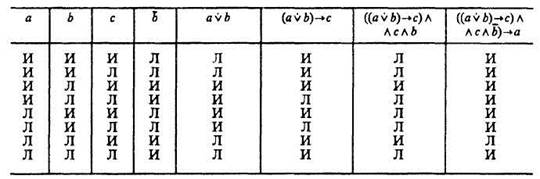
В последней колонке формула в одном случае принимает значение «ложь», значит, она не является законом логики. Следо­вательно, из данных трех посылок не следует с необходимостью заключения, что «Иван — брат Марьи». Иван может быть пле­мянником Марьи, или отцом Марьи, или дядей Марьи, или каким-либо другим ее родственником.

Этот пример показывает, что эффективность средств матема­тической логики видна тогда, когда средствами традиционной формальной логики трудно установить, вытекает ли какое-либо следствие из данных посылок или нет, особенно в случае, когда мы имеем дело с большим числом посылок (но не имеем еще дела с формулами, содержащими кванторы).

Умозаключения делятся на дедуктивные, индуктивные и умо­заключения по аналогии.

В определении дедукции в логике выявляются два подхода. 1. В традиционной (не в математической) логике дедукцией назы­вают умозаключение от знания большей степени общности к но­вому знанию меньшей степени общности. Впервые теория дедукции в этом плане была обстоятельно разработана Аристотелем. 2. В современной математической логике дедукцией называют умозаключение, дающее достоверное (истинное) суждение. Чет­кая фиксация существенного различия классического и современ­ного понимания дедукции особенно важна для решения методо­логических вопросов. Для различения двух смыслов дедукции можно классическое понимание обозначить термином «дедук-ция₁» (сокращенно Д₁), а современное — «дедукция₂» (Д₂).Прави­льно построенному дедуктивному умозаключению присущ необ­ходимый характер логического следования заключения из дан­ных посылок.

ДЕДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ

Дедуктивные умозаключения— те умозаключения, у которых между посылками и заключением имеется отношение логичес­кого следования.

Определение дедуктивного умозаключения, данного в тради­ционной логике (т. е. Д₁), — частный случай из этого определе­ния через логическое следование.

Например,

Все рыбы дышат жабрами. Все окуни — рыбы.

Все окуни дышат жабрами.

Здесь первая посылка «Все рыбы дышат жабрами» является общеутвердительным суждением и выражает большую степень обобщения по сравнению с заключением, также являющимся общеутвердительным суждением «Все окуни дышат жабрами». Мы строим умозаключение от признака, принадлежащего роду («рыба»), к его принадлежности к виду — «окунь», т. е. от обще­го класса к его частному случаю, к подклассу. Частный случай при этом не надо путать с частным суждением вида «Некоторые S есть Р» или «Некоторые S не есть Р».

Понятие правила вывода

Умозаключение дает истинное заключение, если исходные посылки истинны и соблюдены правила вывода. Правила вывода или правила преобразования суждений позволяют переходить от посылок (суждений) определенного вида к заключениям также определенного вида. Например, если в качестве посылок даны два суждения, представимые в виде формулы 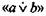и формулы

«о», то можно перейти к суждению вида «b». Это можно путем преобразований по правилу 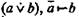в виде формулы записать так: 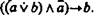Данная формула является законом логики.

Логически правильно можно рассуждать о вопросах, относя­щихся к любым предметам. Логические ошибки также могут быть обнаружены в рассуждениях любого предметного содержа­ния. Из этого не следует, разумеется, что в любых условиях и к любой предметной области должен быть применим один и тот же аппарат формально-логических правил. Сам этот ап­парат должен развиваться вместе с развитием науки и практичес­кой деятельности людей. Одна из характерных черт логики состо­ит в том, что логика позволяет, получив некоторую информа­цию, знания об обстоятельствах дела, извлечь из них — точнее говоря, выявить — содержащиеся в их совокупности новые зна­ния. Так, наблюдая движение Луны и Солнца и делая логические выводы из этих наблюдений (включая и индуктивные обобще­ния), люди еще в античной древности умели логически выводить из них достаточно точные предсказания о наступлении солнечных и лунных затмений.

Другая характерная черта логики, органически связанная с предыдущей, состоит в том, что всякий логический вывод из посылок предполагает некоторую формализацию, т. е. может быть осуществлен по каким-нибудь общим правилам, относя­щимся к способам выражения знаний и способам переработки этих выражений: способам образования и преобразования выра­жений. В зависимости от средств, которыми мы располагаем, таких способов формализации может быть много, начиная с то­го, что одно и то же знание мы можем выразить на разных языках. Но какой-нибудь из языков (под «языком» не обязатель­но понимать звуковую речь) нам необходимо употребить. Без языка, без материального способа выражения мысли невозможно и само мышление.

Формализация способов вывода состоит прежде всего в том, что каждый шаг вывода совершается только в соответствии с каким-нибудь из заранее перечисленных правил вывода, от­носящихся только к способам оперирования с формальными выражениями мысли с помощью материальных знаков. Среди последних имеются специфически логические, так называемые логические константы (постоянные). В математической логике — это конъюнкция, дизъюнкция, отрицание, импликация, эквиваленция, кванторы общности и существования и др.

Различают правила прямого вывода и правила непрямого (кос­венного) вывода. Правила прямого вывода позволяют из име­ющихся истинных посылок получить истинное заключение. Пра­вила непрямого (косвенного) вывода позволяют заключать о правомерности некоторых выводов из правомерности других выводов (эти правила будут проанализированы в § 10 настоящей главы).

Типы дедуктивных умозаключений (выводов) такие: выводы, зависящие от субъектно-предикатной структуры суждений; выводы, основанные на логических связях между суждениями (выводы логики высказываний).

Эти типы выводов и предстоит нам рассмотреть.

Рассмотрим выводы, основанные на субъектно-предикатной структуре суждений.

К формам, типичным в практике рассуждений, относятся следующие выводы из категорических суждений: 1) выводы по­средством преобразования суждений; 2) категорический силло­гизм, сокращенный силлогизм (энтимема), сложные (полисил­логизмы) и сложносокращенные силлогизмы (сориты и эпихейрема).

ВЫВОДЫ ИЗ КАТЕГОРИЧЕСКИХ СУЖДЕНИЙ ПОСРЕДСТВОМ ИХ ПРЕОБРАЗОВАНИЯ

Непосредственными умозаключениями называются дедуктив­ные умозаключения, делаемые из одной посылки. К ним в тради­ционной логике относятся следующие: превращение, обращение, противопоставление предикату и умозаключения по «логичес­кому квадрату».

Превращение

Превращение — вид непосредственного умозаключения, при котором изменяется качество посылки без изменения ее количест­ва, при этом предикат заключения является отрицанием пред­иката посылки.

Как уже отмечалось, по качеству связки («есть» или «не есть») категорические суждения делятся на утвердительные и отрица­тельные.

Схема превращения:

S есть Р.

S не есть не-Р.

При этом частноутвердительное суждение превращается в ча­стно-отрицательное и наоборот, а общеутвердительное суждение превращается в общеотрицательное и наоборот.

Можно выделить два частных способа:

а) путем двойного отрицания, которое ставится перед связкой и перед предикатом:

S есть P. -> S не есть не-Р.

Подлежащие — главные члены предложения. -> Ни одно под­лежащее не является не главным членом предложения;

б) отрицание можно переносить из предиката в связку.

S есть нe-P.-> S не есть Р.Все галогены являются неметаллами. -> Ни один галоген не является металлом.

Превращению подлежат все четыре вида суждения: А, Е, I, О.

1. А -> Е.

Структура: Все S есть Р. -> Ни одно S не есть не-Р. Все волки — хищные животные. -> Ни один волк не является нехищным животным.

2. Е -> А.

Ни одно S не есть Р.-> Все S есть не-Р. Ни один многогранник не является плоской фигурой. -> Все многогранники являются неплоскими фигурами.

3. I -> O.

Некоторые S есть Р.->Некоторые S не есть не-Р. Некоторые грибы съедобны .-> Некоторые грибы не являются несъедобными.

4. O -> I.

Некоторые S не есть Р.-> Некоторые S есть не-Р. Некоторые члены предложения не являются главными. -> Не­которые члены предложения являются неглавными.

Обращение

Обращением называется такое непосредственное умозаключе­ние, в котором в заключении (в новом суждении) субъектом является предикат, а предикатом — субъект исходного суждения, т. е. происходит перемена мест субъекта и предиката при со­хранении качества суждения.

Схема обращения:

S есть Р. Р есть S.

Приведем четыре примера:

1. Все дельфины — млекопитающие.-> Некоторые млекопи­тающие являются дельфинами.

2. Все развернутые углы — углы, стороны которого составля­ют одну прямую.-> Все углы, стороны которого составляют одну прямую, являются развернутыми углами.

3. Некоторые школьники являются филателистами.-> Неко­торые филателисты являются школьниками.

4. Некоторые музыканты — скрипачи.-> Все скрипачи явля­ются музыкантами.

Обращение бывает двух видов: простое, или чистое (примеры 2 и 3), и обращение с ограничением (примеры 1 и 4).

Обращение будет чистое, или простое, тогда, когда и S, и Р исходного суждения либо оба распределены, либо оба не распределены. Обращение с ограничением бывает тогда, когда висходном суждении субъект распределен, а предикат не рас­пределен, или наоборот, S не распределен, а Р распределен.

Примеры

1. Суждение А общеутвердительное.

а) «Все параллельные прямые в геометрии Евклида суть пря­мые, лежащие в одной плоскости и не имеющие общих точек» (определение).

После обращения данное суждение переходит в такое: «Все прямые, лежащие в одной плоскости и не имеющие общих точек, суть параллельные прямые в геометрии Евклида». Это чистое, или простое, обращение;

б) суждение А «Все ели — деревья» обращается с ограничени­ем: «Некоторые деревья есть ели».

2. Суждение Е общеотрицательное.

Так как в нем всегда и S и Р распределены, то его обращение чистое, или простое.

«Ни одна трапеция не является равносторонней фигурой». «Ни одна равносторонняя фигура не является трапецией».

3. Суждение I частноутвердительное. Два случая обращения:

а) обращение чистое, если S и Р нераспределены. Например, суждение «Некоторые растения являются ядовитыми» при об­ращении дает следующее суждение: «Некоторые ядовитые ор­ганизмы являются растениями»;

б) когда объем Р меньше объема S, т. е. Р распределен, a S не распределен, как, например, в суждении «Некоторые музыкан­ты — композиторы», то при обращении имеем суждение: «Все композиторы являются музыкантами».

4. Суждение О частноотрицательное.

Применяя операцию обращения, мы не получим необходимые выводы. Так, например, из истинного частноотрицательного суж­дения «Некоторые животные не являются собаками» путем об­ращения нельзя получить истинного суждения.