К проблеме различия между произвольной компонентой и необходимой частью

Различие между произвольной компонентой (Einzelin­halt) и необходимой частью (Teil) важно во многих отно­шениях; оно исследовалось во многих психологических работах последних десятилетий; многое все еще нуждается в уточнении; необходимо показать это различие на простых контрастных примерах. Здесь приведены некоторые приме­ры, на которых легко показать и изучать отдельные харак­терные особенности проблемы.

1. Нарисуйте на доске группу точек I (a bсd e) и рас­сматривайте их одновременно.

Через короткое время сотрите точки с и е (II).

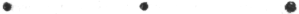
Оставшиеся точки были и раньше на доске, но насколь­ко иначе выглядят они теперь ¹. Рассмотрим некоторые ас­пекты того, что произошло:

Точка d справа в группе I играет ту же роль, какую играет b слева; в II b является «серединой»; а теперь сле­ва является тем, чем d справа.

На языке сетей отношений, в которых каждый произ­вольный элемент имплицитно определяется своим положе­нием в сети, b ¹и d ¹имели (если оставить в стороне разли­чие между правым и левым) одно и то же имплицитное значение, они были «гомологичны». Но b^II является един­ственной центральной точкой, (тем, чем раньше была с^I);

¹ Такое переструктурирование типично для случаев, когда вы­полняются условия хорошего видения, расстояние между точками не слишком велико, и не предпринимаются специальные действия, которые могли бы привести к дезинтеграции. Эти условия сохра­няются и в дальнейших примерах.

d^IIгомологично не b^II, а а^II. Если я обозначу отношение «гомологично» через «~», то в I b~d; d не гомологично а; в II b не гомологично d, d~a.

Сравнивая имплицитные отношения, нельзя даже обо­значать одними и теми же буквами точки в I и II (следует различать b^Iи b^IIи т. д.): содержание II отличается от содержания I.

(В таком исследовании имплицитных связей структур­ные характеристики представлены лишь отчасти; чего-то еще недостает; но то, что здесь подразумевается, можно легко представить аналогичным образом.)

Отличаются также и отношения. Отметим только сле­дующее: в II равенство ab и bd является не только равен­ством двух расстояний, но предполагает и симметрию; од­нако симметрия означает не только равенство расстояний, но содержит существенные характеристики отношений, определяемые свойствами целого.

Рассматривая фигуры, мы замечаем, что объективное равенство аb и bd проявляется в I иначе, чем в П. Часто при восприятии I оно не является даже очевидным (обыч­но при воспроизведении фигуры по памяти обнаруживает­ся эта особенность — подразумевается равенство аb и de, но не аb и bd).

Равенство расстояний аb и bd в II является куда более «чувствительным», чем в I; так, если в I точку d слегка сместить влево (и для сохранения симметрии точку е со­ответственно — вправо), то кажется, что ничего, в сущно­сти, не изменилось; в II же возникнет резкая асимметрия. (Сходные явления наблюдаются при других изменениях: в интенсивности, высоте и т. д.)

Можно, таким образом, видеть, что место и роль от­дельных элементов в целом имеют важное значение для понимания отношений.

2.

d c f

Сотрите c и d (II). Наряду с другими изменениями меняется пространственная ориентация фигуры (фигура наклоняется); ае и bf как параллели определяют фигуру; при нормальном восприятии первой фигуры они обычно не возникают. В I be служит основой для пространствен-

ной ориентации фигуры; в II это не так; в II эта линия часто даже не присутствует перцептивно; если же она и присутствует, то воспринимается как диагональ, гомоло­гичная аf (что не так в I); но быть диагональю — это зна­чит чем-то отличаться от линии симметрии, как в I.

В I а не гомологично 6, f не гомологично е, be не гомо­логично af; во II a~b, f~e, be~af.

3.

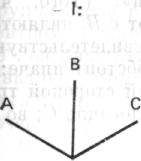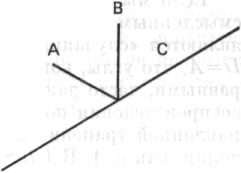Рис. 165 Рис. 166

Удлините оба конца¹ С в I, и вы получите П. В I А и С были «парой», В — линией симметрии; в II («угол АВ стоит на наклонной диагонали») А и В образуют «пару». (В I А~С, А не гомологично В, в II А~В.) В I В явля­ется единственной линией симметрии, определяющей общую пространственную ориентацию фигуры; в II длин­ная наклонная линия обеспечивает основную пространст­венную ориентацию (так же, как и линия — которая не «дана» в качестве элемента, - делящая симметрично угол АВ пополам, перпендикулярная наклонной линии).

В то время как в I фигура чувствительна к нарушени­ям равенства длин A и С, но не к изменению длины В, II чувствительна к нарушениям именно равенства В и А] теперь В=А играет такую же роль, какую раньше играло С=А.

Если для углов принять значение 40° (вместо 60°), то переход к II часто оказывается особенно сильным, и не только в отношении оптических характеристик: «Рисунок «искривился», он «поворачивается»! Рисунок выглядит ужасно!» И в соответствующих условиях часто возникает сильная мотивация, потребность разобраться в ситуации и «исправить дело».

¹ Удлините концы сильнее, чем указано на чертеже.

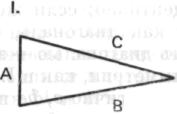
Рис. 167 Рис. 168

Если мы добавим линию D, то она часто кажется бес­смысленным добавлением; ее наличие, длина, ориентация являются «случайными», «произвольными». (Того, что D=A, что углы, которые А и D образуют с 5, являются ровными, часто даже не замечают, о чем свидетельствуют воспроизведения по памяти.) В III дело обстоит иначе: в наклонной трапеции D является наклонной стороной тра­пеции, как и A. В I B~C, в III B не гомологично С; во II

III.

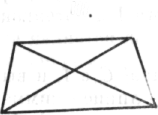
Рис. 169

А не гомологично D, в III A~D. В I В и С являются сто­ронами равнобедренного треугольника; в III В является основанием, С - - диагональю; это существенное различие.

В I равенство В=С иравенство углов, которые В т С образуют с A, являются существенными (чувствительны­ми); в III все это не так; здесь важно равенство диагона­лей и равенство углов, которые А и D образуют с В.

5.

Сначала есть только точки, обозначенные цифрой 1; за­тем добавьте точки, обозначенные цифрой 2, потом через короткое время — точки, обозначенные цифрой 3, и т. д. Когда добавляются точки, обозначенные цифрой 2, то обычно функция «средней точки» остается той же, что и в 1, и т. д.; но через некоторое время: «В правой части точ­ка исчезла!» (ожидание, потребность, требование). Точ­ки 3 предстают в виде на удивление «бессмысленной» на­клонной линии. Когда добавляются точки 4: «Справа воз­никает маленький ромб».

Когда добавляются точки 5 и особенно точки 6, обычно происходит сильная перецентрация: все резко меняется. Группа слева разрушается (ее центр больше не является центром...), характерные особенности всех последователь­но появлявшихся фигур теперь исчезают — все точки со­ставляют одну единую фигуру, являются частями этой фигуры. (Легко перечислить все изменения отдельных точек и т. д.)

В процессе часто проявляются мощные динамически -свойства - возникают конкретные «требования» и действия в соответствии с ними.

6. Дано:

I II

В этих двух мелодиях три ноты и их интервалы иден­тичны как «произвольные компоненты»; для слушателя (и певца) они совершенно различны. В связи с обсуждае­мым вопросом отметим только следующее:

ми в I — тоника   ре-диез в I — основной тон соль в I — малая терция

(фа-бемоль) в II - повы­шение тоники (ми-бемоль) в II — тоника соль в II - большая тер­ция

Музыкальная логика требует различной нотной записи двух тонов: в II нельзя обозначить ми-бемоль как ре-диез (и наоборот).

И интервал между второй и третьей нотами в I являет­ся уменьшенной квартой, а в II — увеличенной терцией! Функциональные различия весьма характерно проявляют­ся при варьировании (изменении высоты тона ноты и т. д. во время пения).

Существенные различия между двумя этими мелодия­ми свидетельствуют также о некоторых совершенно раз­личных тонких характеристиках, но мы не будем входить в дальнейшие детали.

(Вот еще один аналогичный по форме предыдущим пример. Сыграйте сначала следующий мотив:

III

Затем возьмите после первой ноты си и в конце — ми. Тог­да вместо си-бемоль следует написать ля-диез; а вместо ми-бемоль — ре-диез; теперь первая нота является уже не доминантой, а задержанным звуком, который разрешается в доминанту; самая низкая нота является не тоникой, а основным тоном; ведущий к ней интервал больше не тер­ция, а уменьшенная кварта.)

Я провел несколько экспериментов со многими испы­туемыми по решению следующей задачи. Некоторые дети проявляли себя очень хорошо и иногда находили решение после всего лишь минутного обдумывания; другим требо­валась незначительная помощь. Однако некоторые, даже весьма умные и образованные взрослые, действовали до­вольно странно и, пытаясь найти простое решение, испы­тывали большие затруднения.

ПРИЛОЖЕНИЕ 2

Алтарное окно

Я провел несколько экспериментов со многими испытуемыми по решению следующей задачи. Некоторые дети проявляли себя очень хорошо и иногда находили решение после всего лишь минутного обдумывания; другим требовалась незначительная помощь. Однако некоторые, даже весьма умные и образованные взрослые, действовали довольно странно и, пытаясь найти простое решение, испытывали большие затруднения.

Я предлагаю читателю попытаться решить эту задачу.

Художники заняты окраской и отделкой внутренних стен церкви. Немного выше алтаря находится круглое ок­но. В декоративных целях художников попросили прове­сти две вертикальные линии, касательные к кругу и такой же высоты, что и круглое окно;

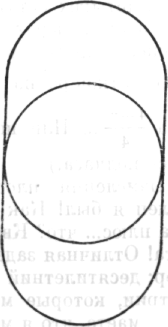
Рис. 170

затем они должны были прибавить снизу и сверху полу­круги, замыкающие фигуру. Эта поверхность между ли-

ниями и окном должна была покрываться золотом. На каждый квадратный дюйм требуется столько-то золота. Сколько потребуется золота для покрытия этой поверхно­сти (при заданном диаметре окна) или чему равна пло­щадь между окном и линиями?

Прежде чем продолжить чтение, попытайтесь найти решение. (Для этого вам не потребуются глубокие знания математики.) Решив задачу, возможно, вы с интересом узнаете об ответах, которые мы получили в экспериментах с этой задачей. Расскажу лишь о некоторых из них. Воз­можно, они доставят вам удовольствие.

Вот, например, слова одного высокообразованного ис­пытуемого: «Конечно, я должен решить ее. Посмотрим... какие теоремы об определении площадей необходимы в данном случае? Несомненно, я должен вспомнить их... Если бы только это был настоящий эллипс (пауза)... но это не эллипс... Если я разделю его, то площади этих час­тей будет легко определить. Внизу и вверху у нас полу­круги, а площадь полукругов я могу легко вычислить. Но есть еще эти четыре забавных кусочка... Какие теоремы я знаю о таких «квазитреугольниках», у которых вместо прямой стороны такой круговой сегмент?.. Не помню ни одной...» И затем после глубокого раздумья он сдался.

Другой испытуемый, столь же сообразительный и с хо­рошей подготовкой по геометрии, действовал аналогичным образом. Но, дойдя до четырех остатков странной формы, он сказал: «Площадь этих четырех фигур равна площади квадрата минус площадь круга, вписанного в квадрат... Площадь

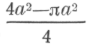каждого из остатков равна	, это равняется а2, умноженное на …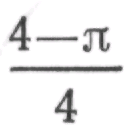
Или не так?.. Правильно? (На это потребовалось полчаса.)

Третий начал с вычисления площади круга и вдруг воскликнул: «Как слеп я был! Как это просто! Площадь равна площади круга плюс... что? Квадрат... круг; это про­сто площадь квадрата! Отличная задача!»

Четвертый пример: десятилетний ребенок без каких-ли­бо знаний по геометрии, которые могли бы ему помочь, сказал: «Почему вы думаете, что я могу сделать это? Я не могу. Не имею ни малейшего представления, как делаются подобные вещи». Он внимательно посмотрел на рисунок, а затем спокойно сказал: «Два полукруга должны войти в «окно... Это полный квадрат». (Он не пользовался термином

«квадрат», а провел по рисунку пальцем.) На все это ушло около минуты.

Пятый: еще один мальчик, двенадцати лет, без какой-либо подготовки по геометрии, начал хвастать тем, как легко он решает такие задачи, и с большой уверенностью высказывал самые дикие предположения. Например: «Че­тыре остатка составляют четверть круга». Я сказал ему: «Не говори чепухи. Подумай немного». Он полминуты мол­чал и затем сказал: «Если вы передвинете два верхних остатка наверх и вставите их в верхний полукруг и если вы проделаете то же самое с нижними остатками, то обе части в совокупности составят квадрат! Вот так».

ПРИЛОЖЕНИЕ 3

Школьный инспектор

Я повторяю то, что подчеркивал в гл. 1 (и в других местах): в любой ситуации имеются элементы или черты, которые являются центральными в структуре, и другие элементы, которые таковыми не являются, будучи перифе­рическими, изменчивыми. Например, абсолютные длины вспомогательных линий параллелограмма связаны со структурной взаимосвязью не больше, чем цвет параллело­грамма.

Увидеть, постичь, понять, что является структурно центральным, а что нет, — вот самое главное во всех слу­чаях мышления. В разделе 14 гл. 1 мы привели пример, когда испытуемым была высказана гипотеза (что последо­вательные произведения возрастают на единицу), не имев­шая ничего общего со структурой, подразумеваемой в за­даче.

Чтобы пояснить этот вопрос, я приведу пример совер­шенно иного рода. Говорят, что эти события произошли в маленькой деревушке в Моравии во времена старой Авст­рийской империи. Однажды сюда приехал инспектор ми­нистерства просвещения. Проведение таких периодических проверок школ входило в его обязанности. Понаблюдав за классом, он в конце урока встал и сказал: «Дети, я рад был видеть, что вы хорошо занимаетесь. У вас хороший класс. Я удовлетворен вашими успехами. И вот, прежде чем уехать, я хочу задать вам один вопрос: «Сколько волос у лошади?» К удивлению учителя и инспектора, один девя­тилетний мальчик очень быстро поднял руку. -Мальчик сказал: «У лошади 3571962 волоса». Инспектор с удивле­нием спросил: «А откуда ты знаешь, что это точное чис­ло?» Мальчик ответил: «Если вы не верите мне, можете сосчитать сами». Инспектор разразился громким смехом, искренне радуясь ответу мальчика. Когда учитель прово­жал его к двери, он, все еще от души смеясь, сказал: «Ка­кая забавная история! Я должен рассказать ее своим кол-

легам по возвращении в Вену. Я уже предвижу, как они воспримут ее; ничто не радует их так, как хорошая шут­ка». И с этим он уехал.

Прошел год, инспектор снова приехал в ту же сельскую школу с ежегодным визитом. Когда учитель провожал его к двери, он остановился и сказал: «Между прочим, госпо­дин инспектор, как понравилась вашим коллегам история с лошадью и количеством волос у нее?» Инспектор похло­пал учителя по спине. «О да, — сказал он. — Видите ли, я действительно хотел рассказать эту историю — это была очень забавная история, — но понимаете, я не смог этого сделать. Когда я вернулся в Вену, то, хоть убейте, никак не смог вспомнить число волос».

Это выдуманная история, по крайней мере я надеюсь, что это так. Я спрашивал многих людей, после того как они прослушали рассказ: «В чем суть этой истории?» Один тип ответа: «Это действительно глупая история; этот ин­спектор мыслил так, что нарушал старые логические раз­личия между существенным и несущественным». Я сказал: «Конечно, но скажите, пожалуйста, что вы понимаете под словом «существенный»?» Большинство людей не могут объяснить это (кроме того, они не чувствуют необходимо­сти в объяснении столь очевидной вещи). А те, кто может, либо делают это очень неуклюже и довольно странно, либо приводят исторические варианты значения слова «несуще­ственный» типа «быть непостоянным» и т. п. и считают во­прос решенным, хотя в действительности это не ответ.

Некоторые отвечают правильно: «Видите ли, не имеет значения, какое количество волос названо в рассказе». Я сказал: «Правильно, но скажите, пожалуйста, почему?» И затем иногда отвечают, что число волос «несуществен­но». «Величина числа никак не связана с основной мыслью рассказа, между ними нет никакой взаимозависимости или, точнее, нет никакой осмысленной внутренней связи между всем рассказом и именно этим числом (нет ρ-отношения). Поэтому число можно варьировать в разумных пределах». Функция этого элемента, его место и роль в структуре ни­как не связаны с тем, каково именно это число. Структу­ра не предъявляет никаких функциональных требований к точности числа. Структурным требованиям удовлетворя­ет здесь любое (большое) число.

А почему этот рассказ часто воспринимается как очень хорошая шутка? Из-за удивления при виде глупой реши­мости придерживаться именно этого числа, как будто его

конкретное значение является релевантным элементом структуры. Смешно видеть столь нелепое поведение ин­спектора. Я мог бы добавить, что некоторых людей это ма­ло волнует; они не могут связать рассказ с реакцией на него; другие же, по-видимому, вообще не задумываются о том, каков был ход мышления инспектора, а говорят о воз­можных чертах его характера.

Такие личностные проблемы весьма важны, но необ­ходим и другой подход: нужно ясно понять, что означает такое поведение со структурной точки зрения. Возможно, появление такой установки мышления является в этих слу­чаях вовсе не вопросом личностной характеристики инди­вида, а тенденцией, созданной определенным типом обра­зования (основанным на определенных тенденциях теоре­тической психологии) и только преувеличенной в подоб­ной шутке.

ПРИЛОЖЕНИЕ 4

Рекомендации для обучения теме «Площадь»

I

Какой способ обучения доказательствам психологиче­ски хорош, а какой плох — это вопросы, которые следует решать эмпирически. Нужно сравнить различные способы обучения, учитывая те трудности, которые возникают при усвоении, запоминании, а также возможности их воспро­изведения и применения к решению других задач. Дело не только в овладении определенными приемами, но также и в ориентации в материале, открытости ума, развитии спо­собностей мыслить.

Это вопросы опыта и экспериментирования. Но следует не просто слепо сравнивать любые приемы обучения, а попытаться изучить эффекты применения противополож­ных приемов в свете нашей главной проблемы: проблемы структурной осмысленности или структурной произволь­ности в самом процессе обучения.

Здесь я намечу один из возможных, психологически осмысленных способов обучения, которым мог бы восполь­зоваться учитель.

Для многих — не для всех—детей желательно начинать с конкретных, реальных жизненных ситуаций, когда предлагаемая задача, скажем определение площади прямо­угольника, является вполне разумным требованием. Это можно сделать, например, рассказав им о двух фермерах, которые обмениваются двумя участками земли, или о фер­мере, который пытается узнать, сколько потребуется зер­на для определенной части его поля, — эти ситуации есте­ственно требуют определения площади.

Для таких детей весьма существенно, есть ли вообще какой-нибудь реальный смысл в постановке данной про­блемы. В качестве иллюстрации могу привести следую­щие примеры.

Двадцать пять лет назад родители девятилетней девоч­ки, мои друзья, сказали мне, что она испытывает большие затруднения в учебе. Дела обстояли настолько плохо, что учитель девочки посоветовал родителям обратиться за со-

ветом к психиатру. Родители привели девочку к профессо­ру Z, известному психиатру и психологу, в то время заве­довавшему психиатрической клиникой. С грустью они сообщили мне о том, что он провел тестирование и посове­товал забрать ее из школы — столь низким был уровень ее развития. Он предложил поместить ее в дом для умственно отсталых детей и в заключение предупредил родителей, что если они не последуют его совету, то ребенок станет неуп­равляемым и, возможно, даже преступником.

Родители не могли последовать такому совету. Они чув­ствовали, что заключение психолога о их ребенке неспра­ведливо: девочка часто проявляла отличный здравый смысл, особенно в реальных жизненных ситуациях, инте­ресовалась искусством. Однако она испытывала трудности в учебе, особенно в арифметике. Низкие результаты тести­рования интеллекта, полученные профессором, вполне согласовывались с ее плохой школьной успеваемостью.

Родителей интересовало мое мнение. Зная ребенка с младенчества, зная, что она была прекрасным здоровым ребенком, я предложил поговорить с ней. Вначале я попро­сил девочку рассказать мне, какие вопросы задавал ей про­фессор Z. Это были обычные вопросы, в том числе и ариф­метические задачи. Я переменил тему разговора. Я расска­зал ей о конкретных событиях, которые якобы произошли в семье соседей, где мать собиралась купать ребенка, не имея подходящих емкостей. Девочка очень заинтересова­лась рассказом, и, когда в драматический момент я задал вопрос: «Что делать?», — она реагировала живо и разумно. И это несмотря на тот факт, что я выбрал вопросы, тре­бующие не только выполнения тех операций, которые про­верял профессор Z, но также и других, более трудных операций. Девочка не могла решать задачи, смысла кото­рых она не понимала. Однако если проблема возникала в конкретной ситуации, если сама ситуация требовала ре­шения, она не испытывала каких-либо особых трудностей, часто демонстрируя присущий ей здравый смысл.

Один из моих друзей, антрополог из Любека, долгое время жил в одном племени в Центральной Африке. По возвращении он показал мне прекрасные вещи, которые привез с собой, и добавил: «Но я должен получить еще не­сколько отличных вещиц. Некоторые из мужчин племени, с которыми я дружил, согласились сделать и прислать мне хижину аборигена, со всей обычной утварью и художест­венными украшениями. Я хотел выставить их в своем му-

зее Они согласились сделать все вещи в треть их обычной величины, так как у меня нет места для экспонатов в пол­ную величину. Я хотел бы показать их тебе, когда они прибудут. Они тебе понравятся».

Несколько месяцев спустя вещи прибыли. Все было в порядке, все предметы были в три раза меньше их обыч­ной величины. Но моего друга удивило несоответствие не­которых деталей. Котелок для приготовления пищи и дере­вянная подставка, которую кладут под голову во время сна, имели натуральную величину.

Антрополог написал письмо одному из своих друзей, миссионеру, который жил с этими людьми, и попросил его по-дружески пожурить их и заставить прислать те несколь­ко предметов в нужной пропорции. Пришлось долго ждать ответа. Он гласил: «Я не смог заставить этих людей вы­полнить заказ. Они настаивали на том, что если человек и может жить в такой маленькой хижине, то было бы бес­смысленно делать горшок для приготовления пищи (н без того достаточно небольшой по размеру) таким маленьким, Так же обстояло дело и в отношении деревянной подстав­ки». Миссионер писал, что он не нашел способа убедить аборигенов выполнить заказ.

Еще один пример: антропологу, работавшему над со­ставлением грамматики языка аборигенов, оказывал по­мощь туземец, который переводил ему различные истории и предложения. Однажды ассистенту нужно было переве­сти какое-то предложение, но антрополог никак не мог добиться от него перевода. Оказавшись в затруднительном положении, он попытался выяснить, какие слова или грам­матические окончания вызывают трудности. И лишь не­которое время спустя туземец выпалил: «Как я могу пере­вести это ваше предложение: «Белый человек убил сегод­ня шесть медведей»? Это чепуха. Белый человек не может убить шесть медведей в один день».

В этих примерах операции, сама цель рассматриваются в тесной связи с функциональным смыслом всей ситуации, их не абстрагируют от той функции, которую они выпол­няют.

Короче, как я уже говорил об этом в исследовании о мышлении примитивных народов ¹, существует большое

¹ См.: Wertheimer M. Über das Denken der Naturvölker, Zahlen und Zahlgebilde.—"Zeitschrift für Psychologie", 1912, Vol. 60, S. 321—378; или Wertheimer M. Drei Abhandlungen zur Ge­stalttheorie. Erlangen, Philosophische Akademie, 1925.

различие между выполнением задания, которое возникает в реальной жизненной ситуации или соответствует ей, и выполнением задания, не связанного ни с какой реальной ситуацией пли даже противоречащего данной ситуации и имеющего смысл лишь при условии, если полностью абст­рагироваться от его роли в реальной жизни.

Но, как я уже отмечал в этой работе, было бы ошибкой делать вывод, что такое неумение абстрагироваться свиде­тельствует об отсутствии способности мыслить. Если кто-то отказывается производить абстракцию, которая кажется ему бессмысленной, если он не может или не хочет иметь дело с такими абстракциями, то это может свидетельство­вать лишь о том, что он серьезно рассматривает конкрет­ную ситуацию. Конечно, в нашей науке абстрагирование от реальности является очень важным инструментом. Но неспособность или отказ выполнять действия, если непо­нятен действительный смысл научного абстрагирования,— это признак не плохого, а хорошего мышления. Неприня­тие тех или иных абстракций само по себе не является критерием оценки мышления. По-настоящему мыслящие люди отказываются, а иногда и не могут выполнить зада­ния, которые предполагают совершенно бессмысленные абстракции, они восстают против них.

Поэтому некоторых детей следует знакомить с геомет­рическими задачами с помощью жизненных ситуаций, в которых само задание имеет для них реальный смысл.

Но есть много детей — и взрослых, — которые не нуж­даются в такой помощи. Их легко заинтересовать «теоре­тическими» проблемами. Они воспринимают проблему как интересное задание, как побуждение к творческой деятель­ности. И, изучая геометрию, они могут и даже жаждут применить то, что они приобрели в результате понимания, к другим геометрическим и жизненным проблемам. Край­ним случаем такой установки являются, конечно, глупые попытки применять такие методы повсюду независимо от того, являются ли они подходящими в данной ситуации.

Я думаю, что задача образования состоит в том, чтобы развивать у детей «теоретический» интерес первого рода. Он открывает им удивительное царство кристальной ясно­сти и внутренней согласованности. И я полагаю, что фор­мальное образование с полным основанием считало, что математика очень важна для развития мышления, тогда даже в практических ситуациях человек не так легко ста­новится жертвой нечеткого, путаного мышления.

II

1. Обращавшиеся ко мне преподаватели математики неоднократно говорили о том, что их не удовлетворяют традиционные методы обучения. Они говорили также, что читали или слышали о моих исследованиях н чувствовали, что они могут помочь им преподавать более осмысленно. Но они не знали, как это можно сделать, как можно разра­ботать конкретную методику обучения в свете гештальт-теории.

Я склонен считать, что основные позитивные выводы в отношении обучения уже содержались в предыдущих гла­вах этой книги. Здесь я попытаюсь изложить один метод, который отвечает моим теоретическим построениям. Но я сразу же скажу: есть хорошие учителя, которые поступа­ют сходным образом, интуитивно чувствуя, каким должно быть обучение. Большая часть того, что я предложу, нико­им образом не является совершенно «новым». Но мой ме­тод, конечно, во многом отличается от тех методов, кото­рые применяются во многих школах.

Существует мною хороших методов, и иногда различ­ные дети нуждаются в разных (хотя и структурно сход­ных) подходах. Легче всего, конечно, учить одного ребен­ка. Здесь я буду говорить о таком обучении. Однако вполне возможно, а иногда и весьма желательно использовать ме­тод группового мышления в классе.

Мой собственный опыт преподавания свидетельствует о том, что лучше всего — особенно поначалу — как можно меньше показывать, «учить». Желательно также, насколь­ко возможно, не давать готовых ответов. Ребенок должен сам прийти к задачам, которые он будет пытаться решить. Пусть он столкнется с проблемами, пусть получит помощь от преподавателя, когда она ему понадобится, но пусть он не просто копирует или повторяет показанные действия. Я бы по возможности избегал всего, что может привести к механизации обучения, к установке на механическое по­вторение.

Проиллюстрирую сказанное на примере определения площади какой-либо фигуры. Важнее всего, чтобы ребе­нок, оказавшись в структурно осмысленной проблемной ситуации, сам нашел свой метод. Если ребенок теряется и говорит: «Я не могу этого сделать», то часто достаточно просто сказать: «Постарайся, возможно, ты и найдешь вы­ход». А если это не помогает, можно дополнительно спро-

сить: «Что тебе мешает?» И только в том случае, если эти меры не помогут, следует оказать конкретную помощь.

2. Осмысленный способ введения понятия «величина площади» прямоугольника. Я бы не начинал с объяснения того, как определить площадь прямоугольника, в особенно­сти с конкретного определения. Потому что смысл поня­тия «величина площади» может быть совершенно непоня­тен ребенку. Я бы скорее начал с ситуации, которая осмыс­ленно связана с проблемой «больше» или «меньше».

Например, я дал бы ребенку два прямоугольника с одинаковыми основаниями, один из которых явно выше другого. И я бы спросил: «Как можно точно определить,

Рис. 171

насколько второй прямоугольник больше первого?» Есте­ственно, не проводя вспомогательной линии. Я бы вырезал из картона два прямоугольника и положил рядом, чтобы ребенок мог прийти к мысли положить один прямоуголь­ник на другой, совместить их и увидеть остаток.

Затем я бы обратился к реальному измерению. «Эта фигура, как видите, имеет 9 дюймов в ширину, такую же ширину имеет и вторая фигура. Далее, высота одной фигу­ры равна 5, а второй - 6 дюймам». И я вначале обрадовал­ся бы, услышав, что ребенок просто говорит: «Один пря­моугольник больше другого на одну полоску или на одну полоску, ширина которой равна 9 дюймам, а высота — 1 дюйму».

2а. Здесь я могу прервать рассказ. Для многих детей эта абстрактная процедура является, как было сказано выше, вполне доступной. С другими детьми желательно начинать с проблемной ситуации, в которой они смогут почувствовать конкретный смысл задачи. Например, я мог бы начать со следующей истории: «Жил-был фермер (или еще лучше для некоторых детей добавить: «По соседству, несколько дней тому назад»), который хотел переехать в другое место. Он нашел фермера, который готов был обме­няться с ним участком. Обе фермы были во многом похо-

жи и были почти одинакового размера. Договариваясь об обмене, фермеры хотели точно определить, действительно ли одна из ферм больше другой, и насколько. Вот рисунок этих двух ферм.

Рис. 172

А теперь скажи, как мы можем узнать, какая из ферм больше?»

Вместо ответа ребенок может задать вопрос, например: «А хватит ли у фермера, у которого ферма меньше, денег, чтобы уплатить разницу?» Но в большинстве случаев мож­но легко поставить ребенка перед проблемой сравнения этих фигур.

2б. Если это не помогает, можно попробовать еще одну конкретную ситуацию, предполагающую более конкретную помощь. «Ты сидишь на полу с другим мальчиком, и каж­дый из вас строит стенку из кубиков. Ты уже использовал все свои кубики, а у другого мальчика еще целая куча неиспользованных кубиков. Тебе очень хочется построить свою стену на один кубик выше, и ты просишь у другого мальчика несколько кубиков. Он отказывается дать их тебе, и ты ему говоришь: «Мне нужно не много, у тебя очень много кубиков, которые тебе не нужны, почему ты не можешь дать мне несколько?» Тот сердито отвечает: «Сколько тебе нужно?» Ну, так сколько кубиков тебе по­надобится, если ты хочешь построить стену на один или два кубика выше?»

Некоторых учителей может испугать смешение трех­мерных и двумерных объектов. Можно, конечно, начать с картонных квадратиков, но, по-моему, это не имеет значе­ния, лично я предпочитаю пользоваться кубиками.

3. Как прийти к «формуле». При помощи таких зада­ний — и еще лучше, если только возможно, при помощи чисто абстрактных заданий — я бы постарался добиться, чтобы ребенок сам пришел к формулировке: «Мне нужен еще один ряд (или еще два ряда и т. д.). Мне нужно столь-

ко-то рядов, я число рядов должно быть умножено на чис­ло кубиков в одном ряду».

Рис. 173

Затем я спросил бы: «Сколько маленьких квадратиков во всей этой фигуре?» (Или: «Чему равна вся площадь?») Ребенок мог бы тогда ответить: «Нужно измерить основа­ние, нужно измерить высоту и перемножить их».

4. Здесь я позволил бы ребенку обнаружить, что можно действовать и так, и эдак независимо от того, какую сторо­ну принять за основание.

Рис. 174

Часто приятно наблюдать, как ребенок радуется, когда узнает, что возможны оба варианта. При определенных ус­ловиях обнаружение того, что аb = bа, является подлинным открытием, подобным инсайту.

5. Задачи на обсуждаемую тему. Я бы не стал продол­жать вычисления на слишком большом числе других при­меров этого типа, опасаясь, что ребенок может забыть структурную формулу. Вместо этого я дал бы вначале не­сколько интересных различных примеров. И я бы привел еще один пример, к которому описанный метод неприме­ним, ожидая, пока ребенок сам не сделает вывод: «Я не могу решить эту задачу тем же способом, здесь нужно со­считать маленькие квадратики». Я бы дал задания, напри-

мер, на определение размера комнаты или двух столов или даже на определение кубического объема комнаты или объема трехмерной коробки, заполненной кубиками. В этой задаче внимание сосредоточивается на количестве кубиков в одном квадрате, которое нужно умножить на высоту, а не просто на умножении сторон.

6. Площадь параллелограмма. Лучше всего просто спросить: «Какова площадь этой фигуры? Можешь ли ты ее определить?» Как и в случае с прямоугольником, неко­торые дети, немного подумав и при поддержке учителя, са­ми находят решение.

Если ребенок не продвигается вперед, можно спросить; «Что тебе мешает? Почему это так трудно сделать?» На что ребенок может ответить: «Трудность связана вот с этими концами. Если бы они были такими же, как у пря­моугольника, все было бы хорошо».

6а. В некоторых случаях полезно дать следующую фигуру:

Рис. 175

Иногда дети отвечают: «О, посередине все хорошо, но...»

6б. Или: «Вот домик из кубиков с прямоугольной верх­ней частью. Мне хотелось бы сделать для него красивую крышу. Вот у меня кусочек красно-коричневого картона. Может быть, его можно использовать. Длина картона та­кая же, как и у верхней части домика, но, к сожалению, она имеет форму параллелограмма. Можешь ли ты сделать из нее крышу нужно