Определение суммы углов многоугольника

1. Во время беседы об орнаментах, которая происхо­дила за ленчем, зашла речь о замкнутых геометрических фигурах, таких, как треугольники, прямоугольники, шес­тиугольники и другие многоугольники. В какой-то момент мой друг, художник, заметил: «Сумма углов всех таких

Рис. 135

фигур, конечно, должна быть одной и той же». Все рас­смеялись. Я оказался в удивительном положении. Я ска­зал: «Конечно же, сумма углов не одна и та же. В тре­угольнике она равна 180°, в прямоугольнике — 360°, в шестиугольнике — 720°». Но я чувствовал, что то утвер­ждение в каком-то смысле должно быть верным, оно за­трагивает какой-то важный момент. Это чувство не поки­дало меня. С одной стороны, было ясно, что сумма углов различных многоугольников не является одинаковой; с другой, я чувствовал, что не могу совсем оставить этот вопрос: ведь должен быть какой-то путь его решения. В этом был какой-то глубокий смысл, но я не знал, как его обнаружить. Невозможно было понять или даже по­чувствовать, в чем же именно заключается проблема. Навязчиво продолжал звучать вопрос: «Должно быть какое-то решение. В чем, черт возьми, дело?»

Другие гости, принимавшие участие в разговоре, не испытывали никакого беспокойства. Вопрос для них был

исчерпан, когда они узнали, что утверждение оказалось явно ложным.

На протяжении нескольких последующих часов, в те­чение которых я должен был заниматься другими веща­ми, проблема продолжала меня волновать. Затем она приобрела такую форму: «С одной стороны, есть А — сум­ма углов фигуры, с другой, В — связанная с замкнутостью завершенность фигуры. Между А и В есть только «и»,

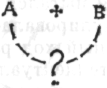
Рис. 136

простая конъюнкция. Вот одно, вот другое. Что кроется за этим «и»-отношением? Что вызывает беспокойство? А и В должны быть как-то связаны друг с другом». Это не было ощущением противоречивости двух утверждений. Я задал себе вопрос: «Как можно это понять?»

2. На следующий день, когда я был занят другой ра­ботой, мне неожиданно пришла в голову следующая смут­ная, неопределенная и неясная идея: «Возьмем точку. Вокруг точки находится полное «угловое пространство» в 360° (один полный угол). Не должно ли происходить

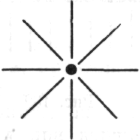
Рис. 137

нечто подобное в случае замкнутой фигуры?» Но в то время я не мог уловить эту крайне туманную мысль.

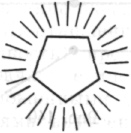
Рис. 138

Прошло три дня. Что бы я ни делал, я все время ис­пытывал одно и то же сильное чувство, ощущение чего-то незаконченного, направленность на что-то такое, что я не мог понять. Несколько раз я чувствовал, что почти что могу сказать, в чем заключается причина беспокойства, от чего оно зависит, в каком направлении следует искать решение, но все было весьма неопределенно, так что я не мог это точно сформулировать. Много раз проблема казалась настолько ясной, что «необходимо было только записать ее», но, когда я пытался это сделать, мне это не удавалось, идея не формулировалась.

(Я обнаружил подобный ход развития во многих дей­ствительно великих интеллектуальных свершениях — то же чувство направленного напряжения при туманности, неопределенности реальной ситуации. В каком-то смысле форма, которую примет решение, «вертится на кончике языка», но ее невозможно ухватить. Это состояние может продолжаться в течение многих месяцев, сопровождаясь многодневной депрессией, и, хотя очевидно, что успех не­значителен, человек не может оставить проблему.)

3. Через два дня снова возник вопрос: «Если я возьму точку, то вокруг нее будет полный угол. Если я возьму прямую линию, то и вокруг нее существует угловое про­странство. Тогда, имея такую прямую линию, как я дол­жен действовать, чтобы получить замкнутую фигуру?

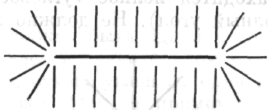
Рис. 139

Просто продолжая прямую линию? Вовсе нет. Я должен изогнуть линию в какой-то точке, если хочу получить замкнутую фигуру». Это быстро привело к идее: «Давай-

Рис. 140

те сначала рассмотрим сумму внешних углов». И что получится? Изгибаясь, угол в 180° разбивается на два «боковых угла», каждый из которых является прямым, и между ними появляется дельта (δ), «угол вращения». Важны именно дельты, вращение.

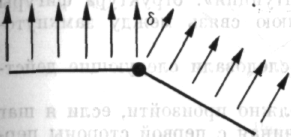
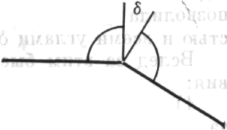
Рис. 141 Рис. 142

И в целой фигуре по мере ее замыкания сумма дельт должна быть равна... полному обороту, углу в 360°, независимо от того, сколько у фигуры боковых сто­рон!

Каждая сторона имеет два внешних прямых угла, по одному на каждом конце. Может быть столько сторон и, следовательно, столько углов, сколько мы пожелаем; но в каждой фигуре углы вращения должны в сумме состав­лять полный угол. Это было «интуицией». В этот момент я чувствовал себя очень счастливым. Я чувствовал: «Те­перь я понимаю, в чем дело».

Что же, в сущности, произошло? Я начал с обычного представления об углах и о завершенности или замкну­тости. Я пытался понять, как возникает замкнутость; полный внешний угол при вершине превратился в два прямых угла плюс δ; я перестал связывать прямые углы с центральной идеей замкнутости, угол δ теперь рассмат­ривается вместе с другими δ в качестве угла, образующе­го полный угол вращения. При таком понимании углов важные углы δ неожиданно оказались связанными с зам­кнутостью фигуры. «И»-отношение А (сумма углов) и В (замкнутая завершенность) превратилось в согласован­ное, понятное, прозрачное единство. А и В больше не были просто рядоположенными отдельными вещами, те­перь они стали частями внутреннего единства. Замыка-

ние фигуры потребовало, чтобы δ дополнили друг друга до 360°. Этот процесс интеграции стал решением: то, что раньше было просто какой-то туманной и неудовлетвори­тельной суммой, теперь приобрело вполне определенную форму.

Мысль о том, что сумма углов δ равна 360°, возникла не как некое допустимое предположение, общее утвер­ждение или вера, а как «интуиция»: структура фигуры позволила увидеть внутреннюю связь между замкнуто­стью и всеми углами δ.

Вслед за этим быстро последовали следующие дейст­вия:

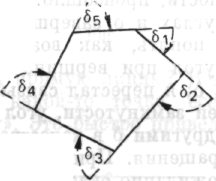
1) Было осознано, что должно произойти, если я шаг за шагом обойду фигуру, начиная с первой стороны пер­вой δ: для того чтобы замкнуть фигуру, я должен снова прийти к исходной прямой, совершив полный оборот. Сна­чала появилась общая идея ¹; затем она была реализова­на в виде последовательности действий: одна сторона угла δ₁ поворачивается на некоторый угол до совпадения с другой стороной, 2 параллельно переносится в положе­ние 3, поворачивается на угол δ₂ и т. д. Чтобы обойти всю фигуру, осуществляя замыкание, и снова перейти в положение 1, сторона должна совершить полный оборот в 360°.

¹ Позднее я нашел в одной книге замечание, принадлежащее физику Эрнсту Маху, который применил сходный метод. В ре­зультате суммирования б Мах тоже получил полный угол. Его

подход несколько отличается от нашего, угол разбивается не на R, δ, R, а на 2R, δ, что приводит к психологически иному способу образования полного угла.

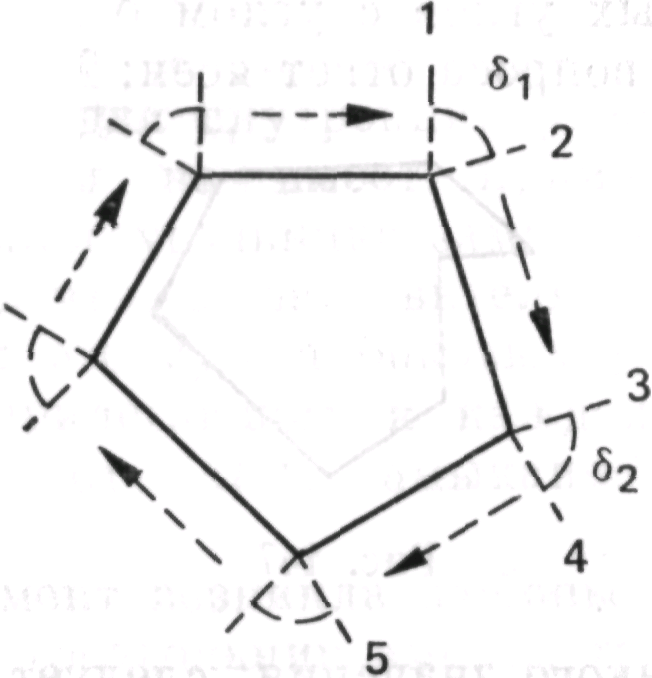
Рис. 143

2) Сразу после этого возникла следующая мысль: до­пустим, что стороны фигуры стремятся к нулю. Что про­изойдет в таком случае? Расстояние между соседними

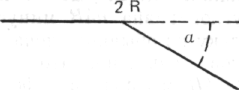
Рис. 144

параллельными сторонами боковых углов исчезнет, эти линии сольются в одну, совпадут также и вершины углов, и я получу именно ту картину, которая показана ниже: точку, которую окружает угловое пространство в 360°, построенное из углов d!

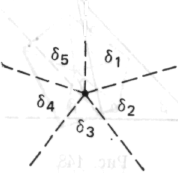
Рис. 146

3) Здесь возник следующий вопрос: а как обстоит дело с вогнутыми фигурами, которые не обладают ясной

структурой боковых углов с углом δ между ними? При такой постановке вопроса ответ ясен:

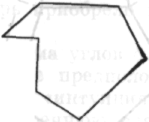
Рис. 147

это не имеет никакого значения; следует учесть, что сто­рона угла может поворачиваться в противоположную сто­рону, но все равно углы δ должны в сумме дать полный угол.

4) Обычный метод определения формулы для суммы внешних углов многоугольника теперь выглядел действи­тельно странным: «Сумма всех внутренних и полных внешних углов равна n · 4R...Σί+Σe = n · 4R. Следовательно, сумма внешних углов равна n4R минус сумма внутрен­них углов. Поскольку из обычного доказательства с помо­щью треугольников ¹ известно, что сумма внутренних углов равна n · 2R—4R, мы получаем формулу Σе = n · 4R— — (n ··2R—4R). Произведя вычитание, получаем: п · 4R—

¹ Обычно сумму углов треугольника — 180°, или 2R (два пря­мых угла), — получают, не учитывая того, что треугольник явля­ется замкнутой фигурой. Обычное доказательство для суммы внут­ренних углов многоугольника заключается в следующем: построй­те внутри многоугольника η треугольников так, чтобы каждая сто-

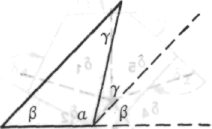
Рис. 148

рона многоугольника была основанием одного треугольника. Сум­ма углов всех треугольников равна n · 2R. Чтобы получить сумму внутренних углов многоугольника, вычтите из п · 2R смежные углы треугольников, которые располагаются вокруг средней точки. Сум­ма последних равна 4R. Следовательно: Σi = n ·2R—4R.

В этой формуле n · 2R есть результат вычитания n · 2R из n · 4R; 4R — это результат изменения знака члена —4R из формулы для внутренних углов. Величина чле­нов этой формулы не имеет прямого отношения к тому, как углы многоугольника замыкают фигуру ¹. Меж­ду тем я понял, что в действительности представляет собой n · 2R.+4R: это сумма боковых углов, то есть пар прямых углов, прилегающих к каждой стороне (n · 2R) плюс полный оборот (4R), замыкание, осуществляемое углами δ.

5) В этот момент возникла любопытная мысль: поче­му мы называем треугольник именно треугольником? По­чему мы не называем его, например, четырехугольником или шестиугольником? Мы, конечно, можем его так назы-

Рис. 150

вать, поскольку фактически в каждой точке на его сторо­нах находится угол. Но мы не считаем эти углы. Поче­му? Разве количество углов может быть любым? Нет.

¹ Конечно, член 4R в формуле для внутренних углов прямо связан с замкнутостью в том смысле, что вершины прилегающих

Рис. 149

друг к другу треугольников совпадают; но внутренняя связь меж­ду суммой углов самих треугольников и их замкнутостью не явля­ется столь отчетливой.

Теперь этот вопрос ясен: в этих точках на сторонах нет углов δ. Эти точки никак не связаны с изломом линии, ограничивающей фигуру, и с возвращением к ее началу, с замыканием многоугольника посредством вращения уг­лов δ.

6) А как обстоит дело с внутренними углами? Столк­нувшись теперь с этим вопросом, я снова не представлял себе, как можно на него ответить. И снова сначала воз­никла смутная идея: вокруг точки и фигуры имеется пол­ный угол 360°. Внутри фигуры находится... «отверстие»! И скоро все стало ясно: должен быть полный отрицатель­ный угол 360°: внутри боковые углы перекрываются. Ве­личина этого перекрытия представляет собой отрицатель­ный угол вращения, минус δ. Когда эта фигура замыка­ется, сумма таких углов должна составить полный отри­цательный угол в 360°.

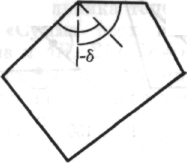
Рис. 151

Здесь читатель вправе задать вопрос, что же из всего этого следует. Та же самая формула, которая была из­вестна раньше, но она предстала теперь в новом свете: члены этой формулы приобрели прямое функциональное значение.

И такое понимание сразу же привело к озарению (ин­сайту): если боковые стороны и то или иное их число являются внешними, если существенным оказывается только вращение углов δ, то это относится к любой замк­нутой плоской кривой, к окружности, эллипсу, и т. д. ... (Я опускаю продолжение.)

7) Но проблема все еще не была окончательно реше­на. По мере того как она становилась ясной, возникало насущное требование: если такой ход рассуждения дей­ствительно имеет смысл, то тогда он должен иметь силу для любой замкнутой фигуры. Он должен быть справед­ливым для трехмерных многогранников, для четырехмер-

ных и n-мерных тел, вообще для всех замкнутых фигур... с необходимыми изменениями для неевклидового про­странства.

За шесть недель напряженной работы мне удалось по-настоящему понять трехмерные фигуры. (Годом поз­же я узнал, что один математик уже очень давно нашел формулу для многогранников, и все же я не хотел прой­ти мимо этого опыта, который привел меня к подлинному инсайту.) В течение этих недель проблема неизменно волновала меня, вызывала напряжение. Я изучал кон­кретные многогранники, например кубы, части кубов, некоторые пирамиды и т. д.; способы объединения телес­ных углов в полный телесный угол. За это время я зна­чительно развил в себе способность визуально представ­лять телесные углы и соединять их в воображении. Я не искал формулы методом проб и ошибок, не проверял гипотезы; я просто выяснял, что получится, если телес­ные углы воображаемого конкретного многогранника со­единятся в одной точке: например, как углы куба, све­денные в центр сферы, образуют полный телесный угол ¹, какие суммы образуют другие углы других многогранни­ков — частей куба, пирамид, параллелепипедов и т. д.

Бывали очень драматические моменты, как, напри­мер, когда один из моих друзей сказал мне: «Перестань принимать это так близко к сердцу. Задача неразрешима, так как сумма углов пирамиды меняется при изменении ее высоты. Точнее, она является функцией высоты».

8) Но процесс мышления продолжал развиваться. После огромных усилий решение для трехмерных тел

¹ Так же и в случае двух измерений угол при вершине квадрата является одной четвертью полного угла, причем все четыре угла делают его полным, или угол при вершине правильного шести­угольника составляет одну треть полного угла, три трети делают его полным.

Рис. 152

Вообще говоря, вводя понятие угла, следует рассматривать угол, как часть полного угла, или как часть вращения на полный угол (см. гл. 4. с. 162).

пришло ночью в полусонном состоянии. Хотя я не мог вспомнить, чтобы что-нибудь записывал, я утром обнару­жил на листе бумаги следующую формулу:

Σe =Σплоских углов +2 углов при вершинах+Σδ (= 1), где е обозначает внешний телесный угол. Возьмем плос­кость (а), согнем ее вдоль прямой линии (b); восстано­вим к каждой плоскости нормальную плоскость (с). Меж­ду нормальными «плоскими углами» (соответствующими боковым углам Н двумерных фигур) вы обнаружите «углы при вершинах» (с); согните эти углы в одной из точек (d), и вы получите δ. Чтобы многогранник был замкнутым, сумма углов δ должна составлять полный телесный угол!

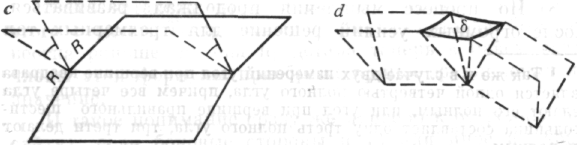
Рис. 153

Вскоре я понял, что то, что справедливо в частном случае «изгибания плоскости», имеет силу для всех телесных углов. Если вершины всех углов рассматривать как центр сферы, то углы δ, «полярные углы», должны заполнять сферу. С помощью этой идеи я получил формулу для многогранников. Затем было получено решение для сум­мы внутренних углов, основанное на идее объемного «от­верстия».

Последующие дни были посвящены строгим доказа­тельствам формул для сферы и т. д.

Я не буду описывать дальнейший ход моего мышле­ния. Здесь я прерву свой рассказ на том счастливом моменте, когда стала прозрачной внутренняя связь между замкнутостью и суммой углов многогранников и плоских фигур.

В заключение охарактеризуем основные этапы про­цесса мышления:

1. Ощущение существенной взаимосвязи структуры замкнутых фигур и суммы их углов и потребность ясно постичь эту связь.

2. Первичная идея целостной замкнутости и «углово­го пространства». Здесь произошло изменение цели: вме­сто того чтобы рассматривать внутренние углы, мы заня­лись вопросом о сумме внешних углов, смутно ощущая, что этот вопрос является структурно более простым. (Позднее эта мысль получила ясное подтверждение в хо­де мышления.)

3. Сосредоточение внимания на необходимом для замы­кания фигуры этапе привело к радикальному изменению понимания значения угла, к интуиции относительно «угла вращения δ»; это произошло в результате отделения того, что является структурно релевантным для осуществления замыкания, от того, что таковым не является.

4. Рассматривая углы δ как нечто целое, мы интуи­тивно поняли, что существует внутренняя связь между углами и замкнутостью. В отличие от простой суммы обычных углов все углы δ дают завершенную форму,
замкнутость, полный угол в 360°. На этом этапе произо­шла перегруппировка частей целого.

δ-части после отделения от боковых углов рассматри­вались как единое целое. Но даже если испытуемому на­чертить углы с уже проведенными дополнительными линиями, делящими каждый угол на три части, он может продолжать хаотически комбинировать углы обычным способом (при котором три части каждого отдельного угла оказываются равноценными, а сумма углов все еще состоит из обычных углов). Здесь производимая группи­ровка (отделение углов δ от структурно внешних боко­вых углов, не принимавших никакого участия в замыка­нии фигуры) направлялась задачей понять замкнутость фигуры. Концентрация внимания на углах δ и объедине­ние их в единое целое позволили найти структурный

перенос этого фактора (см. с. 227) на фоне внешних к структуре факторов: число боковых углов, обычных углов, сторон и вершин.

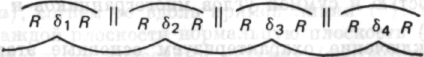
Рис. 154

5. Было дано подробное доказательство полученной интуитивно формулы. Уменьшая длины сторон до нуля, мы установили прямую связь между внешними углами и первоначальной идеей «углового пространства», окружаю­щего точку.

6. Возникла проблема, которая была затем решена; был найден принцип, применимый и в частном случае вогнутого многоугольника (см. с. 230).

7. Благодаря инсайту было осмыслено обычное дока­зательство, которое само по себе оставалось непонятным. Обычная формула обрела новый и более глубокий смысл: было обнаружено функциональное значение членов фор­мулы.

8. Затем был рассмотрен вопрос о внутренних углах. И снова вначале возникла глобальная идея целого — пред­ставление о цельном «отверстии», сумме отрицательных углов δ, равной 360°.

9. Расширилась область применимости полученного результата: было обнаружено, что он распространим на все замкнутые плоские фигуры. Благодаря инсайту ис­чезли ограничения, характерные для обычной точки зрения.

10. Мы почувствовали необходимость довести дело до конца: если в инсайте было обнаружено нечто фундамен­тальное, то найденное отношение должно выполняться также и для трехмерных фигур и т. д. Мы начинали с определения суммы телесных углов. Мы изучали сравни­тельно простые виды многогранников. Несмотря на труд­ности, мы в воображении объединяли углы и определяли их сумму. Вначале радикальное, общее решение казалось невозможным.

11. Решение пришло однажды ночью — это было

структурно ясное решение, как в гораздо более простом случае двухмерных фигур.

Самую важную роль в этом процессе играло стремле­ние постичь внутреннюю структуру задания. И снова мы увидели, какую роль в свете структурных требований иг­рают свойства целого, реорганизация, перегруппировка, постижение функционального значения частей в целом и т. д.

Каждый этап был частью единого последовательного хода мышления; полностью отсутствовали какие бы то ни было случайные действия, слепые пробы и ошибки.

Решение было найдено не сразу, процесс мышления протекал нелегко; это, очевидно, было вызвано тем, что в ходе мышления необходимо было преодолеть обычные, сами по себе ясные, сильные структурные факторы; а позднее, в случае многогранников, необходимо было на­учиться эффективно действовать в сложных проблемных ситуациях.

ГЛАВА 9

Открытие Галилея

Как Галилей открыл закон инерции и, таким образом, положил начало современной физике?

Вопрос о том, как в действительности мыслил Гали­лей, многократно обсуждался. Даже теперь это до конца не ясно. Очень трудно дать подробное описание его мыш­ления. Задача, стоявшая перед Галилеем, усугублялась тем, что существовали очень сложные понятия и теории о природе движения ¹. Исторические интерпретации неко­торых моментов отличаются друг от друга, это касается и вопроса о том, в какой степени старые концепции игра­ли роль в процессе мышления Галилея ².

Споры велись вокруг следующих вопросов: направля­лось ли мышление Галилея индукцией? Или дедукцией? Эмпирическими наблюдениями и экспериментом или же

¹ В частности, различались «естественное» и насильственное движения. Существовало понятие о необходимо уменьшающейся "vis impressa" (приложенной силе) и спекуляции о роли среды в задержке того момента, когда тело приходит в состояние покоя. Существовали определенные представления о «естественных» кру­говых движениях с постоянной скоростью и т. д.

² Читатели, которые интересуются историей развития теории, могут прочитать следующие труды: Wohlwill S. von. Die Entde­ckung des Beharrungsgesetzes.—"Zeitschrift für Völkerpsychologie und Sprachwissenschaft", 1883, Vol. XIV, S. 365—410; 1884, Vol. XV, S. 70—135; Mach E. Die Mechanik in ihrer Entwicklung. Leipzig. Brockhaus F. A., 1908, замечательные исследования Александра Койре «Этюды о Галилее» (1, II, III.Paris, Hermann, 1939) и, ко­нечно, прежде всего труды самого Галилея.

априорными предпосылками? Можно ли считать главной заслугой Галилея то, что он сделал качественные наблю­дения количественными?

Когда изучаешь литературу, — древние трактаты по физике и труды современников Галилея, — понимаешь, что одной из самых замечательных черт его мышления была способность достигать ясного структурного понима­ния на чрезвычайно сложном и запутанном фоне.

Я не буду пытаться здесь произвести историческую реконструкцию. Это потребовало бы тщательного обсуж­дения большого числа источников — а я не историк. К то­му же опубликованного исторического материала недо­статочно для психолога, которого интересуют особенности развития процесса мышления, обычно не получающие отражения в трудах ученых. К сожалению, мы не можем расспросить самого Галилея о том, как в действительно­сти развивался процесс его мышления. Мне бы, в част­ности, очень хотелось задать ему несколько вопросов по ряду пунктов.

Я постараюсь коротко изложить историю этого откры­тия и показать некоторые факторы и направления этого удивительного процесса, которые представляются мне наиболее существенными. Нижеследующая история явля­ется в некоторых отношениях психологической гипотезой, не претендующей на историческую точность, но я думаю, что она будет для нас весьма поучительной.

Я предлагаю читателю не только прочесть то, что я собираюсь рассказать, но и постараться поразмышлять вместе со мной.

I

Вот описание ситуации:

1. Если вы держите камень в руке, а потом отпустите его, то он упадет вниз. Старая физика утверждала: «Тя­желые тела ищут свое место, тяготеют к земле».

2. Если толкнуть какое-нибудь тело, например тележ­ку, или покатить по горизонтальной плоскости шар, то они придут в движение, некоторое время будут двигаться, а затем остановятся — вскоре, если я толкну их слабо, несколько позднее при сильном толчке.

Таков простейший смысл старого понятия «vis im­pressa». «Движущееся тело рано или поздно остановится,

если перестанет действовать приводящая его в движение сила». Разве это не так? Это очевидно.

3. Конечно, существуют некоторые дополнительные факторы, которые следует рассматривать в связи с вопро­сами движения, а именно величина объекта, его форма, поверхность, по которой он движется, наличие или отсут­ствие препятствий и т. д.

Итак, нам известно очень много фактов о движении. Они нам знакомы. Но понимаем ли мы их? Нам кажется, что понимаем. Понимаем ли мы, чем вызывается движе­ние? Видим ли мы здесь действие определенного прин­ципа?

Галилея не удовлетворяли эти знания. Он спросил се­бя: «Знаем ли мы, как действительно происходят такие движения?» Побуждаемый желанием понять главное, понять внутренние законы движения, Галилей сказал себе: «Мы знаем, что тяжелые тела падают, но как они падают? Падая, тело приобретает скорость. Ско­рость тем больше, чем большее расстояние проходит тело. Как изменяется скорость по мере движения тела?»

Обыденный опыт дает нам только смутную картину процесса. Галилей начал производить наблюдения и экс­периментировать, надеясь установить, что происходит со скоростью и управляется ли ее изменение законами, ко­торые можно понять. Его экспериментальные установки по сравнению с установками, которые позже разработали физики, были очень грубыми, по, проводя свои наблюде­ния и эксперименты, он пытался сформулировать и про­верить определенную гипотезу. Сначала он выдвинул ошибочную догадку, затем нашел формулу для ускорения падающего тела. Поскольку скорость падения столь ве­лика, что трудно установить ее точное значение, Галилей, желая более тщательно изучить вопрос, спросил себя: «Не могу ли я исследовать это более удобным способом? Шары скатываются по наклонной плоскости. Стану-ка я изучать шары. Разве свободное падение не является лишь частным случаем движения по наклонной плоскости, толь­ко под углом 90°, а не под меньшим углом?»

Изучая ускорение в различных случаях, он понял, что оно равномерно уменьшается с уменьшением угла накло­на: порядок угла соответствует порядку убывающего ускорения.

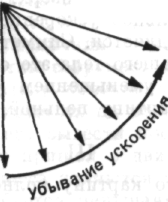
Рис. 155

Ускорение стало самым главным и центральным фак­тором, как только Галилей понял принцип, связывающий уменьшение ускорения с величиной угла.

II

Затем он внезапно спросил себя: «Но ведь это только половина картины? Разве то, что происходит, когда мы подбрасываем тело вверх или толкаем в гору шар, не является второй симметричной частью картины, которая, подобно отражению в зеркале, повторяет то, что у нас уже есть, и делает картину полной?»

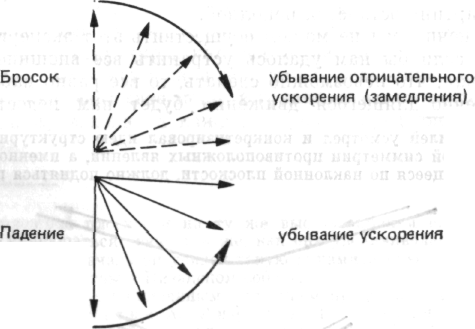
Рис. 156

Когда тело подбрасывают вверх, мы имеем не положи­тельное, а отрицательное ускорение. По мере движения тела вверх оно замедляется. Симметрично положительно­му ускорению падающего тела это отрицательное ускоре­ние уменьшается с уменьшением угла наклона. Такая симметрия делает картину цельной, законченной ¹

III

Но делает ли это картину полной? Нет. В ней есть пробел. Что произойдет в том случае, если плоскость бу­дет горизонтальной, угол равен нулю, а тело будет дви­гаться? Во всех случаях можно начинать с заданной скорости. Что тогда должно произойти в соответствии с такой структурой?

Ускоренное движение вниз и замедленное вверх пере­ходят с отклонением от вертикали... (положительное и отрицательное ускорения равны нулю)... в движение с достоянной скоростью?! Если тело движется по горизон­тали в заданном направлении, то оно будет продолжать двигаться с постоянной скоростью вечно, если только «внешняя сила не изменит его состояние движения.

Это противоречит старому утверждению, приведенно­му выше в пункте 2. Тело, движущееся с постоянной ско­ростью, никогда не придет в состояние покоя, если не будут действовать тормозящие силы, независимо от того, была ли сила, которая привела тело в движение, большой или малой. Какой удивительный вывод! Он явно проти­воречит всему, что мы знаем, и все же без него структур­ная картина останется неполной.

Конечно, мы не можем осуществить этот эксперимент. Даже если бы нам удалось устранить все внешние пре­пятствия, что невозможно сделать, то все равно наблюде­ние вечно длящегося движения будет нам недоступно.

¹ Галилей усмотрел и конкретизировал идею структурной ди­намической симметрии противоположных явлений, а именно: тело, скатывающееся по наклонной плоскости, должно подняться по про-

Рис. 157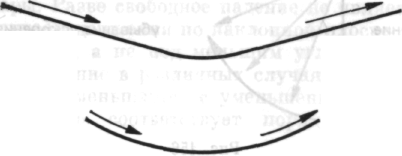

Рис. 158

Однако уменьшение ускорения ясно указывает на отсут­ствие изменения скорости в этом случае.

Взгляды Галилея получили подтверждение и заложи­ли основу для развития современной физики.

Современный читатель, конечно, знаком с этими взгля­дами. Я проиллюстрирую их на простом, всем известном примере. Труднее всего вывести поезд из состояния по­коя. Если поезд уже пришел в движение, то при усло­вии, что рельсы и колеса являются гладкими, для сохра­нения движения требуется меньшая сила, поезд движет­ся почти что сам по себе. Если мы теперь будем делать рельсы и колеса все более гладкими и будем наблюдать, как уменьшается сила, необходимая для движения, то графики, к нашему удивлению, покажут, что в случае идеально гладких колес и рельсов при отсутствии трения потребуется большие противодействующие силы, чтобы остановить поезд, привести его в состояние покоя ¹.

_______________

Каковы существенные элементы этого процесса?

Во-первых, желание выяснить, понять, что происхо­дит, когда тело падает или катится вниз; желание узнать, не кроется ли за этими явлениями какой-то внутренний принцип; желание рассмотреть эти явления при различных углах наклона.

Это центрирует мысль на ускорении. Эксперименталь­ная установка появляется в результате предположения, что, сосредоточившись на вопросе об ускорении, можно прийти к ясному пониманию структуры.

Различные случаи выступают как части хорошо упо­рядоченной структуры, которая делает явной зависимость между углами наклона и величиной ускорения. Каждый случай занимает свое место в группе, и мы понимаем, что то, что происходит в каждом случае, определяется этим местом.

тивоположной плоскости на ту же высоту, причем его скорость будет уменьшаться точно так же, как она увеличивалась при дви­жении вниз. Сначала он увидел такую динамическую симметрию в колебаниях люстры в Пизанском соборе.

¹ Ср. с очень упрощенным описанием процесса мышления Га­лилея в: Эйнштейн А., Инфельд Л. Эволюция физики. — Эйнштейн А. Собр. научных трудов, т. IV, М. «Наука», 1967, с. 357—543.

Во-вторых, эта структура рассматривается теперь как часть более широкого контекста: существует другая, до­полнительная часть, симметричная первой, с которой они образуют одно целое; эти две половины представляют собой две большие, соответствующие друг другу подгруп­пы, с положительным ускорением в одной и с отрица­тельным — в другой. Целостные свойства этих половин дополняют друг друга. Они рассматриваются с одной точ­ки зрения, в их структурной симметрии, в согласованной структуре целого.

В-третьих, оказывается, что в этой структуре сущест­вует критическое место — место горизонтального движе­ния. Это место должно существовать, иначе структура будет неполной. Ввиду этих требований горизонтальное движение выступает как случай, когда не происходит ни ускорения, ни замедления, — как случай движения с по­стоянной скоростью.

Таким образом, покой становится частным случаем движения с постоянной скоростью, случаем, когда отсут­ствует положительное или отрицательное ускорение. Покой и равномерное прямолинейное движение в гори­зонтальном направлении оказываются структурно эквива­лентными.

Конечно, Галилей использовал операции традицион­ной логики, такие, как индукция, умозаключение, форму­лировка и вывод теорем, а также наблюдение и искусное экспериментирование. (Одной из замечательных особен­ностей мышления Галилея было сочетание строгих рас­суждений, математических методов с использованием эксперимента для проверки теоретических идей или для поисков решения теоретических проблем.) Но все эти операции осуществляются на своем месте в общем про­цессе.

Сам процесс направляется перецентрацией, которая проистекает из желания добиться исчерпывающего пони­мания. Это приводит к трансформации, в результате ко­торой явления рассматриваются в составе новой, ясной структуры.

Переход от старого видения к новому привел к фун­даментальным изменениям значения понятий. Радикаль­но изменились места, роли и функции представлений о движении. Внутренние связи стали рассматриваться в совершенно новой структуре; была осуществлена новая

группировка, и была получена новая классификация дви­жений ¹.

Так, раньше покой и некоторые «естественные» кру­говые движения противопоставлялись другим видам дви­жения. Теперь покой и равномерное прямолинейное дви­жение стали рассматриваться как структурно равнознач­ные и противопоставлялись движениям с положительным или отрицательным ускорением.

Подъем и падение тел рассматриваются вместе как случаи ускорения, как симметричные части общей карти­ны. Свободное падение и свободное движение вверх рас­сматриваются как частные случаи общей группы движе­ний в каком-нибудь направлении.

Окончание движения больше не считается необходи­мым результатом уменьшающегося, прекращающегося действия vis impressa (приложенной силы). Теперь конец движения рассматривается совершенно иначе: движение прекращается вследствие внешнего трения.

Трение не является больше одним из многих факто­ров, которые следует учитывать при описании движения; теперь оно играет роль, противоположную роли инерции. В то время как раньше считали, что прямолинейное дви­жение прекращается независимо от наличия трения, благодаря естественному угасанию vis impressa, с новой точки зрения трение является основной причиной ограни­чения движения.

Сила выступает как нечто существенным образом определяющее ускорение.

Все представления приобретают новое значение бла­годаря той роли и функции, которую они выполняют в новой структуре.

Новые понятия открыли удивительную перспективу для понимания огромного числа явлений. Они позволили

¹ Для краткости я буду пользоваться некоторыми формулиров­ками, которые во всей полноте были найдены позже, но которые так или иначе подразумевались или уже намечались во взглядах Галилея. Сам Галилей был чрезвычайно осторожен в своих фор­мулировках.

Формулировка Галилея относится к горизонтальному движе­нию. Он также применял свой принцип к движению в других на­правлениях. Он не обобщил свой принцип до известного нам те­перь закона инерции, но это вскоре сделали другие. Мы не знаем наверное, сознавал ли он универсальный характер этого принципа.

совершенно по-новому рассматривать движение небесных тел. Впоследствии Ньютон описал эти движения как ре­зультат прямолинейного движения по инерции, с одной стороны, и ускоренного движения под действием силы тяжести — с другой.

_________

Продуктивные процессы часто имеют следующую при­роду: исследования начинаются с желания достичь под­линного понимания, найти более глубокие ответы на ста­рые вопросы. Определенная область в поле исследования становится критической, помещается в фокус; но при этом она не становится изолированной. Возникает новое, более глубокое структурное видение ситуации, предполагающее изменение функционального значения элементов, их но­вую группировку и т. д. Исходя из того, что требует ситуация в отношении критической области, мы приходим к разумному предсказанию, которое — подобно другим частям структуры — нуждается в прямой