Функционально полные системы функций алгебры логики
Лекция 5.
Систему элементарных ФАЛ от «n» переменных {f1, f2, … , fn} называют полной, если любая сколь угодно сложная ФАЛ F может быть выражена суперпозицией элементарных функций f1, f2, … , fn и переменных.
Примечание. Так как любая переменная может быть, в свою очередь, сложной функцией от других переменных, поэтому суперпозицией называют подстановку в функцию F вместо переменных других элементарных функций. Например, пусть исходная ФАЛ F равна: F = х1 + х2, при этом х1 = х2∙х3, а х2 = х4 + х5. Произведя суперпозицию элементарных функций и переменных, т.е. подставив в исходную функцию F вместо переменных х1 и х2 их аналитические выражении, получим:
F = х1 + х2 = х2∙х3 + х4 + х5 = (х4 + х5) ∙ х3 + х4 + х5.
Чтобы определить, какой набор ФАЛ обладает полнотой, рассмотрим прежде пять основных свойств функций алгебры логики.
Основные свойства ФАЛ.
1. Свойство сохранения нуля. Любая ФАЛ обладает этим свойством, если значение функция становится равным 0 при нулевых значениях всех переменных: f(x1 = 0, x2 = 0, … , xn = 0) = 0. Этим свойством обладают, например, элементарные логические функции И и ИЛИ. Действительно, используя значения функции на соответствующих наборах значений переменных из таблицы истинности элементарных функций И и ИЛИ, получим:
f(x1 = 0, x2 = 0) = х1∙х2 = 0∙0 = 0; f(x1 = 0, x2 = 0) = х1 + х2 = 0 + 0 = 0.
Необходимо при этом отметить, что функция отрицания (НЕ) этим свойством не обладает.
2. Свойство сохранения единицы. Любая ФАЛ обладает этим свойством, если значение функции становится равным 1 при единичных значениях всех переменных: f(x1 = 1, x2 = 1, … , xn = 1) = 1. Этим свойством обладают, например, элементарные логические функции И и ИЛИ. Действительно, используя значения функции на соответствующих наборах значений переменных из таблицы истинности элементарных функций И и ИЛИ, получим:
f(x1 = 1, x2 = 1) = х1∙х2 = 1∙1 = 1; f(x1 = 1, x2 = 1) = х1 + х2 = 1 + 1 = 1.
Необходимо при этом отметить, что функция отрицания (НЕ) этим свойством не обладает.
3. Свойство самодвойственности. Любая ФАЛ обладает этим свойством, если при инвертировании всех ее переменных происходит инвертирование функции, т.е. для функции f(x1, x2, … , xn), обладающей свойством самодвойственности, справедливо следующее: 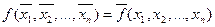 .
.
Понятие самодвойственной функции следует из понятия двойственной функции, которая получается из исходной функции в результате инвертирования этой функции после замены ее переменных на инверсные переменные. Так, например, двойственной по отношению к исходной функции f(x1, x2, … , xn) будет функция 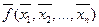 , которая в общем случае не равна исходной функции.
, которая в общем случае не равна исходной функции.
Проинвертируем обе части выражения, характеризующего основное свойство самодвойственной функции: 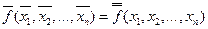 . Так как двойная инверсия любой функции не изменяет эту функцию, т.е. справедливо соотношение:
. Так как двойная инверсия любой функции не изменяет эту функцию, т.е. справедливо соотношение: 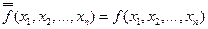 . Отсюда для самодвойственных функций справедливо и другое соотношение:
. Отсюда для самодвойственных функций справедливо и другое соотношение: 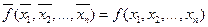 , т.е. самодвойственная функция это такая двойственная функция, которая равна исходной функции (двойственная по отношению к себе самой).
, т.е. самодвойственная функция это такая двойственная функция, которая равна исходной функции (двойственная по отношению к себе самой).
Свойством самодвойственности обладает функция отрицания (НЕ). Запишем аналитическое выражение для функции отрицания: f(x) = 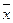 . Произведем инверсию переменной в исходной функции НЕ:
. Произведем инверсию переменной в исходной функции НЕ: 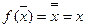 . Произведем инверсию исходной функции НЕ:
. Произведем инверсию исходной функции НЕ: 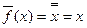 . Так как
. Так как 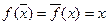 , то, следовательно, функция отрицания является самодвойственной функцией.
, то, следовательно, функция отрицания является самодвойственной функцией.
4. Свойство монотонности. Любая ФАЛ обладает этим свойством, если ее значение при возрастании номера набора значений переменных не убывает. Этим свойством обладают элементарные логические функции И и ИЛИ. Например, при номерах наборов, равных 0, 1 и 2, функция И не меняет своего нулевого значения. При большем номере набора, равном 3, значение функции И также изменяется и становится равным 1. При номере набора, равном 0, значение функции ИЛИ равно 1, при дальнейшем увеличении номера набора с 1 до 3 значение функции увеличивается и становится равным 1.
Функция отрицания не обладает эти свойством, так с увеличением номера набора, значение функции уменьшается: f(0) = 1; f(1) = 0.
5. Свойство линейности. Любая ФАЛ обладает этим свойством, если она может быть представлена полиномом первой степени вида:
f(x1, x2, … , xn) = 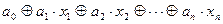 ,
,
где a0, a1, … , an – коэффициенты, равные 0 или 1.
Данным свойством обладает функция отрицания (НЕ), функция «сложение по модулю 2» и функция эквивалентности, которые могут быть представлены в виде полиномов первой степени: 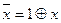 , х1
, х1 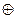 х2 = 0
х2 = 0 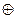 х1
х1 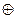 х2; х1 ~ х2 = 1
х2; х1 ~ х2 = 1 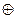 х1
х1 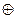 х2. Логические функции И, ИЛИ этим свойством не обладают.
х2. Логические функции И, ИЛИ этим свойством не обладают.
Так как при суперпозиции ФАЛ, имеющих основные свойства, получаются ФАЛ, которые также обладают основными свойствами, поэтому полная система функций не может состоять только из функций, обладающих основными свойствами, ибо в противном случае мы не сможем реализовать на них другие ФАЛ, не обладающие основными свойствами. Полная система ФАЛ должна включать в себя, хотя бы одну функцию, не обладающую одним из этих основных свойств.
Так, например, такие элементарные функции, как И-НЕ и ИЛИ-НЕ не обладают ни одним из указанных свойств, и каждая из них представляет собой функционально полную систему функций. Следовательно, любое дискретное устройство может быть построено только из логических элементов ИЛИ-НЕ или И-НЕ.
Функция запрета и константа 1 также образуют полную систему функций.
Базис и основные законы булевых функций.
Базисом называют полную систему ФАЛ. Минимальный базис состоит из такого набора элементарных функций, из которого без нарушения полноты нельзя исключить ни одной функции.
Наиболее распространенным базисом является полная система, содержащая три элементарные функции: И, ИЛИ И НЕ, которые являются основными логическими операциями алгебры логики (булевыми функциями). Этот базис называют основным базисом или булевым базисом.
Минимальный базис включает в себя две элементарные функции из основного базиса (ИЛИ и НЕ) или (И и НЕ).
Рассмотрим основные законы, которым подчиняются булевы функции.
1. Сочетательный (ассоциативный) закон. Данный закон гласит о том, что конечный результат (значение функции) не зависит от последовательности выполнения одноименных логических операций:
х1∙(х2∙х3) = (х1∙х2)∙х3; х1 + (х2 + х3) = (х1 + х2) + х3.
На рис. 20 представлен пример реализации сочетательного закона при использовании логической функции И для трех переменных.
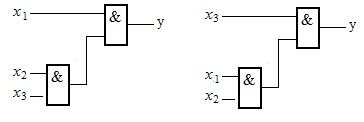
Рис. 20
2. Распределительный (дистрибутивный) закон. Согласно данному закону последовательность выполнения различных логических операций можно менять местами:
х1 ∙ (х2 + х3) = х1∙х2 + х1∙х3;
х1 + х2 ∙ х3 = (х1 + х2) ∙ (х1 + х3).
На рис. 21 представлен пример реализации распределительного закона при использовании логических функции ИЛИ и И для трех переменных.
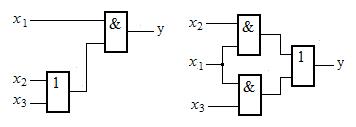
Рис. 21
3. Переместительный (коммутативный) закон. Согласно данному закону конечный результат логических операций не зависит от перемены мест слагаемых или сомножителей:
х1 ∙ х2 = х2 ∙ х1; х1 + х2 = х2 + х1.
4. Закон двойственности (правило де Моргана). Согласно правилу де Моргана инверсия дизъюнкции (операции логического сложения переменных) эквивалентна конъюнкции (логическому умножению) инверсных переменных:
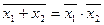 .
.
Аналогичным образом, инверсия конъюнкции переменных эквивалентна дизъюнкции инверсных переменных:
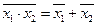 .
.
Согласно этому правилу, если известна исходная ФАЛ, например, f(x1, x2) = x1 + x2, то двойственная ей функция равна: 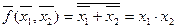 , т.е. элементарные функции ИЛИ и И являются двойственными функциями.
, т.е. элементарные функции ИЛИ и И являются двойственными функциями.
Для получения алгебраического выражения инверсной функции необходимо в исходной функции все переменные заменить на им инверсные, все знаки конъюнкции заменить на знаки дизъюнкции, и, наоборот, все знаки дизъюнкции заменить на знаки конъюнкции.
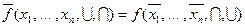 .
.
Рассмотрим пример получения инверсной функции:
Если исходная функция равна 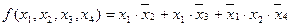 , то
, то
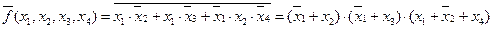 .
.
Наряду с основными законами в булевой алгебре логики действуют следующие соотношения, считающиеся аксиомами, истинность которых можно доказать, используя только таблицы истинности.
Для операций логического умножения (И).
1 ∙ х = х; 0 ∙ х = 0; х ∙ х = х; х ∙ 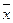 = 0.
= 0.
Для операций логического сложения (ИЛИ).
1 + 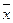 = 1; 0 + х = х; х + х = х; х +
= 1; 0 + х = х; х + х = х; х + 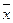 = 1.
= 1.
Для преобразования логических функций с целью их упрощения (минимизации) необходимо знать некоторые важные законы этого преобразования.
Закон поглощения переменных.
Закон поглощения переменных позволяет сократить количество одноименных переменных в ФАЛ. Он базируется на применении ряда аксиом алгебры логики и имеет две формы: конъюнктивную и дизъюнктивную.
Конъюнктивная форма закона поглощения. Суть этого закона заключается в том, что, если произвести логическое умножение функции от «n» переменных f(x1, x2, … , xn) с одной из ее переменных xi, то в исходной функции все одноименные переменные можно заменить логической 1, а инверсные по отношению к ним переменные заменить логическим 0: xi ∙ f(x1, x2, … , xi, 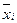 , … , xn) = xi ∙ f(x1, x2, … , 1, 0, … , xn).
, … , xn) = xi ∙ f(x1, x2, … , 1, 0, … , xn).
Пример: пусть исходная функция равна f(x1, x2) = (х1 +  ∙ х2), тогда согласно закону поглощения х1∙ f(x1, x2) = х1 ∙ (х1 +
∙ х2), тогда согласно закону поглощения х1∙ f(x1, x2) = х1 ∙ (х1 +  ∙ х2) = х1 ∙ (1 + 0 ∙ х2) = х1 ∙ (1 + 0) = х1 ∙ 1 = х1. Для наглядности применения аксиом алгебры логики в процессе последующего упрощения логического выражения соответствующие этим аксиомам знаки логических операций выделены более жирным шрифтом.
∙ х2) = х1 ∙ (1 + 0 ∙ х2) = х1 ∙ (1 + 0) = х1 ∙ 1 = х1. Для наглядности применения аксиом алгебры логики в процессе последующего упрощения логического выражения соответствующие этим аксиомам знаки логических операций выделены более жирным шрифтом.
Покажем поэтапно справедливость данного закона поглощения простым преобразованием логического выражения на основе применения основных законов и аксиом алгебры логики:
1. Исходное выражение: х1∙ f(x1, x2) = х1 ∙ (х1 +  ∙ х2).
∙ х2).
2. Применяя распределительный закон, получим:
х1 ∙ (х1 +  ∙ х2) = х1∙х1 + х1∙
∙ х2) = х1∙х1 + х1∙  ∙ х2.
∙ х2.
3. Для дальнейшего упрощения применяем лишь аксиомы:
х1 ∙ х1 + х1 ∙  ∙ х2 = х1 + 0 ∙ х2 = х1 + 0 = х1.
∙ х2 = х1 + 0 ∙ х2 = х1 + 0 = х1.
Как видим, в результате упрощения сократилось не только количество одноименных переменных и их инверсий, но и число выполняемых элементарных функций, а, следовательно, и число потребных логических элементов для реализации исходного выражения.
Если функцию f(x1, x2, … , xn) умножить логически на инверсную переменную 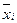 :
: 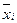 ∙ f(x1, x2, … , xn), то в функции f(x1, x2, … , xi,
∙ f(x1, x2, … , xn), то в функции f(x1, x2, … , xi, 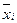 , … , xn) все переменные xi заменяются логическим 0, а
, … , xn) все переменные xi заменяются логическим 0, а 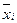 - логической 1:
- логической 1: 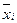 ∙ f(x1, x2, … , 0, 1, … , xn).
∙ f(x1, x2, … , 0, 1, … , xn).
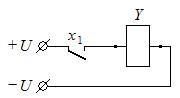
Рассмотрим примеры практического использования данного преобразования при анализе и синтезе релейно-контактных схем.
Допустим, в процессе синтеза получены две контактные схемы, представленные на рис. 22. Схема, представленная на рис. 22, а, реализует ФАЛ: 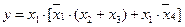 , а на рис. 22, б:
, а на рис. 22, б: 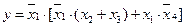 .
.
Согласно конъюнктивной форме закона поглощения:
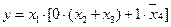 =
= 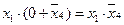 ;
;
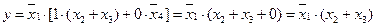
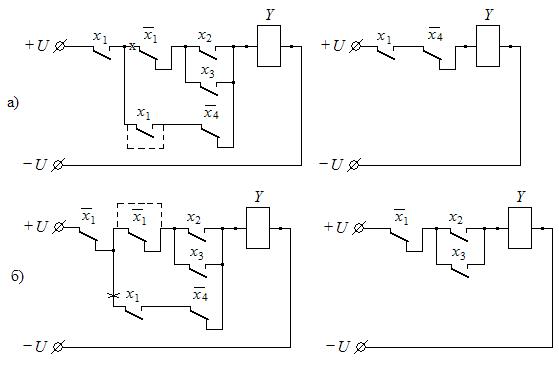
Рис. 22
Отсюда можно сделать следующий важный вывод: если последовательно с какой-либо контактной схемой включен одиночный контакт реле Х, то все одноименные по действию контакты этого реле, задействованные в схеме, можно закоротить, а все разноименные по действию контакты – исключить из схемы путем обрыва их цепи.
Для функции двух переменных конъюнктивная форма закона поглощения имеет вид:
х1 ∙ (х1 + х2) = х1 ∙ (1 + х2) = х1 ∙ 1 = х1;
х1 ∙ (  + х2) = х1 ∙ (0 + х2) = х1 ∙ х2;
+ х2) = х1 ∙ (0 + х2) = х1 ∙ х2;
 ∙ (х1 + х2) =
∙ (х1 + х2) =  ∙ (0 + х2) =
∙ (0 + х2) =  ∙ х2;
∙ х2;
 ∙ (
∙ (  + х2) =
+ х2) =  ∙ (1 + х2) =
∙ (1 + х2) =  ∙ 1 =
∙ 1 =  .
.
Дизъюнктивная форма закона поглощения. Суть этого закона заключается в том, что, если произвести логическое сложение функции от «n» переменных f(x1, x2, … , xn) с одной из ее переменных xi, то в исходной функции все одноименные переменные можно заменить логическим 0, а инверсные по отношению к ним переменные заменить логической 1:
xi + f(x1, x2, … , xi, 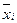 , … , xn) = xi + f(x1, x2, … , 0, 1, … , xn);
, … , xn) = xi + f(x1, x2, … , 0, 1, … , xn);
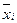 + f(x1, x2, … , xi,
+ f(x1, x2, … , xi, 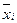 , … , xn) =
, … , xn) = 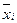 + f(x1, x2, … , 1, 0, … , xn);
+ f(x1, x2, … , 1, 0, … , xn);
Пример: пусть исходная функция равна f(x1, x2, х3) =  ∙ х2 ∙ х3, тогда согласно закону поглощения х1 + f(x1, x2, х3) = х1 +
∙ х2 ∙ х3, тогда согласно закону поглощения х1 + f(x1, x2, х3) = х1 +  ∙ х2 ∙ х3 = х1 + 1 ∙ х2 ∙ х3) = х1 + х2 ∙ х3.
∙ х2 ∙ х3 = х1 + 1 ∙ х2 ∙ х3) = х1 + х2 ∙ х3.
Для наглядности применения аксиом алгебры логики в процессе последующего упрощения логического выражения эти аксиомы подчеркнуты.
Покажем поэтапно справедливость данного закона поглощения простым преобразованием логического выражения на основе применения основных законов и аксиом алгебры логики:
1. Исходное выражение: х1 + f(x1, x2, х3) = х1 +  ∙ х2 ∙ х3.
∙ х2 ∙ х3.
2. Применяя распределительный закон, получим:
х1 +  ∙ х2 ∙ х3 = (х1 +
∙ х2 ∙ х3 = (х1 +  ) ∙ (х1 + х2 ∙ х3).
) ∙ (х1 + х2 ∙ х3).
3. Для дальнейшего упрощения применяем лишь аксиомы:
(х1 +  ) ∙ (х1 + х2 ∙ х3) = 1 ∙ (х1 + х2 ∙ х3) = х1 + х2 ∙ х3.
) ∙ (х1 + х2 ∙ х3) = 1 ∙ (х1 + х2 ∙ х3) = х1 + х2 ∙ х3.
Рассмотрим примеры практического использования данного преобразования при анализе и синтезе релейно-контактных схем.
Допустим, в процессе синтеза получены две контактные схемы, представленные на рис. 23. Схема, представленная на рис. 23, а, реализует ФАЛ: 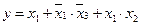 , а на рис. 23, б:
, а на рис. 23, б: 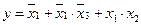 .
.
Согласно дизъюнктивной форме закона поглощения:
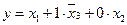 =
= 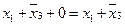 ;
;
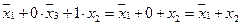 .
.
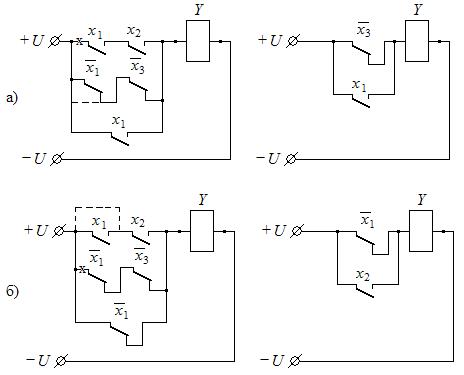
Рис. 23
Сформулируем правило упрощения контактной схемы при использовании дизъюнктивной формы закона поглощения.
Если последовательно какой-либо контактной схеме включен одиночный контакт реле Х, то все одноименные по действию контакты этого реле, задействованные в схеме, можно из схемы исключить путем обрыва их цепи, а все разноименные по действию контакты закоротить.
Для функции двух переменных дизъюнктивная форма закона поглощения имеет вид:
х1 + х1 ∙ х2 = х1 + 0 ∙ х2 = х1 + 0 = х1;
х1 +  ∙ х2 = х1 ∙ 1 + х2 = х1 + х2;
∙ х2 = х1 ∙ 1 + х2 = х1 + х2;
 + х1 ∙ х2 =
+ х1 ∙ х2 =  + 1 ∙ х2 =
+ 1 ∙ х2 =  + х2;
+ х2;
 +
+  ∙ х2 =
∙ х2 =  + 0 ∙ х2 =
+ 0 ∙ х2 =  + 0 =
+ 0 =  .
.
Задачи для самостоятельного решения
1. Перечислить элементарные функции алгебры логики из табл. 3, которые обладают свойством сохранения 0. Ответ: от f0 до f7.
2. Перечислить элементарные функции алгебры логики из табл. 3, которые обладают свойством сохранения 1. Ответ: все функции с нечетными индексами от f1 до f15.
3. Перечислить элементарные функции алгебры логики из табл. 3, которые обладают свойством самодвойственности. Ответ: f3, f5, f10 и f12.
4. Перечислить элементарные функции алгебры логики из табл. 3, которые обладают свойством монотонности. Ответ: f0, f1, f3, f7 и f15.
5. Составить таблицу истинности для функции 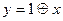 и определить, какой элементарной функции равносильна данная функция. Ответ:
и определить, какой элементарной функции равносильна данная функция. Ответ: 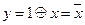 .
.
6. Используя дизъюнктивную форму закона поглощения упростить логическую функцию 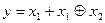 . Ответ:
. Ответ: 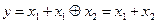 .
.
7. Используя конъюнктивную форму закона поглощения упростить логическую функцию 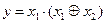 . Ответ:
. Ответ: 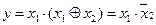 .
.
8. Используя соответствующий закон поглощения упростить приведенную ниже релейно-контактную схему.
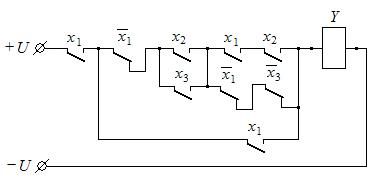
Ответ: