SUBJECT 2. Components of the computer. Peripherals (3 hours)
ТЕМА 2. Компоненты компьютера. Периферийные устройства (3 часа)
Boolean algebra. Logical operations
Булева алгебра. Логические операции
| The main provisions of the algebra of logic developed in the XIX century. English mathematician George Boole. The algebra of logic is also called Boolean algebra. | Основные положения алгебры логики разработал в XIX в. английский математик Джордж Буль. Алгебру логики называют также булевой алгеброй. |
| In Boolean algebra, binary variables are distinguished and switching functions. Binary variables can take two values: 0 and 1. They are also called logical or Boolean variables and are denoted by x1, x2, x3, ... | В булевой алгебре различают двоичные переменные и переключательные функции. Двоичные переменные могут принимать два значения: 0 и 1. Они называются также логическими или булевыми переменными и обозначаются символами х1,x2,х3,... |
| Switching function (PF) depends on the binary variables. They, like arguments, can take only two values: 0 or 1. PF is also called logical or Boolean functions. We denote the Fermi surface in the form f (x1, x2, x3, ...). specifying arguments in parentheses, either as y1, y2, y3, .... | Переключательные функции (ПФ) зависят от двоичных переменных. Они, как и аргументы, могут принимать лишь два значения: 0 или 1. ПФ называют также логическими или булевыми функциями. Будем обозначать ПФ в виде f(х1,x2,х3,...). указывая в скобках аргументы, либо в виде y1,y2,y3,... . |
| Set variables - is a set of binary variables, each of which may be 0 or 1. If the number of arguments (independent variables) PF equals n (i.e. x1, x2, x3, ... xn), then there exists two different combinations of these variables t. e. set. | Набор переменных — это совокупность значений двоичных переменных, каждая из которых может быть равна 0 или 1. Если число аргументов (независимых переменных) ПФ равно n (т.е. х1,x2,х3,...xn), то существует 2 различных сочетаний этих переменных, т. е. наборов. |
| Arbitrary FS can be expressed in the form of a function of binary variables (or other PF) using a limited number of elementary logic functions. Consider these features. Logical negation (NOT function). The logical negation of a variable x is such PF f1 (x), which has a value of 1 when x = 0 and 0 when x = 1. PF is not indicated in the form and read: «f1 is (equivalent to) not x" | Произвольная ПФ может быть выражена в форме функции от двоичных переменных (либо от других ПФ) с помощью ограниченного числа элементарных логических функций. Рассмотрим эти функции. Логическое отрицание (функция НЕ). Логическим отрицанием переменной х называется такая ПФ f1(x), которая имеет значение 1, когда x = 0 и значение 0, когда х= 1. ПФ НЕ обозначается в виде 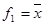 и читается: «f1 есть (эквивалентно) не х» и читается: «f1 есть (эквивалентно) не х» |
Truth table of the logical function NOT Таблица истинности логической функции НЕ
|
Logical multiplication (conjunction). The conjunction of the two (or any other number) variables x1 and x2 is set to 1 only on the set in which all the variables are 1. On the other sets, this function is set to 0. The table is a truth table of the conjunction of two variables x1 and x2. PF conjunction is denoted as 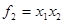 and read: «f2 is (equivalent to) x1 and x2». To denote the conjunction can use symbols and read: «f2 is (equivalent to) x1 and x2». To denote the conjunction can use symbols  or &. Conjunction is also called a function and, as it is set to 1 only if the first and second arguments are irrelevant 1. or &. Conjunction is also called a function and, as it is set to 1 only if the first and second arguments are irrelevant 1. | Логическое умножение (конъюнкция). Конъюнкция двух (или любого другого числа) переменных х1 и х2 принимает значение 1 только на наборе, в котором все переменные имеют значения 1. На остальных наборах эта функция имеет значение 0. Таблица представляет собой таблицу истинности конъюнкции двух переменных х1 и x2. ПФ конъюнкция обозначается в виде 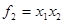 и читается: «f2 есть (эквивалентно) х1 и x2». Для обозначения конъюнкции можно использовать символы и читается: «f2 есть (эквивалентно) х1 и x2». Для обозначения конъюнкции можно использовать символы  или &. Конъюнкция называется также функцией И, так как она имеет значение 1, только если первый и второй аргументы имеют значения 1. или &. Конъюнкция называется также функцией И, так как она имеет значение 1, только если первый и второй аргументы имеют значения 1. |
| Logical multiplication (conjunction) Логическое умножение (конъюнкция) |
Logical addition (disjunction). The disjunction of two (or any other number) variables x1 and x2 is 0 only on the set, in which all variables have a value of 0. If at least one of the variables is equal to 1, the function will be set to 1. PF disjunction is written in the form 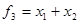 and read: «f3 is (equivalent to) x1 or x2». Also the + character, used for disjunction symbol V. Since the function of the disjunction is set to 1 if the first and second arguments are set to 1, the operation is also called disjunction OR operation. and read: «f3 is (equivalent to) x1 or x2». Also the + character, used for disjunction symbol V. Since the function of the disjunction is set to 1 if the first and second arguments are set to 1, the operation is also called disjunction OR operation. | Логическое сложение (дизъюнкция). Дизъюнкция двух (или любого другого числа) переменных х1 и х2 имеет значение 0 только на наборе, в котором все переменные имеют значение 0. Если хотя бы одна из переменных равна 1, функция будет иметь значение 1. ПФ дизъюнкция записывается в виде 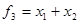 и читается: «f3 есть (эквивалентно) х1 или x2». Кроме символа + , для дизъюнкции употребляется символ V. Так как функция дизъюнкции имеет значение 1, если первый или второй аргументы имеют значение 1, операция дизъюнкции называется также операцией ИЛИ. и читается: «f3 есть (эквивалентно) х1 или x2». Кроме символа + , для дизъюнкции употребляется символ V. Так как функция дизъюнкции имеет значение 1, если первый или второй аргументы имеют значение 1, операция дизъюнкции называется также операцией ИЛИ. |
| Logical addition (disjunction). Логическое сложение (дизъюнкция). |
The negation of the conjunction (AND operation - NOT). This feature is produced by negating the result obtained in step I. From the comparison table it is clear that the PD and - is the negation (NOT operation) conjunctions. PF and - written in the form 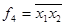 . . | Отрицание конъюнкции (операция И — НЕ). Эта функция образуется путем отрицания результата, получаемого при выполнении операции И. Из сравнения таблиц видно, что ПФ И — НЕ является отрицанием (операцией НЕ) конъюнкции. ПФ И — НЕ записывается в виде |
| The negation of the conjunction (AND operation - NOT). Отрицание конъюнкции (операция И — НЕ). |
The negation of the disjunction (OR operation - NOT). This operation formed by the negation of the result obtained in the performance or operation. From the comparison table shows that the PF or - is the negation (NOT operation) disjunction. PF OR - NOT written as 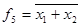 | Отрицание дизъюнкции (операция ИЛИ — НЕ). Эта операция образуется путем отрицания результата, полученного при выполнении операции ИЛИ. Из сравнения таблиц видно, что ПФ ИЛИ — НЕ является отрицанием (операцией НЕ) дизъюнкции. ПФ ИЛИ — НЕ записывается в виде 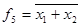 |
| The negation of the disjunction (OR operation - NOT). Отрицание дизъюнкции (операция ИЛИ — НЕ). |
XOR (unequal operation or modulo two). This function has the value 1 to the variable sets in which the number of ones is odd. This operation is recorded for the two variables in the form 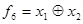 / Operation unequal expressed through operations NOT, AND, OR, in the form / Operation unequal expressed through operations NOT, AND, OR, in the form 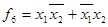 . . | ИСКЛЮЧАЮЩЕЕ ИЛИ (операция НЕРАВНОЗНАЧНОСТЬ или СЛОЖЕНИЕ ПО МОДУЛЮ ДВА). Данная функция имеет значение 1 на тех наборах переменных, в которых число единиц нечетно. Эта операция записывается для двух переменных в виде 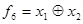 / Операция НЕРАВНОЗНАЧНОСТЬ выражается через операции НЕ, И, ИЛИ в виде / Операция НЕРАВНОЗНАЧНОСТЬ выражается через операции НЕ, И, ИЛИ в виде 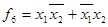 . . |
| XOR (unequal operation or modulo two). ИСКЛЮЧАЮЩЕЕ ИЛИ (операция НЕРАВНОЗНАЧНОСТЬ или СЛОЖЕНИЕ ПО МОДУЛЮ ДВА). |
An exclusive OR operation - not (equivalent to). Equivalent to the function is a negation of the exclusive OR operation. This operation has the value 1 to the sets of variables to contain an even number of units. This operation is recorded for two variables in the form of 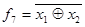 . An exclusive OR operation - not expressed in terms of operations NOT, AND, OR, in the form . An exclusive OR operation - not expressed in terms of operations NOT, AND, OR, in the form 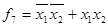 . . | Операция ИСКЛЮЧАЮЩЕЕ ИЛИ — НЕ (РАВНОЗНАЧНОСТЬ). Функция РАВНОЗНАЧНОСТЬпредставляет собой отрицание операции ИСКЛЮЧАЮЩЕЕ ИЛИ. Данная операция имеет значение 1 на тех наборах переменных, которые содержат четное число единиц. Эта операция записывается для двух переменных в виде 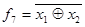 . Операция ИСКЛЮЧАЮЩЕЕ ИЛИ — НЕ выражается через операции НЕ, И, ИЛИ в виде . Операция ИСКЛЮЧАЮЩЕЕ ИЛИ — НЕ выражается через операции НЕ, И, ИЛИ в виде 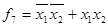 . . |
| An exclusive OR operation - not (equivalent to). Операция ИСКЛЮЧАЮЩЕЕ ИЛИ — НЕ (РАВНОЗНАЧНОСТЬ). |
| | |
| | |
| | |
| | |
| HOME WORK |
| Given the binary numbers A and B (the data in the table). Perform operations: - denial - Logical addition - Denial or - Logical multiplication - Denial and - XOR - Denial of the exclusive-OR | Даны двоичных числа А и В (данные в таблице). Выполнить операции: - отрицание - логическое сложение - отрицание ИЛИ - логическое умножение - отрицание И - исключающее ИЛИ - отрицание исключающего ИЛИ |
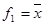 и читается: «f1 есть (эквивалентно) не х»
и читается: «f1 есть (эквивалентно) не х» 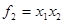 and read: «f2 is (equivalent to) x1 and x2». To denote the conjunction can use symbols
and read: «f2 is (equivalent to) x1 and x2». To denote the conjunction can use symbols  or &. Conjunction is also called a function and, as it is set to 1 only if the first and second arguments are irrelevant 1.
or &. Conjunction is also called a function and, as it is set to 1 only if the first and second arguments are irrelevant 1. 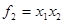 и читается: «f2 есть (эквивалентно) х1 и x2». Для обозначения конъюнкции можно использовать символы
и читается: «f2 есть (эквивалентно) х1 и x2». Для обозначения конъюнкции можно использовать символы  или &. Конъюнкция называется также функцией И, так как она имеет значение 1, только если первый и второй аргументы имеют значения 1.
или &. Конъюнкция называется также функцией И, так как она имеет значение 1, только если первый и второй аргументы имеют значения 1. 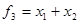 and read: «f3 is (equivalent to) x1 or x2». Also the + character, used for disjunction symbol V. Since the function of the disjunction is set to 1 if the first and second arguments are set to 1, the operation is also called disjunction OR operation.
and read: «f3 is (equivalent to) x1 or x2». Also the + character, used for disjunction symbol V. Since the function of the disjunction is set to 1 if the first and second arguments are set to 1, the operation is also called disjunction OR operation. 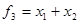 и читается: «f3 есть (эквивалентно) х1 или x2». Кроме символа + , для дизъюнкции употребляется символ V. Так как функция дизъюнкции имеет значение 1, если первый или второй аргументы имеют значение 1, операция дизъюнкции называется также операцией ИЛИ.
и читается: «f3 есть (эквивалентно) х1 или x2». Кроме символа + , для дизъюнкции употребляется символ V. Так как функция дизъюнкции имеет значение 1, если первый или второй аргументы имеют значение 1, операция дизъюнкции называется также операцией ИЛИ. 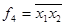 .
. 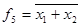
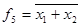
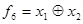 / Operation unequal expressed through operations NOT, AND, OR, in the form
/ Operation unequal expressed through operations NOT, AND, OR, in the form 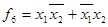 .
. 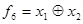 / Операция НЕРАВНОЗНАЧНОСТЬ выражается через операции НЕ, И, ИЛИ в виде
/ Операция НЕРАВНОЗНАЧНОСТЬ выражается через операции НЕ, И, ИЛИ в виде 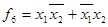 .
. 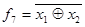 . An exclusive OR operation - not expressed in terms of operations NOT, AND, OR, in the form
. An exclusive OR operation - not expressed in terms of operations NOT, AND, OR, in the form 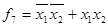 .
. 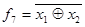 . Операция ИСКЛЮЧАЮЩЕЕ ИЛИ — НЕ выражается через операции НЕ, И, ИЛИ в виде
. Операция ИСКЛЮЧАЮЩЕЕ ИЛИ — НЕ выражается через операции НЕ, И, ИЛИ в виде 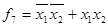 .
. 